0 引言

    扩频通信技术是一种十分重要的抗干扰通信技术，具有抗干扰能力强、可进行多址通信、隐蔽性好、抗多径衰落等多种优势，在移动通信、卫星导航、信号侦查与探测等领域都得到了广泛的应用^[1]。扩频序列是影响扩频通信系统性能的重要因素，近些年来，混沌序列由于其初值敏感性、类随机特性、数量众多等性质^[2]在扩频通信系统中得到了广泛的应用,目前研究比较深入的有改进型Logistic映射^[3]、Chebyshev映射^[4]、Tent映射^[5]等。上述映射虽然拥有良好的类随机特性和相关性，迭代公式简单，工程上易于实现，但是均为一维单级迭代映射，结构简单，生成的混沌序列复杂度不够高，通过相空间重构、反向迭代等方法被破译的可能性较大^[6]。因此本文提出了一种通过迭代级联混沌映射构造新型扩频序列的方法，将迭代方程的输入输出值在不同的单级混沌映射间切换，在反复迭代的过程中改善了系统的动力学特性，扩展了系统的密钥空间，增加了混沌序列的复杂度，更有利于提高扩频通信系统的安全保密性。

1 迭代级联混沌映射

1.1 迭代级联混沌映射的提出

    改进型Logistic混沌映射定义为^[3]：

    当初始值x₀∈(-1，1)，分型参数μ=2时，系统处于混沌状态，并且为满映射。

    Chebyshev混沌映射定义为^[4]：

    初始值x₀∈(-1，1)，ω为映射的阶数，当ω=2ⁿ时，系统处于混沌状态。

    考虑到改进型Logistic混沌映射和Chebyshev混沌映射具有相同的取值范围和相同的概率密度分布函数，为了提高混沌系统的复杂度和安全性，可将上述两种映射通过迭代级联的方法构造出一种新型混沌映射，将一个混沌映射的输出作为另一个混沌映射的初值并进行反复迭代^[7]。每次迭代在两种单级混沌映射中随机选择一种，当映射总迭代次数为N时，整个混沌系统共有2^N种不同的混沌映射组合方式，大大提高了混沌系统的密钥空间。由于每次迭代的初值在不同的混沌映射中切换，有效提高了相空间轨道的模糊性，进一步提高了混沌系统的复杂度、保密性、安全性。当每次迭代都选择同一种混沌映射时，迭代级联混沌映射将退化为普通的单级映射，此时改进型Logistic混沌映射和Chebyshev混沌映射成为新型混沌映射的两种特殊形式。

    鉴于迭代级联混沌映射组合方法多达2^N种，难以逐一分析，本文针对其中一种映射交替迭代的特殊情况进行分析。新型混沌映射数学表达式如下：

    给定初值x₀后，迭代公式在两种单级混沌映射中交替切换，每次迭代的结果由两种单级混沌映射的相关参数和迭代次数共同决定，大大提高了混沌系统的复杂度和安全性，下面对该新型混沌映射的性质进行分析。

1.2 新型混沌映射遍历性分析

    分岔图可以清楚地反映出分形参数μ与混沌映射离散数值分布的关系^[6]。图1中给出了改进型Logistic混沌映射和新型混沌映射的分岔图。

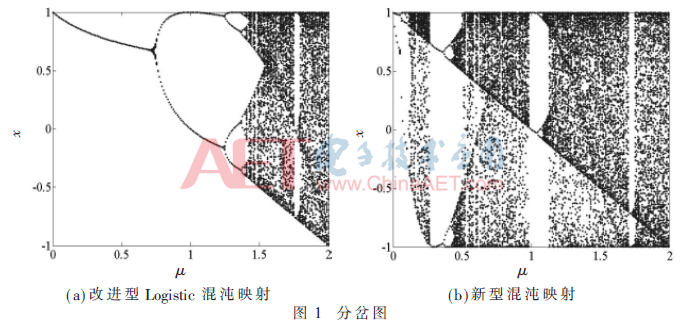
    由图1可以看出对于改进型Logistic混沌映射，只有在分形参数μ=2时，迭代结果才会映射在整个[-1，1]区间，这种状态被称作满映射状态。当分形参数取其他数值时，混沌序列迭代数值范围缩小，数值分布集中，系统的遍历性和随机性降低。而本文提出的新型混沌映射扩展了满映射状态的分布区间，使分形参数μ的可选取范围大大增加，这进一步扩展了混沌系统的密钥空间，系统安全性、保密性能得到提升。

2 混沌序列性能分析

2.1 混沌序列的数字量化

    为了将混沌映射产生的实值序列应用到扩频通信系统中，需要对实值序列进行数字量化处理，将实值序列转化为二进制序列。二值量化法是一种最常见的数值量化方法，其核心思想是寻找一个判决门限T，将序列数值与门限T比较，方法如下式：

    二值量化法原理简单，但是判决门限T的选择将影响到混沌扩频序列的平衡性，扩频序列的平衡性反映了二进制序列中1与-1数量的均匀程度，其定义式为:

其中U与V分别表示序列中1与－1的数目，N表示序列长度。混沌序列的平衡性与载波抑制度有密切的关系，低平衡性的混沌序列会导致直扩系统的载漏增大，将破坏扩频系统保密性、抗干扰和抗侦破的能力^[8]。选择合适的判决门限，提高序列的平衡性对提升扩频通信系统的性能有重要的意义。下面对迭代级联混沌映射的判决门限进行分析。

    由图1可以看出，虽然保证数值分布为满映射的分形参数μ的取值范围大大增加，但当分形参数μ=2时混沌映射数值分布更加均匀，有更良好的随机性，因此在新型混沌映射模型式(5)中，设置相关参数μ=2，ω=4，迭代次数10 000次，对其数值在[-1，1]区间上的分布情况进行统计，统计结果如图2所示。

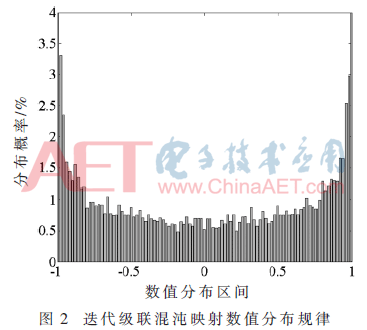
    由图2可以看出在给定参数下，新型混沌映射的数值分布规律与构成新型混沌映射的两个子映射的概率密度分布函数类似，两边高、中间窄，近似关于x=0成轴对称分布，因此可以选取T=0作为新型混沌映射的判决门限。

2.2 平衡性分析

    下面分析新型混沌序列二值化后的平衡性。随机选取50个不同的初值，计算平衡性的平均值并绘出曲线，结果如图3所示。可以看出随着序列的长度增加，序列的平衡性越来越好，新型混沌序列的平衡性优于改进型Logistic混沌序列和Chebyshev混沌序列。

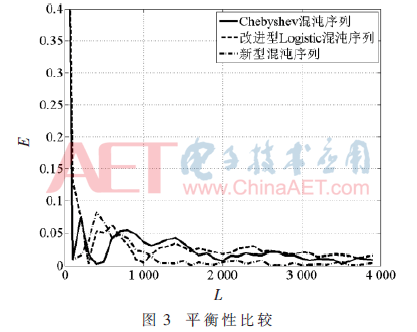
2.3 复杂度分析

    有限长序列的复杂度是指它与随机序列的相似程度，可以在一定程度上反映出通信系统的保密性能和抗截获性能。传统伪随机扩频序列的复杂度通常采用Berlekamp-Massey算法进行衡量，但该算法是一种计算线性复杂度的算法，有较大的局限性，并不适合用来衡量混沌序列的复杂度^[9]。文献[10]提出了一种通过近似熵（ApEn）算法来衡量混沌扩频序列复杂度的方法，该算法通过描述序列维数增加时混沌轨道的分离程度来衡量混沌序列的复杂度，物理意义清晰，计算方法简单易实现，其计算步骤如下：

    (1)混沌序列长度为N，以序列值域为样本得到N点数据a(1)，a(2)，…，a(N)。

    (2)构造m维向量组：

    (5)定义近似熵(ApEn)为：

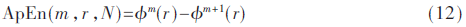
    ApEn数值越大，混沌序列的复杂度越高。上述参数中m通常取1或2，r通常取0.1~0.25倍样本数据的标准差^[9]。

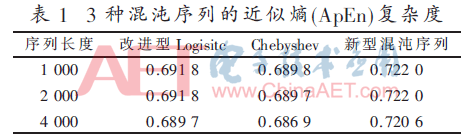
    下面对经过二值化的新型混沌序列、Logistic混沌序列、Chebyshev混沌序列三者的ApEn进行仿真计算，计算参数为N分别取1 000、2 000、4 000，r取0.12，m取2，计算结果如表1所示。由表1可以看出新型混沌序列的复杂度最高，改进型Logisitc混沌序列次之，Chebyshev混沌序列复杂度最低。这也证实了本文提出用迭代级联混沌映射构造的新型混沌序列确实具有更高的复杂度，更有利于提高通信系统的保密性和抗截获性。

2.4 相关性分析

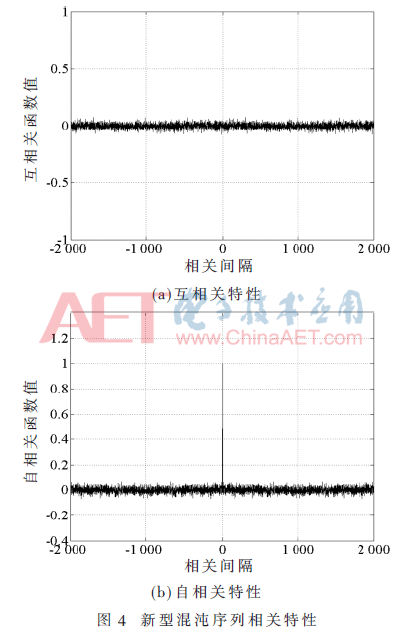
    相关性是衡量扩频序列性能的重要指标，与扩频通信系统的抗干扰能力和抗多址能力密切相关。理想的扩频序列应该具备类似白噪声一样尖锐的自相关函数，和处处为零的互相关函数^[11]。理论上无限长混沌序列可以满足上述性质，但在实际应用中混沌序列不可能取到无限长，要经过截短处理后才能使用，这在一定程度上破坏了混沌序列的相关特性。图4显示一个初值为x=0.1，参数设定为μ=2，ω=4，序列长度为2 000的新型混沌序列自相关函数值和互相关函数值的分布情况，从图中可以看出新型混沌序列的自相关函数值有尖锐的相关峰，自相关函数旁瓣值和互相关函数值均接近于零,表明新型混沌序列有良好的相关性能。

3 扩频通信仿真

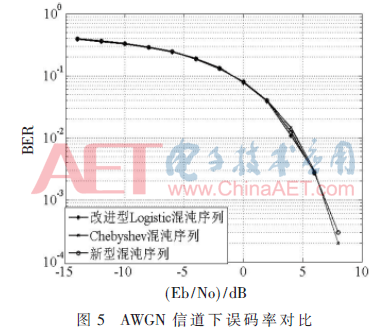
    为了进一步验证本文提出的新型迭代级联混沌扩频序列的性能,通过MATLAB软件对3种混沌序列进行扩频通信仿真。仿真条件设定序列码长1 024，信噪比取值范围是[-15 dB，10 dB]，调制方式为BPSK，混沌序列参数选取μ=2、ω=4，每种混沌序列随机选取1 000个初值设并计算误码率平均值,经过AWGN信道后误码率曲线如图5所示。由图5可以看出3种混沌序列在理想高斯白噪声信道下误码率曲线相互交叉，基本重合，误码率性能相当。

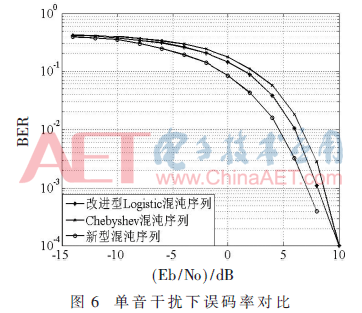
    下面考虑AWGN信道中加入干扰信号的情况，仿真条件不变，在高斯信道中加入单音干扰信号，误码率曲线如图6所示，图中可以看出新型混沌序列的误码率明显低于改进型Logistic混沌序列和Chebyshev混沌序列，说明新型混沌序列相对于其他两种混沌序列具有更强的抗干扰能力。

4 结论

    本文在改进型Logistic混沌映射和Chebyshev混沌映射的基础上提出了一种新型迭代级联混沌映射。其组合方式多样，迭代方程由多个参数共同决定，有效提高了混沌系统的复杂度和安全性。通过对该映射进行遍历性分析，发现其满映射分布区间更广，随机性能更好。对新型混沌序列二值化判决门限的选取进行了分析，仿真对比验证3种混沌序列的平衡性、复杂度和相关性，结果表明，本文提出的新型混沌序列复杂度高，具有良好的相关性和平衡性，抗干扰能力更强，更加适用于扩频通信系统中。

参考文献

[1] 暴宇，李新民.扩频通信技术及应用[M].西安：西安电子科技大学出版社，2011.

[2] 刘嘉兴，何世彪.混沌测控的概念、特性与实现[J].飞行器测控学报，2011，30(1)：1-5.

[3] 王亥，胡健栋.改进型Logistic-Map混沌扩频序列[J].通信学报，2007，28(2)：134-140.

[4] 雷利华，马冠一，蔡晓静，等.基于Chebyshev映射的混沌序列研究[J].计算机工程，2009，35(24)：1-3.

[5] 刘金梅，张卫，丘水生.一种改善Tent混沌序列随机性的方法[J].计算机工程，2012，38(24)：10-12.

[6] 李双鑫，王驰，李广喆，等.一种新型的二级分段Logistic混沌映射及其性能分析[J].东北师大学报(自然科学版)，2014，45(4)：82-87.

[7] 李长庚，周家令，孙克辉，等.基于M序列同步的混沌扩频通信系统研究与仿真[J].系统仿真学报，2009,21(4)：1198-1201.

[8] 罗冬梅.混沌序列特性分析及同步技术研究[D].重庆：重庆大学，2011.

[9] 蔡觉平，李赞，宋文涛.一种混沌伪随机序列复杂度分析法[J].物理学报，2003，52(8)：1871-1876.

[10] PINCUS S M.Approximate entropy as a measure of system　complexity[J].Proceedings of the National Academy of Science，1991，88(6)：2297-2301.

[11] 余振标，冯久超.一种混沌扩频序列的产生方法及其优选算法[J].物理学报，2008，57(3)：1409-1415.