0 引言

    随着人们对于高速率、高质量无线通信需求的飞速增长，尽可能高的频谱效率和能量效率成为新一代无线通信系统的核心竞争指标。2008年首次提出并不断发展成熟的非正弦时域正交调制方法^[1]（Nonsinusoidal Orthogonal Modulation in Time and Domain，NOTDM），利用椭圆球面波函数的高时频能量聚集性来提高系统的功率利用率，采用时域正交、频域混叠的正交脉冲组实现多路信息传输，进而提高了系统的频谱效率，是极具应用前景的非正弦波通信新体制。

    椭圆球面波函数（Prolate Spheroid Wave Function，PSWF）已经被证明是时频域能量聚集性最佳的信号形式^[2-4]，但其高能量聚集性是以系统频带利用率的降低为代价的，时间带宽积c越大，λ越大，PSWF能量聚集性越好，系统频带利用率越低^[5-8]，如何优化设计正交椭圆球面波函数脉冲组参数是决定系统性能的重要因素。文献[9]给出了基于PSWF的正交脉冲设计的详细方法，但是只给出了频谱交叠度为50%的情况。文献[10]讨论了不同频谱交叠度时系统频带利用率提升的速度，但是缺少对不同频谱交叠度情况下调制信号能量聚集性和频谱特性的讨论。另外，时间带宽积是影响脉冲组性能的另一个典型参数，但是尚未发现国内外文献对不同时间带宽积条件下系统性能变化进行详细的讨论和分析。

    本文在非正弦时域正交调制方法的基础上，着眼于如何确定合适的PSWF脉冲组参数，重点分析了频谱交叠度和时间带宽积等典型脉冲参数对时域正交PSWF脉冲组的正交性、时频能量聚集性，以及用于信息传输时，已调信号的功率谱特征、系统的频带利用率等方面的影响，进而以脉冲组的功率利用率和频带利用率为主要指标，提出了时域正交PSWF脉冲组的参数优选方案。仿真结果表明，综合各项性能指标所设计的时域正交PSWF脉冲组参数优选方案，在保证调制信号具有高能量聚集度的同时，系统保持较高的频带利用率和较低的实现复杂度。

1 频谱交叠度对正交PSWF脉冲组的影响分析

    非正弦时域正交调制方法利用一组时域正交、频谱交叠且时频能量聚集性较优的PSWF脉冲并行调制后叠加成一路信号进行传输，可以少量脉冲实现系统频带利用率的快速提高。接收端依靠脉冲间的良好正交性，通过相关解调和检测完成多脉冲的分离和调制信息的获取。

    当多路PSWF信号并行传输时，由于PSWF满足双正交性^[11]，可以在不引入脉冲间干扰的前提下，允许各路PSWF信号在时域上相互叠加，在频域上频谱相互交叠。为探究频谱交叠度对正交PSWF脉冲组的影响，在频谱交叠度分别为45%、50%、55%、60%条件下，定性分析了时域正交PSWF脉冲组的性能指标，并比较了用于信息传输时通信系统的性能指标。

1.1 频谱交叠度对脉冲组时域特性的影响分析

    选取频带范围划分的子频段个数k=4，每个子频带带宽B₀=100 Hz，时间带宽积为c=4π，脉冲的持续时间为T_s=40 ms。具体参数设置如表1所示。

    根据时域正交PSWF脉冲组设计的一般方法可知，PSWF的时间带宽积c与脉冲个数m满足关系式：m=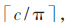因此在同一子频段内，所取PSWF脉冲的个数为m=4，脉冲组的正交脉冲个数为N=m×k=16。

    这里以正交PSWF脉冲组的最大互相关值作为检验脉冲组正交性能的标准，按照表1的参数设计在不同频谱交叠度下脉冲组的正交性能如表2所示。

    从表2中可以看出，频谱交叠度的大小基本不影响脉冲组的最大互相关值，即不影响脉冲组的正交性能。可见，依据表1的参数设置得到的正交PSWF脉冲组都具有较好的正交性能。

1.2 频谱交叠度对脉冲组频域特性的影响分析

    下面利用表1的参数设置设计的正交PSWF脉冲组传输信息时，对已调信号的功率谱特性进行分析。已调信号的归一化功率谱如图1所示。

    已调信号的归一化功率谱特性如表3所示。

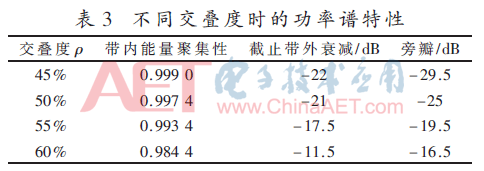
    从图1及表3中可以看出，当频谱交叠度ρ较小时，调制信号的带内能量聚集性较大，功率谱旁瓣功率和截止带外衰减都较高；随着频谱交叠度的增大，调制信号的带内能量聚集性逐渐降低，功率谱旁瓣功率和截止带外衰减也在频谱交叠度较大时大幅降低，在交叠度为ρ=70%的情况下，带内能量聚集性下降到92%，功率谱旁瓣衰减降到-12.5 dB，而截止带外衰减甚至降到-3.5 dB，极大地降低了系统的功率利用率。可见，随着频谱交叠度ρ的增大，调制信号的带内能量聚集性逐渐变差，其功率谱特性也急剧变差。

1.3 频谱交叠度对系统特性的影响

    下面对不同频谱交叠度时的频段划分方式下所设计的时域正交PSWF脉冲组采用非正弦时域正交调制，用于信息传输时，对通信系统无码间干扰条件下的单位频带利用率进行理论分析。

    在子频段时间带宽积为c时，同一子频段选用的PSWF脉冲个数m==T_sB₀，子频段划分个数为k、子频段带宽为B₀时，则采用非正弦时域正交调制，利用时域正交PSWF脉冲组实现信息的多路并行传输时，信息传输的总速率为：

    按照表1的参数设置得到的正交PSWF脉冲组用于信息传输时，系统的单位频带利用率和峰均功率比如表4所示。

    从表4中可以看出，当频谱交叠度较小时，系统的频带利用率较低，随着频谱交叠度的增大，系统的单位频带利用率不断增大。在频谱交叠度不小于50%时，系统的频带利用率可已达到2 Baud/Hz。另外，随着频谱交叠度的增大，系统的峰均功率比不断减小。

    综合考虑各性能指标，频谱交叠度50%时，所设计的时域正交PSWF脉冲组在保证已调信号具有较好的能量聚集性(即具有较好的功率利用率)的前提下，正交PSWF脉冲信号具有较小的边值幅度，随着子频段划分数的增加，系统的单位频带利用率可达2 B/Hz，同时不会给系统带来较高的复杂度。

2 时间带宽积对正交PSWF脉冲组的影响分析

    由上一节的分析可知，在频谱交叠度为50%或55%的情况下，正交PSWF脉冲组的性能较好，因此，下面在频谱交叠度为50%时，针对时间带宽积c分别为3π、4π、5π、6π的情况，通过仿真分析所设计时域正交PSWF脉冲组的性能指标，并根据低复杂度、高频带利用率和高功率利用率的系统特点，确定正交脉冲组的优化设计方法。

2.1 时间带宽积对脉冲组频域特性的影响分析

    为了便于分析比较，下面给出仿真实例。在通信频段1 000 Hz~1 250 Hz、带宽250 Hz内设计时域正交PSWF脉冲组，划分的子频段个数k=4，每个子频带带宽B₀=100 Hz，频谱交叠度为ρ=50%，其他具体参数设置如表5所示。

    在子频段时间带宽积不同时的已调信号的功率谱如图2所示。

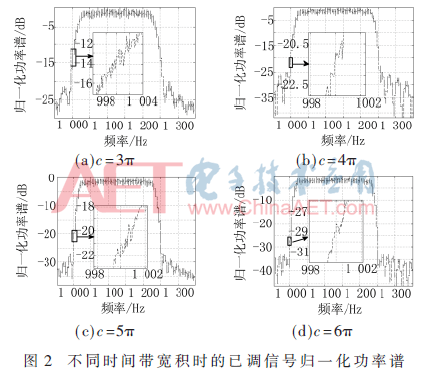
    子频段时间带宽积不同时的功率谱特性如表6所示。

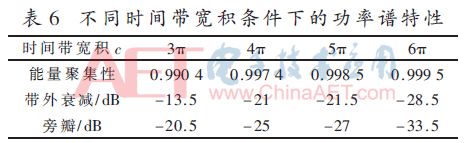
    如表6所示，当时间带宽积c=2π时，仅有92.20%的能量集中在频段1 000 Hz~1 250 Hz内；当时间带宽积c=3π时，仅有99.04%的能量集中在频段1 000 Hz~1 250 Hz内；而当时间带宽积c分别为4π、5π、6π时，分别有99.74%、99.85%、99.95%的能量集中在给定的频段范围内。可见随时间带宽积的增大，调制信号的带内能量聚集性不断提高，系统的功率利用率也不断提高。

    从图2及表6中可以发现，在时间带宽积c较小时，调制信号功率谱旁瓣功率较低，且其截止带外衰减也较低，仅为-2.5 dB，极大地影响了系统的功率利用率。随着时间带宽积c的增大，功率谱旁瓣功率及其截止带外衰减功率逐渐提高，系统的功率利用率也不断提高。

2.2 时间带宽积对系统性能的影响分析

    下面采用非正弦时域正交调制，对不同时间带宽积条件下所设计的时域正交PSWF脉冲组用于信息传输时，对通信系统无码间干扰条件下的单位频带利用率进行分析。

    交叠度50%时，系统的单位频带利用率为：

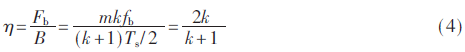
其中，k为子频段数，m为每个子频段的脉冲个数，T_s为脉冲持续时间，f_b为单个脉冲的信息传输速率。在频谱范围和划分子频带个数相同的情况下，子频段的时间带宽积c越小，每个子频段选取的脉冲数m越少，系统的复杂度越小。

    依据表5的参数设置得到的正交PSWF脉冲组用于信息传输时，系统的单位频带利用率和峰均功率比如表7所示。

    从表7中可以看出，当时间带宽积c较小时，系统的峰均功率比很小，而且正交脉冲的数量较少，因此用于时域正交调制时，系统的复杂度较小，但随着时间带宽积的增大，每个子频带选取的正交脉冲个数增多，导致系统的峰均功率比急剧增大，并大大增加了时域正交调制系统的复杂度。

    从各项性能指标综合考虑来看，当时间带宽积为c=4π时，所设计的时域正交PSWF脉冲组在保证已调信号具有较好的能量聚集性(即具有较好的功率利用率)的前提下，脉冲信号具有较小的边值幅度，同时不会给系统带来较高的复杂度。

3 基于参数优选的功率谱特性优化研究

    由分析可知，随着子频段时间带宽积c的增大，脉冲调制信号的旁瓣衰减功率逐渐降低，其功率谱特性逐渐变好。同时，正交化后单阶脉冲的频谱范围有所扩大，且随着脉冲数的增加，脉冲旁瓣高度逐渐增大。因此，可以通过增大总时间带宽积c，同时减少参与正交化的脉冲个数N的方式来优化调制信号的功率谱特性。

    设计带宽B=250 Hz，频谱范围为1 000~1 250 Hz，码元时间宽度T_s=40 ms，总时间带宽积为c=πBT=10π，子频带划分数k=4，频谱交叠度ρ=50%。

    为了方便比较不同脉冲个数时的调制信号功率谱特性，每个子频带上的脉冲个数分别选取m=2、3、4，这样参与正交的脉冲个数分别为N=8、12、16，因此可以得到的脉冲组参数设置如表8所示。

    按照表8中的参数设置，在总时间带宽积c=10π的情况下，N=8、12、16时的调制信号的功率谱在给定频段内分布较均匀，其旁瓣功率分别为-33.5 dB、-27.5 dB和-25 dB，其截止带外衰减功率分别为-30 dB、-24 dB、-22 dB。仿真结果显示，在此参数设置下，分别有99.95%、99.81%和99.74%的能量集中在给定的频段范围内。可见随着脉冲个数的减少，功率谱旁瓣和截止带外衰减逐渐减小，调制信号的能量聚集性有所提高。

    另外，经过计算发现，在N=16时系统的单位频带利用率为η=1.6 Baud/Hz，N=12时为η=1.2 Baud/Hz，N=8时为η=0.8 Baud/Hz。可见虽然上述仿真通过减少正交脉冲个数可以改善调制信号的功率谱，但这是以降低系统的频带利用率为代价的，是在功率谱特性和系统性能之间折衷权衡的一种参数设置方法。

    依然按照上节的基本参数设置：设计带宽B=250 Hz，频谱范围为1 000~1 250 Hz，子频带划分数k=4，频谱交叠度ρ=50%。

    为了方便比较不同脉冲个数时的调制信号功率谱特性，码元持续时间分别取T_s=40 ms、44 ms、48 ms，这样总时间带宽积为c=πBT=10π、11π、12π。在正交脉冲个数N=16的情况下，总时间带宽积分别为c=10π、11π、12π时，调制信号的功率谱旁瓣为-25 dB、-33 dB和-37.5 dB，其截止带外衰减分别为-22 dB、-26 dB、-29 dB，且此时调制信号的带内能量聚集性分别为0.997 4、0999 95和0.999 9，可见随着时间带宽积的增大，调制信号的截止带外衰减功率逐渐降低，带内能量聚集性增高，系统的功率利用率明显提高。

    但在此情况下，c=10π时的系统单位频带利用率为η=1.6 Baud/Hz，c=11π时为η=1.45 Baud/Hz，c=12π时为η=1.33 Baud/Hz，可见虽然增大时间带宽积可以降低调制信号的截止带外衰减，改善其功率谱特性，提高系统的功率利用率，但这种方法也是以牺牲系统的单位频带利用率为代价，是在脉冲组功率谱特性和系统特性实现折衷的参数设置方法。

    综上所述，通过脉冲组的参数优选，增大时间带宽积c和减少正交脉冲个数N，都可以优化调制信号功率谱特性，但同时降低了单位频带利用率，是以牺牲系统特性为代价的折衷措施。

4 结论

    本文以频谱交叠度和时间带宽积为典型参量，分析脉冲参数对信号正交性和用于信息传输时对已调信号的带内能量聚集性和功率谱旁瓣的影响，以及对系统的频带利用率、峰均功率比和复杂度的影响。综合考虑系统实现复杂度、频带利用率和功率利用率，给出了ρ=50%和c=4以及ρ=55%和c=4π这两种时域正交PSWF脉冲组的参数优选措施。仿真结果表明，综合各项性能指标所设计的时域正交PSWF脉冲组参数优选方案在调制信号能量聚集度达到99.7%的同时，系统极限频带利用率达到2 Baud/Hz，且保持了较小的实现复杂度。该优选方案取得了功率利用率和频带利用率的良好折衷，在固体系统中可以根据实际需求对参数进行调整，以达到系统性能最优化。

参考文献

[1] 王红星，赵志勇，刘锡国，等.非正弦时域正交调制方法[P].中国：ZL 2008 10159238.3，2011.

[2] SLEPIAN D，POLLAK H O.Prolate spheroidal wave functions，Fourier analysis，and uncertainty-I[R].The Bell System Technical Journal，1961：43-46.

[3] LANDAU H J，POLLAK H O.Prolate spheroidal wave functions，Fourier analysis，and uncertainty-III：the dimension of the space of essentially time- and band-limited signals[R].The Bell System Technical Journal，1962:1295-1336.

[4] KEDAR K，NICHOLAS G.Sampling theory approach to prolate spheroidal wave functions[J].Journal of Physics，2003，36(39)：10011-10021.

[5] KAROUI A.Unidimensional and bidimensional prolate spheroidal wave functions and applications[J].Journal of the Franklin Institute，2011，348(7)：1668-1694.

[6] Wei Liying，KENNEDY R A，LAMAHEWA T A.An optimal basis of band-limited functions for signal analysis and design[J].IEEE Transactions on Signal Processing，2010，58(11)：5744-5755.

[7] OSIPOV A，ROKHLIN V.On the evaluation of prolate spheroidal wave functions and associated quadrature rules[J].Appliedand Computational Harmonic Analysis，2014，36：108-142.

[8] SANCTIS M D，CIANCA E，ROSSI T.Waveform design solutions for EHF broadband satellite communications[J].IEEE Communications Magazine，2015，53(3)：18-23.

[9] 赵志勇，王红星，李洪烈，等.非正弦波通信时域正交椭圆球面波脉冲设计方法[J].电子与信息学报，2009，31(12)：2912-2916.

[10] 赵志勇，王红星，刘锡国，等.正交椭圆球面波函数脉冲调制方法[J].电子与信息学报，2012，34(10)：2331-2335.

[11] PARR B，CHO B，WALLACE K.A novel ultra-wideband pulse design algorithm[J].IEEE Communication Letters，2003，7(5)：219-221.