0 引言

    越来越多的研究人员致力于网络流量特征的研究，现有的网络流量中都能检测到自相似特性。赫斯特指数(Hurst index，H指数)是描述自相似特性的唯一特征参数，它能刻画网络业务量突发的剧烈程度，影响网络业务量建模的准确度。

    赫斯特指数估计方法的研究开始于国外，起初学者大多数集中在对R/S法(Rescaled Range，R/S)的研究上，后来提出了一些新的H指数估计方法和应用。MARCIN M提出了基于p-variation的估计方法^[1]，这种方法可以估计单分形布朗运动的H指数。BLYTHE D A J^[2]将H指数的估计方法运用到脑电图的分析当中，演示了信号噪声比例在H指数估计中的影响。国内的学者也对H指数的估计方法进行了大量的研究和应用。张广兴^[3]将H指数估计方法运用于多尺度下的IP网络流量特征分析与研究。徐凌^[4]提出了一种基于Haar小波的Hurst参数估计方法，比传统估计方法的精度有所提高。目前比较常用的自相似业务量估计方法有R/S分析法、聚类方差法、周期图法、Whittle法^[5]、小波分析法。其中Whittle法需要在已知序列的谱密度形式的情况下才能对序列进行准确估计，而真实网络业务量的谱密度形式往往是未知的，所以本文只对其他4种方法进行研究。

1 自相似过程及其数学特性

1.1 自相似过程的定义

1.2 自相似过程的特征

    赫斯特效应：Hurst参数是自相似过程的唯一参数，当H=0.5表明时间序列是随机的，0.5<H<1表明时间序列具有自相似性，网络业务量的H值一般在0.75附近。

1.3 分形高斯噪声模型

    分形高斯噪声^[9](Fractal Gaussian Noise，FGN)是目前最为广泛使用的一种自相似模型。FGN序列的自相关函数为：

2 Hurst指数估计法及修正办法

2.1 R/S估计法

2.1.1 原理

    对于具有自相似性的序列X有：

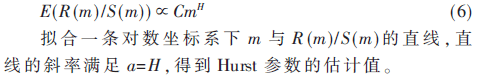
2.1.2 R/S修正办法

    在实际应用中m值的设定关系到算法的运算时间和算法的精度。图1是m值的个数与估计方法运算一次所需要的时间关系，自相似业务量长度为2¹⁶。

    从图1可以看出，m的个数的增加带来了运算时间大幅增加，因此m值的个数应该固定，即m的个数不随自相似业务量序列的长度的增加而增加。同时仿真结果表明R/S法的估计精度不受m的取值个数影响，实验数据见表1。可以通过适当减少m值的个数提高运算速度。本文的仿真都是在自相似业务量序列长度为2¹⁶，Hurst参数取0.6、0.7、0.8、0.9这4个值的情况下仿真出来的结果。相对误差是分别对设定的4个Hurst参数估计后求得的值求平均的结果。

    表2是m的最小值与算法的相对误差关系，表2的仿真数据可以看出随着m的最小取值的增加估计法的相对误差降低了2.42%，说明可以通过提高m的最小值的取值来提高R/S法的估计精度，N是自相似业务量序列长度。

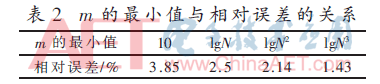
    表3是m的最大值与估计法的相对误差之间的关系，最小值取lgN³，从表3可以看出m值的最大取值偏大时R/S法的估计相对误差较小。

    综上所述，对于R/S法的修正办法有：(1)m值的个数固定，避免因自相似业务量序列的增加带来的运算量的大幅增加；(2)增大m值的最小取值可以使R/S估计法的相对误差减少2.32%；(3)增大m的最大取值，这种方式也可以提高估计法的精度。

2.2 聚类方差法

2.2.1 原理

    绘制对数坐标系下Vn与m的曲线，H=1+a/n，a为斜率，从而可以计算Hurst参数的值。当n=1时对应算法为绝对值法，当n=2时对应算法为方差时间法。

2.2.2 聚类方差修正办法

    同R/S法一样，聚类方差法中m值的选取也可以直接影响估计精度和运算速度。图2是m值的个数与估计方法运算一次所需要的时间之间的关系。

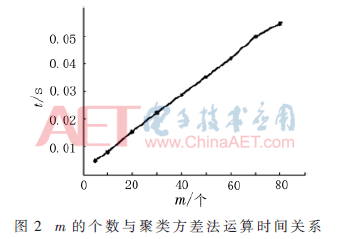
    从图2可以看出随着m的个数的增加，运算一次估计法所需的时间也大幅增加，所以m值的个数应该固定。表4中等间隔取值就是m在最大值和最小值之间等间隔地取值，不等间隔的取值就是在最小值与最大值之间呈对数取值。表4的仿真结果表明m以不等间距的方式来取值比等间距取值的精度高。从表4也可以看出当m的个数在40左右时精度较高。

    表5是在m的最小值取不同值时得到的估计误差，N表示自相似业务量序列的长度。从表5可以看出随着m的最小值的增大，估计法的精度逐渐下降。

    表6是在m的最小值取10的情况下讨论最大值对精度的影响，从表6可以看出m值的最大取值偏小时聚类方差法的估计精度高，即m的最大值的选择应该适当偏小，当取N/500时精度最高。

    综上所述，对于聚类方差法的修正办法有：(1)m取值的个数固定，避免序列的增加带来运算量的大幅增加；(2)m值不等间隔选取，可以使相对误差降低3个百分比；(3)降低m值的最小取值和最大取值，可以使相对误差降低8个百分比。

2.3 周期图法

2.3.1 原理

    周期图法^[10]是一种信号功率谱密度估计方法。对于观测到的时间序列X={X(k)，k=1，2，3，…，N}，其周期图由下式定义为：

2.3.2 周期图法修正办法

    选择原点附近的点来拟合曲线对周期图法是很重要的，选择过多的点I(λ)与|λ|^1-2H失去了正比关系，选择的点过少会影响精度。从表7中可以看出，选择靠近原点15%左右的点进行拟合得到的估计精度是最高的。

    因此可以总结出对周期图法的修正办法：适当选择靠近原点15%的点进行曲线拟合，这种情况下周期图法的估计误差最小，精度最高。

2.4 小波法

2.4.1 原理

    给定一时间序列X={X(i)，i=1，2，3，…，N}，对其进行二进制小波变换可以得到信号的近似系数d_x(j，k)^[11]。

    若X(i)为二阶平稳过程，则：

其中 C(H，Ψ)是依赖H和Ψ的常数，j是尺度系数。从式(12)可以得出在对数坐标系下拟合一曲线，H=(1+a)/2，a是曲线的斜率。

2.4.2 小波法修正办法

    影响小波估计法精度的因素有两点：(1)小波基的选择；(2)尺度的选择。表8对比了4种小波基在H指数估计当中对精度的影响。Harr小波就是Daubechies小波中阶数为1的情况。

    从表8中可以看出，小波基和尺度j的选择会影响小波估计法的精度，采用Harr小波基进行小波估计在尺度j=5时小波估计的相对误差最低为0.25%。

    因此，可以总结出两点小波估计法的修正办法：(1)选择Harr和Biorthogonal小波基；(2)选合适的尺度，j=5左右情况下估计法的相对误差最小。

3 结论

    本文针对目前广泛使用的4种自相似业务量估计方法提出了详细的修正的办法。通过设置不同的Hurst参数以及长度为2¹⁶的业务量序列来测试修正前后估计方法的精度，结果表明采用修正办法可以降低各个估计方法的相对误差，提高估计方法的估计精度，其中R/S法的相对误差降低到1.43%，聚类方差法的相对误差降低到1.30%，周期图法和小波估计法的相对误差降低了一个数量级，小波估计法的相对误差降低到了0.25%。

    下一步的工作：(1)研究这些方法的抗噪性能，改进估计方法，提高鲁棒性；(2)将估计方法采用硬件实现，用于对网络流量的实时检测。

参考文献

[1] MARCIN M，JAKUB K，JUSTYNA W.Estimation and testing of the Hurst parameter using p-variation[J].Journal of Physics A：Mathematical and Theoretical，2013，46(32)：2589-2593.

[2] BLYTHE D A J，HAUFE S，M?譈LLER K R，et al.The effect of linear mixing in the EEG on Hurst exponent estimation[J].Elsevier，2014，99(1)：377-387.

[3] 张广兴.多尺度下的IP网络流量特征分析与研究[D].长沙：湖南大学，2011.

[4] 徐凌，刘嘉焜，李亮.自相似网络流量Hurst指数估计算方法[J].科学技术与工程，2013，13(20)：5848-5854.

[5] 宋春凤.通信网络流量的自相似研究[D].长春：吉林大学，2015.

[6] 李稚春.网络时延的自相似性研究[J].物联网技术，2015，38(4)：38-40.

[7] KOROLKO M，SAHINOGLU Z，NIKOVSKI D.Modeling and forecasting self-similar power load due to EV fast chargers[J].IEEE Smart Grid，2015，12(9)：508-519.

[8] YOON I，JEON J，PAIK J.Multi-frame example-based super-resolution using locally directional self-similarity[J].Consumer Electronics，2015，12(2)；2-4.

[9] DELIGNIERES D.Correlation properties of (Discrete) fractional Gaussian noise and fractional brownian motion[J].Mathematical Problems Engineering，2015，10(8)：1-3.

[10] 赵彦仲，吴立文.Hurst指数估计方法的比较和研究[J].计算机工程与应用，2014，50(16)：1-3.

[11] 赵彤洲，李德华，吴量，等.基于多尺度小波分析的长程相关性研究[J].华中科技大学学报，2015，43(10)：487-488.