0 引言

    近二十年来，随着计算机多媒体技术的普及和应用，出现了大规模数字图像库，基于内容的图像检索技术因此得到发展。它是使用同一种方法分别从查询图像和目标图像中提取特征，通过特征对比输出最终检索结果^[1]。纹理是一种基本视觉和全局特征，它反映了图像中不依赖于颜色和亮度的同质现象，在基于内容的图像检索中已经得到广泛的应用^[2]。纹理分析方法分为统计方法、结构方法、模型方法和频谱方法。

    目前提取纹理特征的方法主要采用频谱方法，其建立在时频分析与多尺度分析基础上^[3]，并取得一定的成绩。HALEY G M利用Gabor小波提取纹理特征，但其具有较高的复杂性^[4-5]；MANTHALKAR R^[6]用离散小波包分解方法，但是由于小波不具有方向性信息，因此一定程度上丢失了纹理方向性信息。曲怀敬^[7]采用基于金字塔双树方向滤波器组，结合滤波器的选择和相对相位的统计纹理图像检索，其对系数进行统计建模处理，增加了算法复杂度。由于Curvelet变换相对Gabor变换能够更有效地提取图像曲线特性，近年来在数字图像处理中得到广泛应用^[8]。

    为了图像检索不受纹理旋转变化的影响，提高图像检索性能，本文采用Curvelet变换对纹理图像进行多尺度分析，根据粗尺度反映图像轮廓、细尺度反映图像纹理特性特点，对各尺度系数进行阈值处理，去除噪声等冗余信息，然后采用不同的量化等级，以更好地保留纹理信息。在此基础上计算各尺度系数自相关图，充分考虑量化后不同系数比例和其空间相关性。通过对Brodatz纹理数据库图像检索，证明该方法有效提高图像检索精度。

1 Curvelet变换

    Curvelet变换是一种图像多尺度几何分析工具。第1代Curvelet变换实质是在不同的位置和方向上进行Ridgelet变换，其构造思想是在足够精细的尺度下曲线可近似为直线。为了降低数据冗余度和提高运算速度，第2代Curvelet变换实现过程中并没有用到Ridgelet。离散Curvelet变换中，其频率窗表现为“楔形”且具有任意角度的方向性，所以认为这种频率窗具有“各向异性”的特征。在频域楔形分块中，只有其方向与奇异性特征的几何形状相互匹配情况下，才具有较大的Curvelet特征系数。文献[9]给出了其快速离散实现算法。

    设0≤t₁≤t₂<n，离散Curvelet的系数可定义为：

2 颜色自相关图

    颜色相关图是图像的一种低层特征，其结合了图像中的颜色与空间信息，是图像颜色分布的一种表达方式。这种特征具有旋转不变性，刻画了不同颜色对之间空域相关性，还反映了特定颜色像素在整个图像中的比例。不同于传统的颜色直方图，颜色相关图是用各种颜色之间的量化距离来构建直方图。

    假设I表示一幅N×N图像，图像I中的颜色被量化成m种颜色C₁，…，C_m，对于某个像素点P(x，y)∈I。令I_C={p|I(p)=C}，因此I_Ci表示颜色为C_i的所有像素。图像中2个像素点p₁(x₁，y₁)、p₂(x₂，y₂)之间的距离如下：

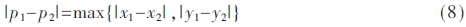
    定义图像I的颜色相关图为：

    γ(i，j，k)表示颜色对为C_i与C_j的像素之间的距离小于等于k的概率。颜色相关图矩阵的大小m²×k，k代表不同距离的总数目。

    如果考虑任意颜色对之间的空间相关性，颜色相关图将会非常复杂和庞大，这样将大大影响处理速度。为了简化处理降低复杂度，引入颜色自相关图。其表示为：

    根据颜色自相关的表达式可以看出其只考虑相同颜色像素对之间的空间关系。自相关图是颜色相关图的子集，其矩阵的大小为m×k，空间需求低于颜色相关图，也更加容易实现。

3 Curvelet相关图算法

    Curvelet充分利用了多尺度分析的特点，因此在时域和频域都具有良好的局部化分析能力，能逐步聚焦到分析对象的任何细节。它引入了尺度、位移和方向3个参量，其不但能反映信号的点奇异性，且具有良好的方向辨识能力。Curvelet相关图充分运用了Curvelet多尺度分析特性和颜色自相关图的旋转不变性，可以用于纹理图像检索。

    算法流程如下：

    （1）对纹理图像进行Curvelet分解；

    （2）各尺度Curvelet系数阈值处理；

    （3）采用不同量化等级量化Curvelet系数；

    （4）计算各尺度系数的自相关图；

    （5）构造特征向量。

3.1 Curvelet图像分解

    对纹理图像进行Curvelet分解需确定其分解层数，层数大小直接影响纹理特征提取的效果和数据量大小。分解层数太小，细尺度下各方向的图像纹理等细节信息不能够被有效提取，数据中包含较多的冗余信息；如果分解层数太大，分解计算时间明显增加，粗尺度下图像的概貌信息会产生一定重合，将丢失一部分图像的基本特征，且影响整体的检索速度。

    Curvelet分解频带划分示意见图1。为了保证既能有效提取图像纹理等细节信息，又加快检索速度，按图1方法确定分解层数。若将纹理图像大小设为N×N，则Curvelet分解尺度变为：

    假设纹理图像大小为128×128，则由式(11)计算得到Curvelet分解层数为3。通过计算可知细尺度高频每层方向数为8的倍数。在本算法中粗尺度为第一层，个数为1，细尺度共有两层，个数分别为16和32，因此总共3层Curvelet分解，将会产生40(=1+16+32)个子带。由于Curvelet分解的方向性，在细尺度层上角度θ和π+θ的分块将具有相同的Curvelet系数，因此在以下的分析中只需要考虑细尺度各层的一半子带，由此得到参与相关图运算的共25(=1+8+16)个子带。

3.2 Curvelet各层系数阈值处理

    在Curvelet频域楔形分块中，只有那些与分块方向相同的奇异特征的几何形状才具有较大的Curvelet特征系数。相对来说，图像中纹理等细节信息Curvelet系数值大于轮廓信息Curvelet系数。因此可以通过阈值处理去掉图像一些冗余信息，阈值处理后各层Curvelet系数为：

    W^M是图像I的第M层Curvelet系数，n_M是与层数相关的参数，σ_M为第 M层Curvelet系数的标准差。

3.3 Curvelet各层系数量化

    由于阈值处理后Curvelet系数仍表现为具有较大分布范围的一组实数，为了便于后面相关图分析，必须对系数进行相应的量化。系数的能量主要分布在粗尺度系数上，此层上包含了图像的轮廓信息。本算法粗尺度的低频系数采用4个量化等级，细尺度的高频系数采用8个量化等级。

3.4 Curvelet自相关图计算

    W^M是图像I的第M层Curvelet系数，对该层进行量化成L级W₁…W_L，且点P₁(x，y)，P₂(x，y)都是属于第M层的Curvelet系数。则Curvelet相关图为：

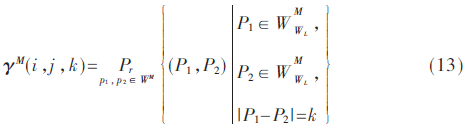
式中k∈{1…K}代表指定距离，i，j∈{1…L}。计算Curvelet自相关图时，选定i=j。由于Curvelet变换的多尺度分析特性，因此总的距离数K的值大小要远小于直接计算颜色自相关图的值大小，本算法中选K=3。

3.5 纹理图像特征向量构造

    Curvelet相关图算法中的特征向量大小与Curvelet分解后各层系数量化大小和自相关图总的距离数相关，其构造简单，总的分量个数为：

由此可得本算法中特征向量的分量个数为60。

4 实验结果

    检索实验图像采用Brodatz纹理库图像，该纹理库包含91幅512×512的灰度纹理图像，共13类图像，且每类图像包含旋转0°、30°、60°、90°、120°、150°和200°后的7幅图像。将91幅图像每幅纹理图像无重叠地分割为16个128×128的图像，将总共得到1 456幅128×128的纹理图像，并将这些图像组成最终的纹理检索测试集。实验将基本的Curvelet检索方法、Md Monirul Islam的基于Curvelet旋转不变特性检索方法和Curvelet相关图方法用于图像数据库中图像检索进行对比，采用精确度(presision)和检索率(recall)进行评价不同算法的检索性能。

    检索返回结果队列中检索到的正确目标图像数与检索结果队列中所有的图像数之比定义为精确度，即：

    检索返回结果队列中检索到的正确目标图像数与数据库中全部的同类目标图像数之比定义为检索率，即：

式中，F为图像库中与检索图像同类的目标图像总数，X代表检索结果队列中的图像总数，Y为查询结果中与检索图像同类的目标图像数。通过对纹理图像库中的每幅图像进行检索，据此得出检索的平均检索精度和查全率，从而给出算法的检索性能评价。

    表1给出了当X=20时，上述3种算法的平均精确度。

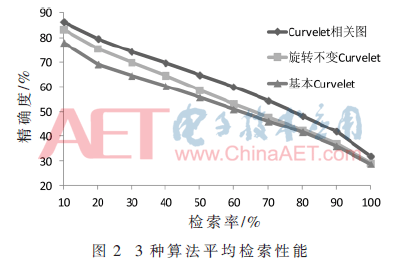
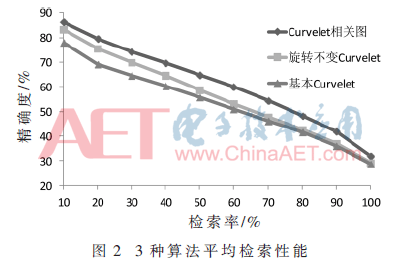
    图2显示3种不同算法的准确度-检索率性能。从图2可以看出，Curvelet相关图检索算法检索性能优于其他两种算法的检索性能，且该方法具有旋转不变性。

5 结论

    本文提出了一种新的基于Curvelet相关图纹理图像检索方法。通过对Brodatz纹理图像库实验，结果表明该方法相较于原有的Curvelet方法能够更有效地进行纹理图像检索。该算法时间复杂度相对于其他方法有所提高。后续研究可以考虑与调整量化等级、颜色距离大小等方法相结合以进一步提高检索效率。

参考文献

[1] SMEULDERS A W M，WORRING M，SANTINI S，et al.Content-based image retrieval at the end of the early years[J].IEEE Trans on Pattern Analysis and Machine Intelligence，2000，22(12)：1349-1380.

[2] 孙君顶，赵珊.图像低层特征提取与检索技术[M].北京：电子工业出版社，2009.

[3] 韩晓晨.图像纹理分割综述[J].科技与企业，2015(9)：76.

[4] HALEY G M，MANJUNATH B S.Rotation-invariant texture classification using a complete space-frequency model[J].IEEE Trans.on Image Processing，1999，8(2)：255-269.

[5] SALEMBIER P，SIKORA T.Introduction to MPEG-7[M].New York：John Wiley & Son Inc.，2002.

[6] MANTHALKAR R，BISWAS P K，CHATTERJI B N.Rotation and scale invariant texture features using discrete wavelet packet transform[J].Pattern Recognition Letter，2003，24(14)：2455-2462.

[7] 曲怀敬，李健，吴延荣，等.结合滤波器选择和相位信息的统计纹理图像检索[J].计算机应用研究，2014，31(12)：3894-3897.

[8] STARCK J L，CANDES E J，DONOHO D L.The curvelet transform for image denoising[J].IEEE Trans.on Image Processing，2002，11(6)：670-684.

[9] CANDES E，DEMANET L，Ying Lexing，et al.Fast discrete curvelet transforms[J].Multiscale Model Simulation，2006，5(3)：861-899.