0 引言

　　多输入多输出(Multiple Input Multiple Output，MIMO)技术可以在不增加带宽和发射功率的前提下，成倍地提高无线通信系统的信道容量，有效解决频谱资源日益紧张和容量需求急剧增长的矛盾[1-2]。因此，对MIMO无线传输技术的研究成为未来移动通信系统的关键所在。在LTE和LTE-A网络中MIMO技术的应用已逐渐趋于成熟，在基站端已经实现了8根天线的信号传输[3]。但是传统MIMO的天线数相对还是太少，而且用户会受到其他用户的干扰，这将急剧降低通信效率。

　　为了有效地利用资源，减少干扰，提高数据的传输速率和鲁棒性，近年来提出了一种在基站端使用大量的天线阵列，被称为大规模MIMO的新技术[4]。目前大规模MIMO技术作为5G移动通信的关键技术之一，受到了业界的广泛关注，逐渐成为国内外研究的热点[5，6]。在大规模MIMO系统中，基站端配备的天线数增加了一个甚至多个数量级，多达100根及以上。随着基站端的天线数大幅增加，信道之间渐近正交[7]。基于这个重要特性，在传统MIMO中性能不理想的简单线性处理方法，比如:匹配滤波(MF)、迫零(ZF)和最小均方误差(MMSE)，都可以应用于大规模MIMO系统中且获得很好的性能。

　　MMSE的估计和检测因为其最小均方误差能获得更准确的判决，相对于MF和ZF，而较广泛地用于无线通信中[8]。但这种检测算法引入了矩阵求逆运算，其计算复杂度随着发射天线数呈立方增长，在大规模MIMO 中难以实时地执行。针对这个问题，文献[9]提出了基于Neumann级数展开的信号检测算法，但是当迭代次数逐渐增大时，计算复杂度减少就不那么明显了。由于大规模MIMO系统MMSE滤波矩阵是对称正定的[10]，本文提出了对称连续超松弛算法，避免了复杂的矩阵求逆，很大程度上降低了计算复杂度。并给出了合适的松弛参数和初始值，用以提高检测性能和收敛速度。此外，基于算法实现的角度考虑，本文还采用了信道硬化信息传递的信道估计方法[11]。

1 大规模MIMO的系统模型

　　本文考虑大规模MIMO系统的上行链路，该系统由一个部署N根天线的基站和K个单天线用户组成。所有用户向基站发送数据时允许使用在相同的时频资源。

　　令sc=[s1，s2，…，sk]T是所有用户同时发送的K×1维符号矩阵，其中sk∈B是来自k个用户的发送符号，B是调制字母表。令Hc∈表示瑞利衰落信道矩阵，则基站端接收到的N×1维信号矢量可以记为：

　　其中，nc表示N×1维均值为0、方差为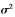的加性高斯白噪声。将复数模型式(1)转化为等价的实数模型，并省略下标可以得到：

　　其中，s∈R2K，H∈R2N×2K，y∈R2N，n∈R2N，即有：

　　其中，R(·)和J(·)分别代表实部和虚部。

　　通过MMSE检测发送的信号矢量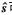可以表示为：

　　其中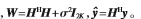

　　随着基站天线数与用户数的比值越来越大，MMSE检测可以接近最优的检测性能，但同时加权矩阵求逆W-1的计算复杂度随着用户数呈立方增长，增加了硬件的实现难度。

2 对称连续超松弛检测算法

　　2.1 基于SSOR信号检测

　　观察式(7)可知，矩阵求逆W-1的计算复杂度为O(K3)。对大规模MIMO系统而言，K值通常很大，比如K=32，这使得MMSE检测器的计算复杂度很庞大。但是大规模MIMO系统，信道矩阵H的列之间渐进正交[7]，矩阵W具有对称正定性[10]。基于这个重要特性，可以利用SSOR以很低的复杂度获得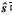。不同于MMSE信号检测直接计算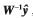，SSOR通过迭代避免矩阵求逆的计算，具体操作分为以下3个步骤：

　　(1)分解Hermitian正定矩阵W，记为：

　　其中，D、L和LH分别表示W的对角元素矩阵、严格的下三角和严格的上三角元素矩阵。

　　(2)计算前半部分迭代，和连续超松弛迭代(SOR)[12]一样。

　　(3)计算后半部分迭代，和连续超松弛迭代(SOR)逆序一样。

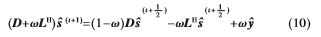
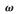　　其中，t=0，1，…指迭代次数，(0)指初始解，通常情况下都取零向量[12]。指松弛参数，0<<2，影响收敛和收敛速度。SSOR可以被视为SOR的改进版。相较于SOR，SSOR有两个优势：①SSOR迭代是对称的，能利用切比雪夫加速法[12]加快算法的收敛速度；②SSOR迭代的收敛速度对松弛参数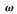不是很敏感，这意味着可以选取简单且经过量化后的松弛参数。

　　2.2 量化松弛参数和初值

　　由式(9)和式(10)可以看出，松弛参数?棕的选取影响着基于SSOR检测算法的收敛速度。文献[12]得出最佳松弛参数为：

　　其中，?籽(BJ)是Jacobi迭代矩阵BJ的谱半径，可以表示为：

　　大规模MIMO系统，对角矩阵D的元素会收敛于一个定值N，则有：

　　并且，当N和K的值足够大且K/N接近定值时，矩阵W的最大奇异值可以近似为：

　　通过上述的分析，提出了一个简单的接近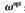的量化松弛参数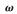，记为：

　　由式(15)和式(16)可知，量化后的松弛参数仅由系统结构参数N和K决定。一旦大规模MIMO的结构固定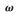，则为一个定值，所以基于SSOR检测算法的收敛率对松弛参数不是很敏感。

　　为了方便实现，传统迭代算法通常设置初始值为零向量。但是选择一个合适的初始值，可以加快收敛速度，并能获得更好的检测性能。当基站端配备的天线数远大于用户数(N>>K)时，W近似于对角矩阵D，且HHH≈NI2K。根据信道硬化现象，可得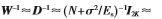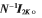N-。则有，式(9)式(10)的初始解向量可以选为：

　　2.3 复杂度分析

　　本小节将在算法所需的乘法器的个数上对基于SSOR检测算法进行计算复杂度的分析。根据2.1节可知，SSOR每次迭代的计算复杂度分为两部分。

　　(1)第一部分计算复杂度来自于式(9)，其解可以表示为：

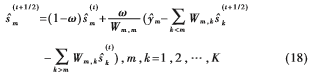
　　其中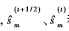，和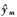分别代表式(9)中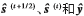的第m个元素，Wm，k代表W第m行第k列。很明显，计算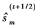需要K+1次乘法，因为)中有K个元素，则这部分所需要乘法器的个数为K2+K。

　　(2)第二部分计算复杂度来自于式(10)的计算，类似于式(18)、式(10)的解可以表示为：

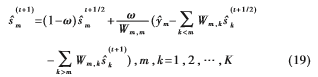
　　其中，表示式(10)中的第m个元素，根据式(19)，可以得到这部分也需要K2+K次乘法运算。

　　综上所述，基于SSOR的检测算法总的计算复杂度为t(2K2+2K)。图1对比了基于Neumann级数展开信号检测算法、基于SSOR信号检测算法以及MMSE检测算法计算复杂度。结果表明，当迭代次数t≥3时，基于Neumann级数展开信号检测器的计算复杂度为O(K3)。相比之下，对于任意的迭代次数，基于SSOR信号检测器的计算复杂度都是O(K2)。

　　2.4 基于CHEMP的信道估计

　　由于准确的信道状态信息(Channel State Information, CSI)对上行链路的信号检测有着决定性作用，因而获得精确的信道估计对于大规模MIMO系统来说至关重要。根据所提出基于SSOR信号检测算法的特点，可以利用CHEMP接收机[11]直接对格拉姆矩阵G=HHH进行估计，而不是估计信道矩阵H。

　　假设信道是慢衰落，Xp=Ppilot I2K表示发送的导频矩阵，发送导频的功率为，则基站端接收到的导频矩阵为Yp=HXp+Vp=Ppilot H+Vp，其中Vp表示噪声矩阵。

　　格拉姆矩阵G的估计为：

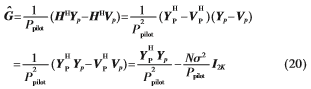
　　匹配滤波器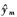的估计可以通过以下公式计算得到：

3 仿真结果

　　为了验证基于SSOR信号检测算法的性能，本节对比分析了基于SSOR信号检测算法、基于Neumann级数展开信号检测算法以及MMSE信号检测算法的误比特率(Bit Error Rate，BER)。设置仿真时的传输信道为准静态瑞利衰落信道，基带信号调制方式为16-QAM调制，天线规模N×K为128×16。仿真结果见图1～图3，图中，t表示SSOR迭代的次数以及Neumann级数的展开项数。

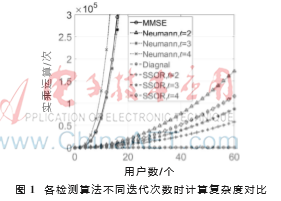
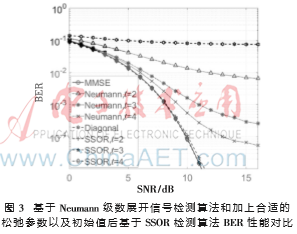
　　图2显示了在大规模MIMO天线结构N×K为128×16，未加合适的松弛参数和初始值时，基于Neumann级数展开信号检测算法和基于SSOR信号检测算法BER性能的比较。由图2可以看出，随着Neumann级数和SSOR迭代次数不断的增加，信号检测性能也在提高。但是相同次数的迭代，基于SSOR信号检测性能比基于Neumann级数信号检测性能好很多。比如：在迭代次数t=4，达到10-4的BER性能时，基于Neumann级数展开信号检测所需的信噪比为14 dB，而基于SSOR信号检测算法仅需约10 dB。同时，基于SSOR信号检测算法通过少数的迭代，能达到接近MMSE算法的检测性能。比如：迭代次数t=3时，本文所提的算法能达到接近MMSE最优的检测性能。

　　图3显示，在大规模MIMO天线结构N×K为128×16时，加上合适的量化松弛参数和初始值后，基于SSOR检测有更优的检测性能，在迭代次数为t=2，达到10-4的BER性能，未加合适的量化松弛参数和初始值时，所需信噪比为16 dB，而加上合适的松弛参数和初始值后，所需信噪比仅为10 dB，且曲线收敛更快。在迭代次数t=2时，就能达到接近MMSE最优的检测性能。仿真结果显示，本文所提出的算法在几次迭代后，便能达到接近最佳的信号检测性能。

4 总结

　　本文提出了基于SSOR低复杂度信号检测算法，利用大规模MIMO系统的特性和松弛迭代方法，避免了复杂的矩阵求逆，大量降低了计算复杂度。并给出了合适的松弛参数和初始值，加快了收敛速度。此外，当考虑到信道估计时，还提出了一种有效的信道估计算法，进一步降低了计算的复杂度。

　　参考文献

　　[1] LARSSON E.Very large MIMO system：opportunity and challenges[J].IEEE Trans Wireless Commum.，2010,9(11)：2590-3600.

　　[2] LU L，LI G Y，SWINDLEHURST A L，et al.An overview of massive MIMO：Benefits and challenges[J].IEEE Journal of Selected Topics in Signal Processing，2014，8(5)：742-758.

　　[3] LARSSON E，EDFORS O.Massive MIMO for next generation wireless systems[J].IEEE Communications Magazine，2013，52(2)：186-195.

　　[4] RUSEK F，PERSSON D，LAU B K，et al.Scaling up MIMO：Opportunities and challenges with very large arrays[J].IEEESignal Processing Magazine，2012，30(1)：40-60.

　　[5] BOCCARDI F，HEATH R W，LOZANO A，et al.Five disruptive technology directions for 5G[J].Communications Magazine IEEE，2014，52(2)：74-80.

　　[6] QIAN M，WANG Y，ZHOU Y，et al.A super base station based centralized network architecture for 5G mobile communication systems[J].Digital Communications & Networks，2015，54(2)：152-159.

　　[7] MARZETTA T L.Noncooperative cellular wireless with unlimited numbers of base station antennas[J].IEEE Transactions on Wireless Communications，2010，9(11)：3590-3600.

　　[8] HONIG M，MADHOW U，VERDU S.Blind adaptive multiuser detection[J].Information Theory IEEE Transactions on，2010，6(4)：5pp.-3737.

　　[9] WU M，YIN B，WANG G，et al.Large-scale MIMO detection for 3GPP LTE：Algorithms and FPGA implementations[J].Selected Topics in Signal Processing IEEE Journal of，2014，8(5)：916-929

　　[10] GAO X，DAI L，YUEN C，et al.Low-complexity MMSE signal detection based on Richardson method for largescale MIMO Systems[C].Vehicular Technology Conference (VTC Fall)，2014 IEEE 80th.IEEE，2014：1-5.

　　[11] NARASIMHAN T L，CHOCKALINGAM A.Channel hardening-exploiting message passing(CHEMP) receiver in large-scale MIMO systems[J].Selected Topics in Signal Processing IEEE Journal of，2013，8(5)：847-860.

　　[12] BJ?魻RK A.Numerical methods in matrix computations[Z].Texts in Applied Mathematics，2015.