文献标识码: A
DOI:10.16157/j.issn.0258-7998.2016.09.028
中文引用格式: 孔范增,任修坤,郑娜娥. 基于GDOP权值交点的鲁棒AOA定位算法[J].电子技术应用,2016,42(9):107-110.
英文引用格式: Kong Fanzeng,Ren Xiukun,Zheng Nae. A robust AOA positioning algorithm based on GDOP-weighted intersection[J].Application of Electronic Technique,2016,42(9):107-110.
0 引言
近年来无线传感器网络(Wireless Sensor Network,WSN)在很多领域得到了广泛的应用,如目标的定位与跟踪和动物行为监控等。而精确的目标位置信息是上述应用的基础,因此,无线传感器网络的定位技术一直是研究的热点。基于距离的定位算法可利用到达时间(TOA)、到达时间差(TDOA)和到达角度(Angle of Arrive,AOA)等测量值,实现对目标的定位。其中,AOA的测量精度高于TOA和TDOA,基于AOA的定位算法不需要各传感器之间进行时钟同步[1,2],但是AOA测量设备的尺寸和成本限制了它的应用,然而信号处理技术和设备制造技术的发展很好地解决了上述问题,所以近年来基于AOA的定位算法又得到了关注。
关于基于AOA的定位算法,相关学者已经做了很多研究。文献[1-3]利用锚节点与目标的方位线两两之间的交点进行加权求和估计目标的位置,这类算法可称为基于权值交点的AOA定位算法。文献[3]提出了CAOA算法,该算法将所有的方位线交点的均值作为目标的估计位置。文献[4,5]提出了SA算法,利用方位线交点的闭式解的一阶或二阶偏导定义各交点的敏感度,生成相应的权值,再进行加权求和。文献[1,2]在定位误差分析的基础上提出了基于权值方位线交点的定位算法。文献[1]提出WIAOA算法利用锚节点之间的距离、锚节点与目标的AOA测量值及其标准差构建方位线交点的权值。文献[2]提出的CWIAOA定位算法利用方位线交点的CRLB值得到交点的权值。而某些交点虽具有较大的权值,但其与目标真实位置之间的偏差却比权值较小的交点的偏差大,将这样的交点用于目标位置的估计会严重影响估计的精度,这样的交点可称为奇异方位线交点。
本文给出了一种基于GDOP(Geometric Dilution of Precision)权值交点的鲁棒AOA定位(RGWIAOA)算法,该算法利用圆误差概率剔除奇异方位线交点,将剩余的方位线交点视为有效交点,对有效交点赋予相应的归一化权值并进行加权求和,完成对目标的位置估计。算法只对有效交点进行加权求和,同时在权值的计算中考虑了锚节点的位置误差,使算法有较高的定位精度,并且在不同的应用环境下具有较好的鲁棒性。
1 模型的建立
AOA算法利用锚节点测量盲节点信号的达到角度,建立锚节点与盲节点之间的方位线,两条方位线的交点即为盲节点位置的粗估计值。这里假设各锚节点与盲节点之间不存在遮挡,即信号传播存在直达径,锚节点能测量定位信号的AOA。
假设有N个位置已知但存在误差的固定锚节点, 和
和 分别表示第i个锚节点的已知位置和真实位置,nxi为xi与
分别表示第i个锚节点的已知位置和真实位置,nxi为xi与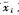 之间的误差,nyi为yi与
之间的误差,nyi为yi与 之间的误差,nxi和nyi均服从零均值的正态分布,标准差分别为?滓xi和?滓yi,
之间的误差,nxi和nyi均服从零均值的正态分布,标准差分别为?滓xi和?滓yi, 。
。 表示第i个锚节点AOA的测量值,
表示第i个锚节点AOA的测量值, 表示第i个锚节点AOA的真实值,ni表示第i个锚节点AOA测量值的误差,其服从均值为零且标准差为?滓i的正态分布。盲节点的位置是未知的,用p=(xT,yT)表示其真实位置。算法对盲节点位置的估计结果用
表示第i个锚节点AOA的真实值,ni表示第i个锚节点AOA测量值的误差,其服从均值为零且标准差为?滓i的正态分布。盲节点的位置是未知的,用p=(xT,yT)表示其真实位置。算法对盲节点位置的估计结果用 表示。定位模型可以用如下公式表示:
表示。定位模型可以用如下公式表示:



其中,

2 基于GDOP权值交点的鲁棒AOA定位算法
基于权值交点的AOA定位算法的核心思想是,在获得所有连接锚节点和盲节点的方位线间的两两交点的基础上,对交点进行加权求和,作为目标位置的估计值,其一般公式为:

式中,N为锚节点的个数, 和
和 分别为方位线交点
分别为方位线交点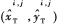 在x轴和y轴上的归一化权值,不同算法的区别在于
在x轴和y轴上的归一化权值,不同算法的区别在于 和
和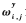 的确定过程。
的确定过程。
为提高基于权值交点的AOA定位算法的定位精度,首先应剔除那些权值较高但偏离盲节点实际位置距离较大的方位线交点。为此可以考虑引入圆误差概率解决这个问题。二维环境下圆概率误差的定义为定位结果落到以锚节点真实位置为中心的圆形区域C的概率。圆形区域C这里称为误差概率圆,它的半径定义为几何精度因子半径的n倍[6],由式(5)确定,其中RCEP-P表示定位结果以概率P落入圆形区域C的半径。根据文献[6],式(5)中P与n的关系可由式(6)确定,通过推导得到式(7)。



圆形区域C的圆心为盲节点的真实位置,而对于定位问题,盲节点的位置是未知的。这里以方位线的交点 代替盲节点的真实位置(xT,yT),其误差概率圆的半径可由下式得到:
代替盲节点的真实位置(xT,yT),其误差概率圆的半径可由下式得到:

其中, 代表方位线i和方位线j的交点的误差概率圆的半径。N条方位线共有
代表方位线i和方位线j的交点的误差概率圆的半径。N条方位线共有 个交点,若方位线交点
个交点,若方位线交点 与
与 之间的距离
之间的距离 满足:
满足:

则认为 和
和 为有效交点。在概率为P条件下,找出有效交点,将有效交点用于盲节点的位置估计,从而减小奇异方位线交点对定位精度的影响。
为有效交点。在概率为P条件下,找出有效交点,将有效交点用于盲节点的位置估计,从而减小奇异方位线交点对定位精度的影响。
下面讨论GDOP的计算问题。在考虑锚节点的位置存在误差的情况下,根据式(3)对 求微分,得:
求微分,得:

其中:



令
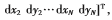 ,且:
,且:


得:

利用伪逆求解盲节点定位误差估计值为:

假设各锚节点的AOA测量误差互不相关,且锚节点位置误差各元素之间及各锚节点位置误差也互不相关,故:
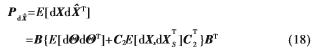
式中,
上述GDOP的计算方法,既考虑了锚节点的AOA测量误差,也考虑了锚节点位置的误差,具有较强的适应性。这里仍然以方位线i和方位线j的交点代替盲节点的真实位置,得到:

综上,方位线i和j的交点 ,在x轴和y轴上的非归一化的权值为:
,在x轴和y轴上的非归一化的权值为:

式中, 和
和 分别代表矩阵
分别代表矩阵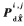 的主对角线上的两个元素。所有有效方位线交点构成的集合为
的主对角线上的两个元素。所有有效方位线交点构成的集合为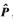 ,令:
,令:

若方位线交点 不属于
不属于 ,则:
,则:

若方位线交点 属于
属于 ,则其归一化权值表示为:
,则其归一化权值表示为:

根据式(22)、式(23),对各方位线交点进行加权求和,盲节点位置的估计值为:

综上所述,本文所给的基于GDOP权值交点的鲁棒AOA定位算法主要包括以下三步:(1)锚节点获得AOA测量值;(2)得到方位线交点,确定有效交点;(3)有效交点加权求和,估计目标位置。RGWIAOA算法的具体步骤如下:
初始化:锚节点(xi,yi)或 ,i=1,2,…,N,AOA测量值
,i=1,2,…,N,AOA测量值 ,圆误差概率P=0.5,有效交点个数门限
,圆误差概率P=0.5,有效交点个数门限 。
。
算法过程:盲节点(xT,yT)定位。
(1)获得方位线交点 ;
;
(2)分别根据式(19)计算GDOPi,j;
(3)分别根据式(8)计算 ;
;
(4)计算方位线交点 之间的距离,根据式(23)确定有效交点集合
之间的距离,根据式(23)确定有效交点集合 ;
;
(5)若有效交点个数小于 ,则加大圆误差概率P并重复步骤(3);
,则加大圆误差概率P并重复步骤(3);
(6)根据式(20~23)计算各方位线交点的权值;
(7)根据式(24)估计盲节点的位置。
3 仿真结果与分析
为验证本文所给算法的性能,本节在几种典型场景下对RGWIAOA算法、CAOA算法、WIAOA算法、CWIAOA算法和SA算法的定位性能进行比较。在每个场景下,每种算法进行1 000次Monte-Carlo仿真,统计算法的均方根误差。
(1)场景1:6个锚节点沿半径为60 m的圆形边缘均匀分布,锚节点位置分别为(120,0)、(90,51.96)、(30,
51.96)、(0,0)、(30,-51.96)和(90,-51.96),且锚节点的已知位置与真实位置相比不存在误差,盲节点位置为(60,0)。各锚节点对盲节点的AOA测量值的误差互不相关,且 的取值范围为[1°,5°]。
的取值范围为[1°,5°]。
图1为场景1下各算法的RMSE随?滓?兹变化的曲线。从图 1中可以看出在场景1下,CAOA算法的性能最差,其RMSE偏离CRLB较远,其他算法性能接近,且它们的RMSE基本达到CRLB。

(2)场景2: 6个锚节点沿直线等间距分布,间距为20 m,锚节点位置分别为(-50,0)、(-30,0)、(-10,0)、(10,0)、(30,0)和(50,0),且锚节点的已知位置与真实位置相比不存在误差,盲节点位置为(0,60)。各锚节点AOA测量值的误差互不相关,且 取值范围为[1°,5°]。
取值范围为[1°,5°]。
图2为场景2下各算法的RMSE随 变化的曲线。从图 2中可以看出在场景2下,CAOA算法的性能最差,其RMSE偏离CRLB的程度随
变化的曲线。从图 2中可以看出在场景2下,CAOA算法的性能最差,其RMSE偏离CRLB的程度随 的增加而增大,RGWIAOA算法的整体性能优于其他算法,但当
的增加而增大,RGWIAOA算法的整体性能优于其他算法,但当 >4°时RGWIAOA算法的RMSE与CRLB有较小的偏离。
>4°时RGWIAOA算法的RMSE与CRLB有较小的偏离。

对比场景1和场景2,可以发现上述几种算法的定位性能在场景1下比在场景2下要好,即锚节点分布盲节点的周围时,算法的定位性能比较好。
(3)场景3:锚节点位置误差各元素之间及各锚节点位置误差也互不相关,且 其他条件与场景2一致。
其他条件与场景2一致。
图3为场景3下各算法的RMSE随?滓?兹变化的曲线。从图 3中可以看出在场景3下,CAOA算法的性能最差,其RMSE偏离CRLB的程度随?滓?兹的增加而增大,RGWIAOA算法的整体性能优于其他算法。但由于锚节点的已知位置存在误差,将其用于位置解算,故上述5种算法的RMSE与CRLB相比均会存在一定的偏差。对比图 3和图 2还可以发现,在 一定的情况下,
一定的情况下, 对算法性能的影响会随着
对算法性能的影响会随着 增大而相对减弱。
增大而相对减弱。

综上所述,仿真结果表明,本文所给RGWIAOA算法在不同场景下,较其他几种算法有更好的适应性,且该算法的定位精度在整体上优于其他算法。
4 结束语
本文给出了一种基于GDOP权值交点的鲁棒AOA定位算法。算法的核心思想是在所有方位线交点的基础上利用圆误差概率确定有效交点,根据有效交点的GDOP为其赋予相应的权值,并对有效交点进行加权求和,得到目标的位置估计。RGWIAOA算法充分利用了锚节点AOA测量值的标准差,同时在GDOP的计算中考虑了锚节点自身位置的误差对计算结果的影响。仿真结果表明,RGWIAOA算法与WIAOA算法、CWIAOA算法、SA算法和CAOA算法相比,具有更好的适应性,且算法的整体定位精度更高。
参考文献
[1] ZHOU Q,DUAN Z.Weighted intersections of bearing lines for AOA based localization[C].Information Fusion (FUSION2014),2014 17th International Conference on.University of Salamance:IEEE,2014:1-8.
[2] DUAN Z,ZHOU Q.CRLB-weighted intersection method for target localization using AOA measurements[C].Computational Intelligence and Virtual Environments for Measurement Systems and Applications(CIVEMSA),2015 IEEE International Conference on,Shenzhen China:IEEE,2015:141-146.
[3] BRIDA P,MACHAJ J,BENIKOVSKY J,et al.A new complex angle of arrival location method for ad hoc networks[C].Proceedings of the 7th Workshop on Positioning Navigation and Communication(WPNC 07),Dresden Germany:IEEE,2010:284-290.
[4] SOLTANIAN M,PEZESHK A M,MAHDAYI A,et al.A new iterative position finding algorithm based on taylor series expansion[C].Electrical Engineering(ICEE),2011 19th Iranian Conference on,IEEE,2011:1-4.
[5] PEZESHK A A M,DALLAI M.A novel method for position finding of stationary targets using bearing measurements[C].Proceedings of the C4I Conference at Sharif University of Technology,2010.
[6] YU K G,SHARP I,GUO J Y.Ground-based wireless positioning[M].Chichester:Wiley-IEEE Press,2009.

