0 引言

　　人脸识别一直是近年来计算机视觉领域中的重要研究方向，被用于门禁、生物入侵、安防等实际应用环境中。然而，人脸识别仍然是一个具有挑战的问题，例如遮挡、伪装、光照变化等噪声对人脸图片的影响会导致后续识别效果下降。从几十年前至今，众多学者在人脸识别技术的发展中对这些问题进行了研究，提出了许多针对这些问题的富有建设性的算法。

　　原始的局部二值模式（Local Binary Patterns，LBP）算法是由OJALA T等人提出的用于纹理分类的方法[1]，它是一个由局部像素比较获得的二进制序列。AHONEN T等人将LBP用于人脸识别领域并将其改进为对光照变化具有鲁棒性的方法[2]。在文献[3]中，LBP通常用来处理人脸识别中的光照问题。实验表明，经过LBP处理后的图片比原始图片在识别时具有更强的鲁棒性。近年来，Liu Guangcan等人提出了低秩表示的算法[4]（Low-Rank Representation，LRR），该算法可以对子空间进行分类。LRR的目的是寻找一个字典中所有向量表示一个基于候选线性组合的最低秩表示。基于局部特征对处理人脸图片时的鲁棒性和低秩表示分类的框架，结合近年来被广泛用于克服提取特征和分类时线性方法的极限的核方法，本文提出了一种基于局部特征与核低秩表示的人脸识别算法。

1 相关知识

　　1.1 低秩表示

　　Liu Guangcan等人[4]提出了对子空间结构进行分析的低秩表示算法(LRR)，该方法也可以用于对线性子空间的数据进行无监督分类。如果给定一个适当的字典，LRR可以学习到所有观测向量通过字典原子的所有可能线性组合表示中的最低秩表示[5]。秩最小化的问题可以通过下式求解：

　　其中X是一个测试数据矩阵，X的每一列是都一个测试对象。A是一个字典，Z是字典A对X的一个低秩表示。式(1)中求秩最小的问题可以通过求核范数来代替，则式(1)可改写为：

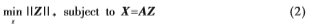
　　当数据有噪声干扰时，LRR的优化模型定义如下：

　　其中A·Z是低秩部分，E是与X相关的误差(或噪声)部分，||E||2，1是适应于不同遮挡模型的误差项，适用于小的高斯噪声，||E||1适用于随机遮挡，>0是低秩和误差两部分的平衡因子。已经有许多学者提出了低秩恢复问题的解法，例如迭代阈值法[6]、加速近端梯度法[7]、增广拉格朗日法[8](Augmented Lagrange Multiplier，ALM)。其中ALM方法有着更快的速度和更高的准确度，本文采用ALM方法来处理低秩问题。

　　1.2 核函数

　　核函数是一项众所周知的应用于机器学习中的技术，如SVM、KPCA、KFDA算法[9]中都应用了核函数。通过核函数可以将原始的特征空间通过非线性映射转换到一个高维的核特征空间，并且在高维空间将问题转换为线性问题解决[10]。例如多项式核k(x，y)=(〈x+y〉+c)d和高斯核k(x，y)=exp(-γ||x-y||2)都是常见的核函数，其中d和γ是核函数的参数。

2 基于局部特征与核低秩表示的人脸识别算法（LKLRR）

　　2.1 局部特征提取

　　LBP是用于描述局部纹理算子，通过比较围绕像素的计算值的特征表征的二进制序列，然后将该序列转化为十进制数来表示该点的特征[1]。过多的二进制模式会给计算带来不便，OJALA T采用了一种新的“等价模式”来解决这一问题，同时该算法也提高了LBP的统计特性并对LBP算子的模式种类进行降维。OJALA T的“等价模式”表示如下：当从0→1或从1→0相应的循环LBP二进制数跳两次时，对应二进制模式LBP被称为等价类模式，另一种类型便为混合模式。改进后的二进制模式类型降低的同时也不会使任何信息丢失。这使得特征向量的维数更少，并能消弱高频噪声的滋扰。

　　2.2 基于局部特征与核低秩表示

　　假设一个经过LBP特征提取后的样本通过一个非线性映射从原始的特征空间Rm映射到高维特征空间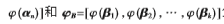分别表示由所有训练样本和测试样本所组成的矩阵通过非线性映射?渍转换到高维特征空间，其中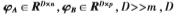就是上述高维空间F。通过式（4）可以将测试样本图片在核特征空间F中通过训练样本图片线性表示。

　　因此，在核空间中的低秩表示问题可以通过式（5）来表示：

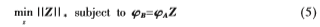
　　其中Z为训练样本矩阵在高维核特征空间对测试样本矩阵最低秩表示。其中和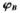都未知，从而式（5）无法直接求解。将样本特征空间F中进行降维处理，也就是样本图片从F空间映射到其低维子空间中，假设P∈RD×d是F中的变换矩阵，求解式（5）可通过式（6）来实现：

　　其中映射矩阵P是与图片相关的矩阵，通过应用KPCA中的核降维方法，映射矩阵中的向量是空间F中与图片线性相关的向量，表示如下式：

　　其中Pj为P∈[P1，P1，…，Pd]=RD×d中的第j个向量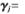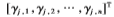，是与第j个变换向量相关的伪变换向量。令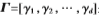是伪变换矩阵，则变换矩阵P可以通过下式表示：

　　将式(8)带入式(6)，则有：

　　其中核矩阵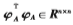和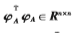由相应的核函数计算得出。对于样本α和β，则有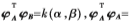其中k(:，:)表示一个核函数。令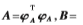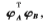，则式（1）的约束表达式可以通过式（5）来代替，则优化问题转为下式：

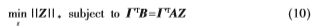
　　考虑到噪声对样本的影响，将式（10）转化为如下更加鲁棒的优化模型：

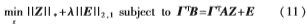
　　其中E表示高维空间中的相关误差。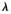＞0表示两部分的平衡因子。其中转换矩阵通过应用KPCA中降维获得变换矩阵的方法计算得出，伪变换向量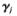j可以通过求解特征值的方法计算：

　　将归一化后的特征向量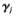进行排序，选择最大的前d个特征值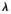j，j=1，2，3，…d所对应的特征向量则可获得伪转换矩阵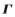祝。将其代入优化后的模型，则可通过求解低秩表示的问题来进行后续的分类判别。

　　具体的算法步骤如下：

　　（1）输入：i类训练样本矩阵A∈Rm×n，k个测试样本矩阵B∈Rm×k；

　　（2）分别对训练样本和测试样本进行LBP特征提取后进行核变换得到训练样本的LBP核矩阵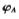和测试样本的LBP核矩阵；

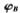　　（3）将样本通过映射函数进行处理，随后获得高维特征空间中的训练和测试样本的特征矩阵；

　　（4）通过特征值和特征向量的方法求解伪变换矩阵后对高维特征矩阵进行降维；

　　（5）对降维后的测试和训练特征矩阵通过式（11）进行低秩表示获得系数矩阵Z；

　　（6）通过下式计算每个样本与每类样本之间的残差：

　　其中l=1，2，…，k；j=1，2，…，i。

　　（7）输出：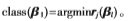

3 实验结果及分析

　　本部分将本文提出的LKLRR与SRC、CRC和LRR等算法分别在AR、Extended YaleB、FERET等人脸库进行了光照、表情及遮挡变化实验对比。实验表明，本文提出的基于局部特征与核低秩表示的人脸识别算法的识别率比其他几种方法的识别率要高，而针对有遮挡和伪装的人脸图片提出的基于局部特征与核低秩表示的人脸识别算法的识别率也有更强的鲁棒性和识别率。

　　3.1 Extended Yale B数据库光照变化

　　Extended Yale B人脸库由38个人的2 414幅正面人脸组成，其中每人大约有64幅图像，来自64种实验光照条件。图1为该人脸库中部分人脸图片。本部分实验随机地选择每人32幅图片作为训练样本集，其余的32幅人脸图片作为测试样本集。每幅图片都调整为96×84。表1给出了不同方法在该人脸库中的识别率。

由表1可以看出，图片进行LBP特征提取后，通过低秩表示进行分类的方法对于人脸图片的识别率增加，增加了核函数的低秩表示，表现出更加优越的识别性能。

　　3.2 AR数据库光照及表情变化

　　在AR人脸数据库中选择50名男性和50名女性构成一个人脸数据库，提取每人14幅人脸图片，包括人脸图像的表情和光照变化，其中7幅作为训练样本，其余的作为测试集。图像尺寸统一调整为83×60。表2显示多种算法在该人脸库上的比较。由表2可看出，本文的算法相比其他算法识别率明显提高。

　　3.3 FERET数据库姿态偏转

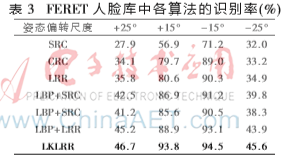
　　FERET数据库中包含了200个人，每人7幅总共1 400幅表情、光照以及不同尺度下的姿态变化人脸图片。图2为实验中某个目标的图像，从左到右分别为标准、表情变化、光照变化、偏转-25°、偏转-15°、偏转+15°、偏转+25°的人脸图像。采用前3幅人脸图片作为训练集，其余4个偏转角度不同的图片分别作为4个测试集。所有的图片均裁剪为80×80。表3为FERET数据库中姿态偏转尺度不同的情况下多种算法的识别率比较。表3可以明显反映出提出的LKLRR算法相较于其他集中算法识别率有着显著的优势，尤其是在测试集姿态偏转尺度较大时（+25°和-25°）明显提高。

　　3.4 伪装实验

　　本部分采用了AR人脸库进行实验，其中每人选取7幅人脸图片进行训练，3幅墨镜遮挡、3幅围巾遮挡的人脸图片进行测试，同样将每幅图片的大小调整为83×60，表4是各个方法分别对于墨镜遮挡和围巾遮挡的人脸识别率比较，从表中可以看出本文的方法对于伪装的人脸图像的识别率较其他方法有很大的提高。

4 总结

　　针对人脸图片的遮挡、伪装、光照及表情变化等问题，本文提出基于局部特征与核低秩表示的人脸识别算法。首先将样本通过描述局部特征的LBP算子进行特征提取，加强了图像的局部细节特征。随后将特征转换到高维的特征空间后进行核低秩表示来进行后续的分类识别。实验表明，本文的LKLRR算法在处理遮挡、伪装以及光照变化等问题时的鲁棒性更强，识别率更高。

　　参考文献

　　[1] OJALA T，HARWOOD I.A comparative study of texture measures with classification based on feature distributions[J].Pattern Recognition，1996，29(1)：51-59.

　　[2] AHONEN T，HADID A，PIETIK?魧INEN M.Face recognition with local binary patterns[C].Lecture Notes in Computer Science，2004，3021：469-481.　

　　[3] Yuan Xiaotong，Liu Xiaobai，Yan Shuicheng.Visual classification with multitask joint sparse representation[J].IEEETransactions on Image Processing A Publication of the IEEE Signal Processing Society，2010，21(10)：3493-3500.

　　[4] Liu Guangcan，Lin Zhouchen，Yan Shuicheng，et al.Robustrecovery of subspace structures by low-rank representation[J].IEEE Transactions on Software Engineering，2012，35(1)：171-184.

　　[5] ZHANG Y，JIANG Z，DAVIS L S.Learning Structured lowrank representations for image classification[C].Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition.IEEE Computer Society，2013：676-683.

　　[6] DAUBECHIES I，DEFRISE M，MOL C D.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J].Communications on Pure & Applied Mathematics，2003，57(11)：1413-1457.

　　[7] BECK A，TEBOULLE M.A fast iterative shrinkage-thresh-olding algorithm for linear inverse problems[J].Siam Journal on Imaging Sciences，2009，2(1)：183-202.

　　[8] BERTSEKAS D P.Constrained optimization and Lagrangemultiplier methods[M].Athena Scientific，1996.

　　[9]  SMOLA A，M?譈LLER K.Nonlinear component analysis as a kernel eigenvalue problem[C].Neu.Img.2006：1299-1319.

　　[10] KANG C，LIAO S，XIANG S，et al.Kernel sparse representation with local patterns for face recognition[C].ImageProcessing(ICIP)，2011 18th IEEE International Conferenceon.IEEE，2011：3009-3012.