0 引言

    异构网是应对日益增长的数据传输需求挑战的一种有效途径。文献[1]提出了一种新型的无线云接入网络，并在文献[2]中给出了详细的描述。之前针对异构网资源管理的研究主要分为两个场景：单接入网的资源分配和多接入网的资源分配。在第一个研究场景中，移动终端只能从单一的接入网中获取资源^[1-3]。在第二个场景中，移动终端可以同时从所有可用的无线接入网络中获取资源，因此也被称为多寻解方案^[4]。之前的研究都集中在提高传统的多队列网络的延迟性能。一种方法是使用大偏差理论将平均延迟约束转化为等效平均速率，再利用约束条件下的信息理论公式求解优化问题^[5]；另一种方法是使用李雅普诺夫稳定性理论来建立一个高吞吐量的最优控制方案，例如计算机资源优化^[6]，或实现分组交换系统的稳定^[7-9]。

    本文的研究主要集中在基站用户需求队列的稳定性，采用李雅普诺夫漂移保证队列的稳定性和改进的匈牙利来实现更高效的资源分配。

1 系统模型与问题分析

1.1 网络模型

    如图1所示，本文提出了一种多队列多服务的异构云无线接入网络架构。在该架构中，将节点视为队列并将节点中等待服务的用户视为队列成员，根据节点的流量来调节不同节点用户的相互转移。

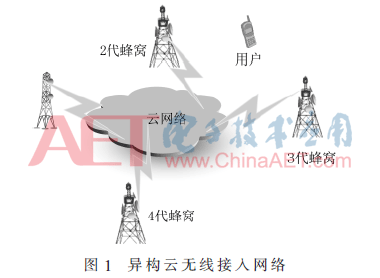
    假设异构云无线接入网络有n(n∈{1，2，…，N})个节点，节点间有l(l∈{1，2，…，L})传输链路。图2给出了多用户多服务系统图，其中λ_n表示网络外新到达第n个节点的数据，a_n表示第n个节点包括新到达数据和节点间转移数据在内的总的数据，从节点a到节点b的数据转移表示为((a_l，b_l)，a，b∈{1，2，…，N})。S(t)∈S表示网络的拓扑状态，S是状态集。在平稳状态下，S(t)被认为是恒定的。I(t)∈I_S表示分配控制决策，I_S表示在给定状态S下的所有资源分配决策集。该网络结构的特点是：S(t)是根据一个有限状态空间S和时间平均概率的不可约马尔可夫链的拓扑状态。I(t)是一个具有潜在拓扑状态的控制空间的控制决策变量。

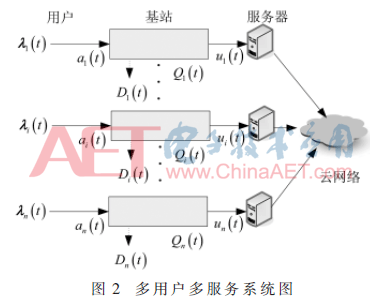
    C(I(t)，S(t))={C_ab(I(t)，S(t))|a，b∈{1，2，…，N}，a≠b}定义为传输速率函数矩阵，其中C_ab(I(t)，S(t))表示在分配控制I_S和网络拓扑状态S下经过链路(a_l，b_l)的传输速率，它是有界的任意值。

1.2 队列模型

    用Q_n(t)表示在时间间隙t时在第n个节点等待网络服务的队列成员数目，a_n(t)表示第n个节点包括新到达数据和节点间转移数据在内的总的数据，u_n(t)表示在时间间隙t时，第n个节点中获得网络服务的用户数据，则动态队列长度表示式：

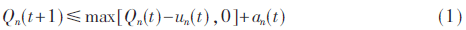
a(t)=(a₁(t)，a₂(t)，…，a_n(t))和u(t)=(u₁(t)，u₂(t)，…，u_n(t))表示是随机事件的一般函数。表示随机事件w(t)的一般函数表达式及一个控制行为表达式为α(t)：α_n(t)=a_n(α(t)，w(t))。每个时隙中由网络控制器观察w(t)并选择合适的α(t)∈A_w(t)，A_w(t)表示与事件w(t)的控制空间集。李雅普诺夫漂移是一种有助于网络队列稳定并进行稳定的控制的有效数学工具，利用负李雅普诺夫漂移理论，在马尔可夫链中可以形成一个成熟的的稳定理论。

    定理1：队列被称为强稳定，如果有：

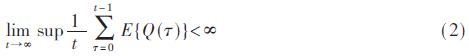
    即如果队列有一个有界的时间平均累积，则该队列强稳定。

    定理2：如果网络中所有独立队列是强稳定的，则网络是强稳定的。

    本文假设满足以下条件时，系统是稳定的：

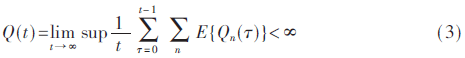
1.3 问题的定义

    系统的目标是找到一个资源分配和调度方案，最大化减少队列的延迟和长度，该问题表示为：

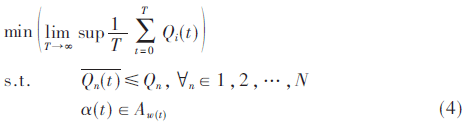
2 高稳定性动态资源管理方案

2.1 动态背压资源管理框架

    如图3所示，对任一节点n，其队列模型包括：新到的数据λ_n，转移数据D_n，队列长度Q_n，网络服务量u_n。在多个节点的队列的基础上进行无线资源的分配，时间间隙t表示时间为[t，t+1)。所有的节点都会存在新到用户数据，且相互独立。而转移用户数据则与节点及其相邻节点的数据流量有关，新到数据服从泊松分布，且E[λ_n(t)]=λ_n。由此根据不同的节点流量，可以将动态队列分为以下3种情况：

    (1)节点只有新到数据，没有转移数据，则队列为Q_n(t+1)=max[Q_n(t)-u_n(t)，0]+λ_n(t)，a_n(t)=λ_n(t)；

    (2)节点流量较大，会转移部分数据D_n(t)到相邻节点，Q_n(t+1)=max[Q_n(t)-u_n(t)，0]+λ_n(t)-D_n(t)，a_n(t)=λ_n(t)-D_n(t)；

    (3)节点流量较小，会从相邻的节点中得到部分数据D_n(t)，Q_n(t+1)=max[Q_n(t)-u_n(t)，0]+λ_n(t)+D_n(t)，a_n(t)=λ_n(t)+D_n(t)。

    (1)选择合适的资源控制I(t)策略来优化如下目标：

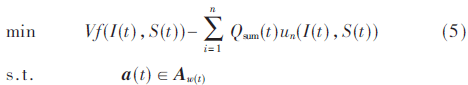
    根据各节点的队列长度和服务速率，使用改进的匈牙利算法来实现更好的效用匹配。

    (2)根据式(4)即时更新队列数据。

    首先介绍背压控制策略w_n(t)。假设w_n(t)表示是一个概率分布为π(w)的平稳过程，w_n(t)在集合Ω中取值，对任意w_n(t)∈Ω，π(t)表示关联队列长度Q_n(t)和到达数据a_n(t)的概率函数，且：

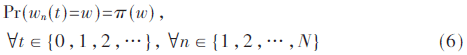
    除了队列需要稳定的Q_n(t)，本文也使用一个辅助的随机相关量y(t)，它的时间平均值会小于或接近特定值y^*，假设y(t)的下界为y_min，因此任意时隙以及任何可能的分配控制策略都会存在E{y(t)}≥ymin。

    定理3：假设有L(Q(t))，y_min，E[L(Q(0))]<∞，则存在常数B≥0，V≥0，?着≥0和y_min，使得对任意时隙和所有的队列值，有：

2.2 针对多队列的李雅普诺夫漂移技术

2.3 针对资源分配的改进匈牙利算法

    将a_n(t)和Q_n(t)视为由w_n(t)控制的配对问题，配对问题由U和V两部分组成，以及带有权重的边集合E。假定a_i(t)∈V，i∈1，2，…，N，Q_j(t)∈U，j∈1，2，…，N，则x_ij为n×n单位阵。假设在一个时隙内一个用户终端只能与一个基站相连接，即表示对相同的边矩阵任一行列中仅有一个值为1，通过匈牙利算法来调制x_ij以匹配相应的a_n(t)和Q_n(t)来实现：

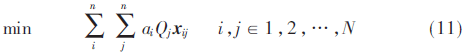
3 仿真实验

    仿真中，有5个节点和充足的用户终端数据。在没有突发数据到达的情况下，新到达的数据服从泊松分布，到达速率均为λ=2/3；在有突发数据到达的情况下，新到数据同样服从泊松分布，且速率也为λ=2/3，只是在某一时间节点会到达大量的用户数据。先到先服务是队列成员获得网络服务的准则，各信道状态S(t)在同一时隙相互独立，且其概率设定为20%。各节点的服务速率是固定的，网络的总服务速率为r=1，为了计算简便，假定各节点的最大容量均为10，并给定相应的服务质量标准。

    本文做了两种不同场景下的仿真，在第一种场景中，用户终端数据随机到达5个节点，由此可以得到某一时隙网络的总效用结果；在第二种场景中，200个用户终端数据到达一个节点，由此可以得到某一时隙节点的平均开销结果和队列长度。本文将所提出的方案与随机分配策略、最短优先策略和比例公平策略进行了对比，且在第二种场景中，当V=25时，设定不同的突发用户数据量，仿真结果如图4～图6所示。

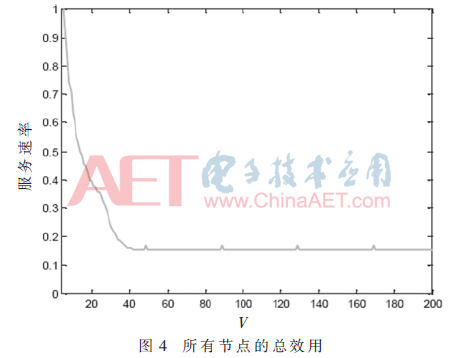
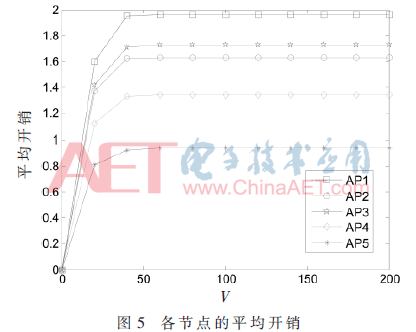
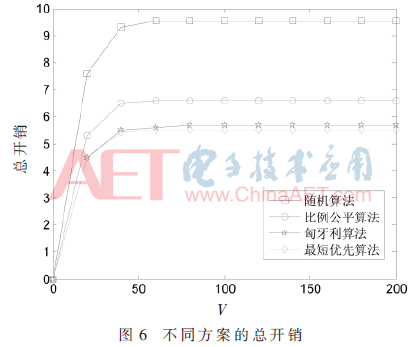
    图4给出了第一种场景下的仿真结果，从图中可以看出，当V接近40时，队列趋于稳定。

    图5给出了没有突发用户数据的场景，设节点服务率r(AP5)>r(AP4)>r(AP3)>r(AP2)>r(AP1)，且r(AP3)比r(AP2)略大。从图5可以看出，当V∈[35，50]时，各个用户队列趋于稳定，节点的服务速率越大，队列稳定的越快。然而，尽管AP3的服务速率比AP2略高，AP3的平均开销却比AP2要低一些，这表明平均开销并非仅由节点服务速率决定。当队列趋于稳定后，各节点队列的平均开销依然维持在较低值。

    图6给出了没有突发用户数据场景下不同方案的总开销，结果表明本方案中队列会更快趋于稳定，且有更低的开销，比随机分配策略和比例公平策略要好，仅次于最短优先策略。

4 结论

    本文研究异构的资源管理问题，重点分析了拥挤用户时的队列稳定性问题，以及用户对无线资源的需求，并提出了一种新的高稳定的动态资源管理方案。与其他研究不同之处是，本文假定各节点的容量是有限的，并进而提出了一种新的用户队列模型，在此基础上，分析了两种不同场景下的资源管理问题并进行了仿真实验。仿真结果表明，本文基于李雅普诺夫漂移和匈牙利算法的异构云无线接入网络资源管理方案，相较于传统的随机分配、比例公平以及最短有限方案而言，在队列的稳定性以及开销上有更好的性能。

参考文献

[1] BLAU I，WUNDER G，KARLA I.Decentralized utility maximization in heterogeneous multicell scenarios with interference limited and orthogonal air interfaces[J].EURASIP Journal on Wireless Communications and Networking，2009，20(12)：104-116.

[2] SHEN W，ZENG Q.Resource management schemes for multiple traffic in integrated heterogeneous wireless and mobile networks[C].Proceedings of 17th International Conference on Computer Communications and Networks，US Virgin Islands，2008：1-6.

[3] PEI X，JIANG T，QU D，et al.Radio resource management and access control mechanism based on a novel economic model in heterogeneous wireless networks[J].IEEE Transactions on Vehicular Technology，2010，59(6)：3047-3056.

[4] NIYATO D，HOSSAIN E.Bandwidth allocation in 4G heterogeneous wireless access networks: A non cooperative game theoretical approach[C].Proceedings of IEEE Global Telecommunications Conference，San Francisco，CA，2006：1-5.

[5] TAO M，LIANG Y C，ZHANG F.Resource allocation for delay differentiated traffic in multiuser OFDM systems[J].IEEE Transactions on Wireless Communications，2008，7(6)：2190-2201.

[6] BHATTACHARYA P，GEORGIADIS L，TSOUCAS P.Adaptive lexicographic optimization in multi-class M/GI/1 queues[J].Math.Operat.Res.，1993，18(3)：705-740.

[7] RADUSINOVIC I，PEJANOVIC M，PETROVIC Z.An ILPF cell scheduling algorithm for ATM input-queued switch with service class priority[C].Proceedings of 6th International Conference on Telecommunications in Modern Satellite，Cable and Broadcasting Service，2003，1：26-29.

[8] KUMAR P R，MEYN S P.Stability of queueing networks and scheduling policies[J].IEEE Transactions on Automatic Control，1995，40(2)：251-260.

[9] ANDREWS M，KUMARAN K，RAMANAN K，et al.Providing quality of service over a shared wireless link[J].IEEE Commun.Mag，2001，39(2)：150-154.