0 引言

　　由于人为调制等原因，大多数雷达和通信信号都体现出一种特殊的周期性，即循环平稳特性，不同调制样式的信号具有不同的循环平稳特性[1]，因此，基于信号循环平稳特性的参数估计方法在信号的选择性和噪声抑制方面具有显著优势[2]。

　　阵列信号处理是信号循环平稳特性成功应用的一个典型例子[2]。GARDNER W A首先把信号的循环平稳特性引入到阵列测向方法中，提出了相应的Cyclic MUSIC（简记为C-MUSIC）方法[3]。文献[4，5]分析了C-MUSIC方法对高斯和非高斯窄带循环平稳信号测向的性能，但该分析都是基于理想阵列结构进行的。随后，CHARGE P等通过综合考虑入射信号的循环相关函数和共轭循环相关函数，对已有的C-MUSIC方法进行了扩展，提出了Extended Cyclic MUSIC（简记为EC-MUSIC）方法[6]。与C-MUSIC方法相比，EC-MUSIC方法更有效地利用了入射信号的信息，因此具有更优的测向性能。当入射信号带宽较为显著时，YAN H对C-MUSIC方法进行了修正，提出了Improved Cyclic MUSIC方法[7]，极大地减小了实际信号的非零带宽在C-MUSIC方法中所带来的测向偏差。该修正思想同样可用于EC-MUSIC方法中，借以减小对非零带宽近似窄带信号的测向偏差[7]。

　　在实际系统中，接收阵列可能存在各种模型误差，如阵列互耦、通道不一致性等。当此类误差存在时，C-MUSIC方法和EC-MUSIC方法可能产生测向偏差。本文以常规阵列中很难消除的阵列互耦效应为对象，通过建立互耦条件下Cyclic MUSIC方法和EC-MUSIC方法的伪数据模型，考查这两种方法的测向性能受互耦效应的影响情况，给出了均匀线阵和一般线阵中测向偏差的解析表达式，并通过仿真实验验证了信号入射方向和阵元间距变化时该理论偏差的准确性。

1 互耦条件下窄带循环平稳信号测向方法的伪数据模型

　　假设K个循环频率为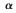的窄带信号从不同方向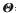=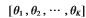同时入射到M元均匀线阵上，则阵列接收数据模型为：

　　其中x(t)=[x1(t)，x2(t)，…，xM(t)]T为阵列在t时刻的接收数据构成的向量，s(t)=[s1(t)，s2(t)，…，sK(t)]T为各入射信号在t时刻的波形，A(f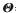，)=为第k个信号在相邻阵元间的传播时延）为K个信号的导向矢量，为表述方便，以下的讨论中简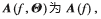记并特别标记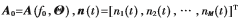为阵列加性噪声。另外，记信号sk(t)的幅度包络为gk(t)，即sk(t)=。

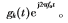　　互耦条件下阵列观测数据为[8]：

　　其中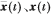分别为互耦条件下和理想情况下t时刻阵列的接收数据，C为阵列互耦矩阵。在以下的叙述中，如无特别说明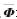，均表示变量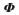在互耦条件下的取值。

　　第p个阵元t时刻的接收数据为：

　　其中cpu为C的第(p，u)个元素。

　　1.1 互耦条件下C-MUSIC方法的伪数据模型

　　互耦条件下第p个阵元和第q个阵元接收数据的循环互相关函数为：

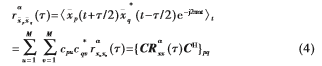
　　其中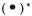为共轭运算符，为共轭转置运算符，且：

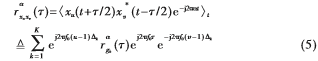
　　进一步地，其中，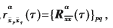

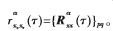
　　结合文献[3]给出的无互耦伪数据矩阵，得到互耦条件下考虑窄带信号非零带宽时的阵列伪数据矩阵为：

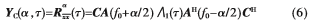
　　其中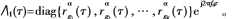

　　1.2 互耦条件下EC-MUSIC方法的伪数据模型

　　经过类似的推导，得到互耦条件下第p个阵元和第q个阵元接收数据的共轭循环互相关函数为：

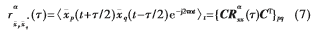
　　因此，其中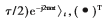为转置运算符。

　　进而得到互耦条件下EC-MUSIC方法的阵列伪数据矩阵为：

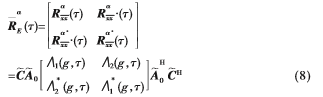
　　其中，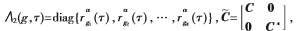 

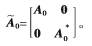
　　结合文献[6]给出的理想情况下EC-MUSIC方法的伪数据矩阵，得到互耦条件下考虑窄带信号非零带宽时的阵列伪数据矩阵为：

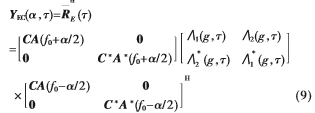
2 互耦条件下C-MUSIC方法的测向误差分析

　　对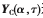进行特征值分解，得到互耦条件下C-MUSIC方法的信号子空间和噪声子空间：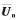

　　结合式(6)、式(10)不难看出，信号子空间与真实信号方向矩阵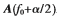之间存在如下关系：

　　其中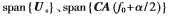分别表示由矩阵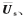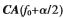的各列所张成的子空间。

　　如果互耦条件下，空间多个目标仍然可以分辨，则由空间谱函数：

　　估计得到的信号波达方向所构成的阵列导向矢量与真实导向矢量间满足如下关系：

　　a

　　其中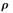为幅度调整系数。

　　记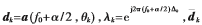和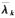为相应的互耦条件下对应的变量。由互耦条件下阵列接收数据的循环互相关协方差矩阵的特征值分解得到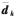的估计值之后，可用如下罚函数确定

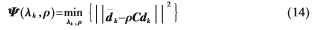
　　参考文献[9]中的数学推导，可以由以上罚函数得到互耦条件下对第k个信号角度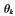的估计误差为：

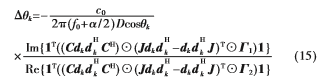
　　其中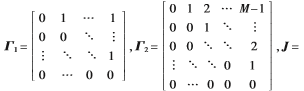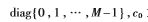为电磁波传播速度，1为全1列向量，其维数由上下文确定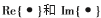，分别为复数的实部和虚部，⊙表示矩阵或向量点乘运算符。

3 互耦条件下EC-MUSIC方法的测向误差分析

　　对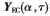进行特征值分解，得到互耦条件下EC-MUSIC方法中伪数据协方差矩阵的信号子空间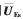和噪声子空间：

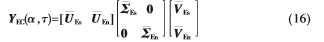
　　互耦条件下波达方向的估计结果由如下空间谱估计函数得到[6]：

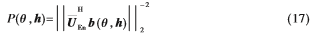
　　其中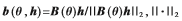，表示取L2范数，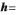

　　为了消除加权向量h的影响，将上述空间谱函数转化为：

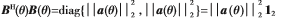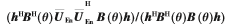　　由于为二阶单位矩阵乘以系数，因此当h等于矩阵的最小特征值对应的特征向量时，取最小值，且该最小值等于矩阵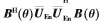的最小特征值。定义该矩阵为E，则：

　　由于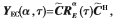因此：

　　其中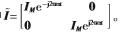

　　经过类似参考文献[6]附录中的推导过程可以得到结论：进而有：

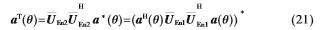
　　因此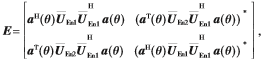，该矩阵的最小特征值为：

　　最终的空间谱函数为：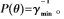

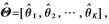　　通过搜索的峰值可以得到信号波达方向的估计值由于：

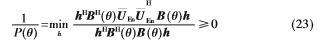
　　因此

　　同时，观察的特征分解式(16)不难看出：

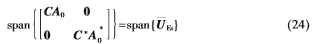
　　故

　　所以，当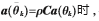有：

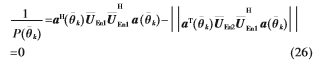
　　进而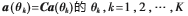即空间谱函数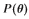的峰值出现在满足式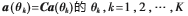处，即：

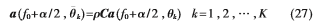
　　其中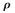为幅度调整系数。

　　由阵列接收数据的循环互相关协方差矩阵的特征值分解得到的估计值之后，可用如下罚函数确定：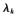

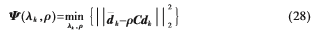
　　经过一系列的数学推导[9]，可以由以上罚函数得到互耦条件下对第k个窄带循环平稳信号的入射角度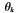的估计误差为：

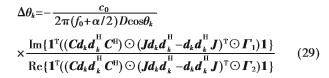
4 仿真

　　为了验证以上理论分析结果的正确性，在以下的实验中均假设一个远场BPSK信号入射到均匀线性阵列上，并假设窄带接收阵列由多个细线偶极子天线沿x轴排列而成。信号带宽与载波频率之比为0.02，可近似看作窄带信号，但为了减小非零带宽给窄带循环平稳信号测向模型所带来的误差，测向方法选择Improved Cyclic MUSIC及其扩展形式。阵列的阻抗由开环计算方法得到[10]，细线偶极子天线之间的阻抗参考文献[11]进行计算。

　　(1)实验1：假设一个相对带宽为2%的BPSK信号入射到8元均匀线阵上，相邻阵元间距等于半波长，仿真得到C-MUSIC方法、EC-MUSIC方法的角度估计偏差和由式(15)、式(29)给出的均匀线阵的理论偏差的对比情况如图1所示。

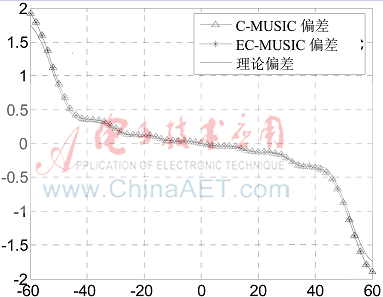
图1  互耦条件下均匀线阵的测向偏差随信号入射方向的变化情况

　　(2)实验2：在实验1的基础上保持信号入射方向为20°，相邻阵元间距从0.1倍波长到半波长之间变化，仿真得到C-MUSIC方法、EC-MUSIC方法的角度估计偏差和由式(15)、式(29)给出的均匀线阵的理论偏差的对比情况如图2所示。

图2  互耦条件下均匀线阵的测向偏差随相邻阵元间距的变化情况

　　上述仿真结果表明，在阵列互耦效应存在的情况下，本文所得到的窄带循环平稳信号阵列测向方法及其共轭扩展方法的测向偏差的理论结果都具有较高的准确度，很好地反映了两种方法的测向误差随信号入射方向和阵列结构的变化情况。

5 结束语

　　本文通过分析互耦条件下窄带循环平稳信号测向方法C-MUSIC以及EC-MUSIC的伪数据矩阵模型，借助数学分析得到了这两种方法的测向偏差受互耦效应影响情况的解析表达式，并借助仿真实验验证了所得理论偏差的准确性。该解析结果对阵列误差条件下窄带循环平稳信号阵列测向方法的性能分析以及实际系统的误差校正都具有较强的指导意义。

　　参考文献

　　[1] GARDNER W A.Signal interception:A unifying theoretical framework for feature detection[J].IEEE Transactions on Communications，1988，36(8)：897-906.

　　[2] GARDNER W A，NAPOLITANO A，PAURA L.Cyclostationarity：Half a century of research[J].Signal Processing，2006，86(4)：639-697.

　　[3] GARDNER W A.Simplification of MUSIC and ESPRIT by exploitation of cyclostationarity[J].Proceedings of the IEEE，1988，76(7)：845-847.

　　[4] SCHELL S V，GARDNER W A.The Cramer-Rao lower　bound for directions of arrival of Gaussian cyclostationary signals[J].IEEE Transactions on Information Theory，1992，38(4)：1418-1422.

　　[5] SCHELL S V.Performance analysis of the cyclic MUSIC method of direction estimation for cyclostationary signals[J].IEEE Transactions on Signal Processing，1994，42(11)：3042-3050.

　　[6] CHARGE P，Wang Yide，SAILLARD J.An extended cyclic MUSIC algorithm[J].IEEE Transactions on Signal Processing，2003，51(7)：1695-1701.

　　[7] YAN H，FAN H.On improvements of cyclic MUSIC[J].Eurasip Journal on Applied Signal Processing，2005，50(1)：61-68.

　　[8] YEH C，LEOU M，UCCI D.Bearing estimations with mutual coupling present[J].IEEE Trans.on Antennas and Propagation，1989，37(10)：1332-1335.

　　[9] LIU Z，HUANG Z，ZHOU Y.Bias analysis of MUSIC in the presence of mutual coupling[J].IET Signal Processing，2009，3(1)：74-84.

　　[10] GUPTA I，KSIENSKI A.Effect of mutual coupling on the performance of adaptive arrays[J].IEEE Trans.Antennas Propagat.，1983，9(31)：785-791.

　　[11] JOHN D，RONALD J.Antennas：for all applications[M].3rdedn.McGraw-Hill Company，2002.