余景鹏，李姣军，陶金，贾智予
(重庆理工大学 电子信息与自动化学院，重庆 400054)
摘要：为了克服小波阈值去噪中硬阈值小波系数不连续和软阈值估计小波系数与分解小波系数之间恒定偏差的缺点，改进的阈值去噪方法被相继提出。文章根据高斯白噪声和信号在小波变换以后得到的小波系数呈现不同的特性，基于噪声方差提出一种新算法。最后通过MATLAB仿真验证该算法在信噪比、均方根误差、相关系数、信噪比增益4个去噪指标的效果。
关键词：小波阈值;小波变换；噪声方差；去噪指标
0引言
信息在采集传输过程中，由于各种人为或者非人为因素，获得原始信号中不可避免地包含噪声，而噪声往往会影响信号质量［1］，因此得到比较纯净的信号一直以来是人们追求的目标。
随着技术和社会的不断进步，各种不同去噪方法相继出现，有纯时域、纯频域、中值滤波、傅里叶变换、短时傅里叶变换等方法。小波理论［2］是最近几十年兴起的一门重要学科，小波变换具备良好的时频局部特性、多分辨率、低熵性、去相关性和选基灵活性［3］ 等优点而受到许多学者重视，小波分析在许多领域得到广泛应用。
目前小波去噪常用的方法有相关性去噪、模极大值去噪、平移不变量去噪和小波阈值去噪［4］，其中小波阈值去噪是一种实现简单、效果较好的去噪方法。
1去噪原理
有用信号一般是低频或者是平稳的，噪声信号一般是高频或者是非平稳的［5］。小波变换得到高频系数和低频系数，通常认为高频系数来自于噪声信号，所以一般阈值处理都是对高频系数而言。
假设一维信号含噪模型为［6］：
式中,s(t)为含噪声的信号，x(t)为原始信号，u(t)为标准的正态分布，均值为0，方差为1。由于小波变换是线性变换，对含噪信号做离散小波变换，得到的小波系数由两部分组成，低频系数一般由有用信号贡献，高频系数一般由噪声产生。
小波阈值去噪的一般步骤［7］：
（1）选定小波基和分解层数，然后对含噪信号进行小波变换得到小波系数Wj,k。
（2）选择一个适当的阈值并对得到的小波系数Wj,k进行相应的阈值处理，得到估计小波系数W~j,k。
（3）得到处理后的估计小波系数后进行小波重构，得到比较纯净的信号。
小波阈值去噪一般要注意的问题是小波基的选择、分解层数的确定、阈值函数、阈值规则确定阈值。其中较为关键的一步是阈值的选取。选择合理的阈值可以得到良好的去噪效果，阈值选择比较小，重构得到的信号噪声比较多；反之，重构得到的信号会丢失一部分有用信号。
小波阈值收缩法是DONOHO D L和JOHNSTONE I M［2］在1992年提出的,其理论依据是,小波变换使信号的能量集中在一些大的小波系数中，而噪声的能量却分布于整个小波域内。随着分解层数的增加有用信号的小波系数增大，而噪声的小波系数减小。有用信号的小波系数幅度一般要大于噪声的系数幅度。所以在采用阈值去噪时可以把噪声系数收缩或者置为零，从而达到去噪效果。
常见的硬阈值和软阈值函数分别如式（2）和（3）：
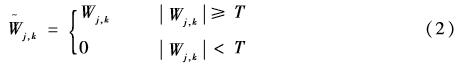
其中，
为阈值，噪声高频系数标准差
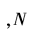为信号的长度。
从上面的两个分段函数可以看出，硬阈值函数在阈值点处是不连续的，重构信号存在伪吉布斯现象［8］。软阈值函数估计小波系数与原来的小波系数总存在着恒定的偏差,信号重构逼近不能达到预期效果［9］。因此,许多研究者寻找新阈值函数（改进阈值函数）都是基于上述硬阈值和软阈值函数以及两者缺点。
针对上述硬阈值和软阈值函数的缺点，基于概率论知识以及小波变换后信号能量集中在少数幅度较大系数上，提出一种新算法。该算法的具体步骤如下：
（1）选定小波基和分解层数进行小波分解，计算噪声标准差和各层高频系数的标准差。
（2）首先判断第1层的高频系数与噪声系数标准差大小，如果高频系数标准差大于噪声标准差，选取高频系数最大值并且置位零记下其相应的下标；如果高频系数噪声小于噪声方差则执行一步就跳出转到步骤（5）。
（3）得到新的高频系数继续与噪声方差作比较，重复第（2）步，直到高频系数的方差小于或者等于噪声方差则退出循环。得到每次的最大值组成一个新的高频系数。
（4）第2层、3层…J层依次重复步骤（2）、（3），得到各层高频系数。
（5）得到各层高频系数和低频系数后进行小波重构，然后计算去噪指标。
2去噪评价
目前常用的去噪评价方法有两种：主观评价法和客观评价法［3］。主观评价法在噪声差别很明显的情况下很容易辨别出来，而在去噪以后差别不是很大的情况下会受人为的影响，得到的效果往往不如人意，结论往往会带有一定的主观色彩。客观评价法具有一定质量指标体系，通过不同的指标来判定去噪以后的效果，单个指标很难衡量去噪效果，所以人们一般通过多个指标来衡量，而不同的问题实际情况不一样所以指标不一样。因此在实际问题中，经常将主观与客观两种方法相结合。常用的去噪性能评价指标主要有以下几种：
（1）信噪比（SNR）:原始信号的能量与噪声能量之比。
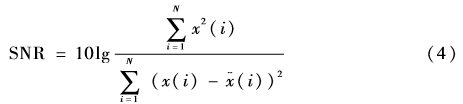
其中，x(i)为原始信号，x~(i)为去噪以后的信号（以下均同），N为信号长度。一般认为信噪比越大去噪效果越好。
（2）均方根误差（RMSE）［4］:是指去噪以后信号与原始信号差的平方和与信号长度N比值的平方根。
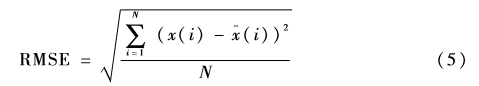
均方根误差越小表示去噪效果越好。
（3）互相关系数（ρ）［4］ : 表示信号之间相似度。
其中，cov（x(i),x~(i)）表示两个信号之间的协方差， D(x(i))为原始信号的方差， D(x~(i))为去噪后信号的方差。互相关系数越接近1表示去噪效果越好。
（4）信噪比增益（GSNR）［4］:指小波去噪后的信噪比与去噪前的原始信噪比的比值。
其中，SNRo表示输出信噪比，SNRi表示输入信噪比，一般认为信噪比增益越大则去噪效果越好。
3仿真结果与分析
实验过程采取blocks信号信噪比(SNR)为15.424的含噪信号和doppler信号信噪比（SNR）为12.028的含噪信号，信号和噪声是线性叠加的，高斯白噪声方差为1、均值为0。用‘db2’小波对信号进行3层分解。分别应用本文算法、强制消噪（得到高频系数全部置位零）、硬阈值和软阈值4种方法进行仿真，然后比较4个指标结果。结果如图1、图2所示。
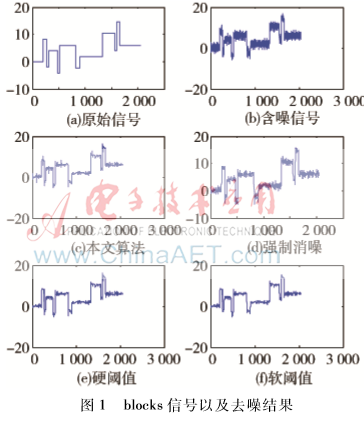
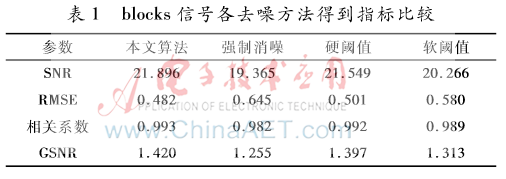
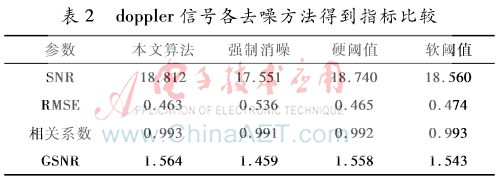
从图1和图2很容易看出，强制去噪效果不是很好，有用信号可能淹没在噪声中。而硬阈值和软阈值与本文算法观察图形比较，不能很容易区分哪个去噪效果较好，主观评价方法显得有点无能为力。在此情况下只能用客观评价法，通过信噪比、均方根误差、相关系数、信噪比增益来比较去噪效果。由上述指标介绍可知信噪比和信噪比增益越大、均方根误差越小、相关系数越接近1则表示去噪效果越好，本文通过4个指标的计算来验证不同去噪方法的效果，避免单个指标衡量存在的偶然性，更具有一定的有效性。通过表1和表2可以看出，本文算法具有一定的优越性。
4结束语
小波变换后低频和高频系数来源不同，依据高斯白噪声正态分布来调整高频系数，提出一种新的阈值去噪算法，仿真结果表明该算法优于其他常用算法。
参考文献
［1］ DONOHO D L. Denoising by softthreshold［J］.IEEE Trans on IT,1995,41(3):613 627.
［2］ DONOHO D L, JONSTONE I M.Adapting to unknown smoothness via wavelet shrinkage［J］.Journal of the American Statistical Association,1999,90(432):1200 1224.
［3］ 潘泉,孟晋丽,张磊,等.小波滤波方法及应用［J］.电子与信息学报,2007， 29(1):236 242.
［4］ 陶珂.小波去噪质量评价方法研究［D］.长沙：中南大学,2012.
［5］ DONOHO D L, JOHNSTONE I M. Ideal spatial adaptation by wavelet shrinkage［J］. Biometrika,1994,81(3):425 455.
［6］ 唐晓初.小波分析及其应用［M］.重庆:重庆大学出版社,2006.
［7］ 彭园园.小波分析在一维信号去噪中的应用［D］ 北京：北京邮电大学, 2011.
［8］ 韦力强.基于小波变换的信号去噪研究［D］.长沙：湖南大学,2007.
［9］ 张臣国. 小波分析在信号降噪中的应用研究［D］.成都：电子科技大学,2012.