文献标识码: A
DOI:10.16157/j.issn.0258-7998.2016.11.021
中文引用格式: 许爱东,黄文琦,陈华军,等. 基于模糊神经和局部统计的变压器故障研究[J].电子技术应用,2016,42(11):80-83,87.
英文引用格式: Xu Aidong,Huang Wenqi,Chen Huajun,et al. FDI research of power transformers based on fuzzy neural and local statistical method[J].Application of Electronic Technique,2016,42(11):80-83,87.
0 引言
随着电力系统自动化的快速发展以及特高压电网的大规模建设,需要转变现有的调度运行模式,尤其是提高电网状态监测和故障诊断隔离(Fault Detection and Isolation,FDI)的智能化水平。因此,推动电网运行逐步向自动化、集中化、智能化方向发展成为了必然趋势[1]。电力变压器作为电网传输、调度和配电系统中最昂贵和重要的设备之一,对其状态的监测对电网运行的持续性和可靠性具有重要意义[2]。考虑到变压器没有FDI系统,在其接近负载极限工况运行时,会存在重大的安全及环境风险。而对其状态和老化性能提供明确的实时评估,可以避免不可逆的故障,并提供预防性维护。目前许多学者建立电力变压器高精度温度模型,由于负载电流分布、顶层油温和天气条件(环境温度、太阳能加热、风速、降雨条件等)都是影响电力变压器温度性能因素,其存在复杂的不确定性,难以建立精确的模型[3]。结合上述文献,对电力变压器状态及相关的故障风险可通过监测的热点温度(High Spot Temperature,HST)进行评估,HST在预期温度分布中的偏差可用作对电力变压器老化或其他可能故障的评估指标,并将HST与相关输入等相关联,建立基于神经网络的HST数值分析模型[4]。此外,可将无故障状态下电力变压器温度模型与实际变压器在线测量输出比较分析,实现对电力变压器故障检测和隔离。局部统计法是统计变压器故障检测和隔离的常用方法,可以结合两者之间的关系,设计评估指标[5]。通过该方法可将电力变压器FDI的复杂检测问题转化为一个高斯向量的平均值监测问题。
1 电力变压器监测和故障分析
1.1 变压器热模型
为了更好地分析电力变压器工作状态,建立了其动态温度模型,步骤如下[6]:
(1)通过检测每个时刻的负载电流,计算对应顶层油温变化:

(2)结合每一个采样周期的最终顶层油温变化值和环境温度,计算顶层油温的增加量如下:

尽管式(1)~式(5)中提出了顶层油温变化简化模型,分析温度模型机理,但其准确性受模型的参数影响较大,且参数不定。因此需要构建更为精确的自适应模型,以保证变压器选取更为合适的热点温度。
1.2 变压器老化
通常将变压器的老化分成两种类型,一种是不可预防的老化,主要是绝缘材料自身引起的老化;另一种是可预防性的老化,主要是不正常操作方式导致。后者通常可以通过监测和报警的方式,及时改变变压器的工作模式,需要合理做出变压器的工作寿命和传输效率之间的取舍。通常将引进安全影响因子来评估变压器老化和故障指数,但是难以建立精确的表达式,因此自适应算法成为了解决该类问题的热点[7]。
1.3 模糊神经模型
传统的数学建模难以保证变压器的模型精度,模糊神经作为常用的辨识和故障诊断自适应方法广泛应用于复杂非线性系统[7]。本文提出了一种基于模糊神经的热点温度模型,监控变压器的热点温度情况,并结合如下的Takagi-Sugeno-Kang(TSK)模糊规则:

2 故障诊断隔离方法
2.1 全局χ2检验方法
在电力变压器工作正常时,提取其实际的输入输出数据,训练得到无故障状态的变压器模糊神经模型。为了使得变压器模糊神经模型和故障提取模型拥有相同数目的参数,该故障提取模型同样通过电力变压器的输入输出数据得到对应的精确模型。模糊神经模型模拟电力变压器在无畸变状态,故障诊断模型模拟实际电力变压器工作状态,两者必然会出现残差ei。即故障诊断模型的输出为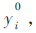 模糊神经模型的输出为yi,则
模糊神经模型的输出为yi,则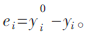 对该残差的平方求偏导如下:
对该残差的平方求偏导如下:

式中,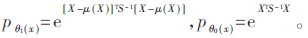 此时,发生故障系统的高斯分布中心值为μ(X)=Mη。通过最小化关于η的似然比,可得到广义似然比,意味着已经考虑到最有可能发生参数变化情况,可给出如下的全局χ2检验:
此时,发生故障系统的高斯分布中心值为μ(X)=Mη。通过最小化关于η的似然比,可得到广义似然比,意味着已经考虑到最有可能发生参数变化情况,可给出如下的全局χ2检验:

2.2 最小最大检验方法

3 仿真实验
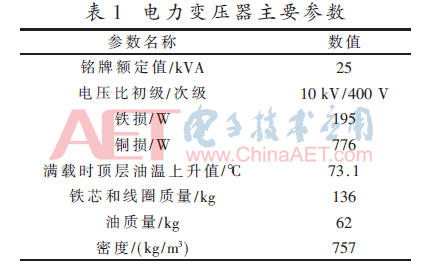
首先在电力变压器工作正常时得到模糊神经模型和变压器实际输出的残差序列,作为变压器实际输出和模糊神经模型输出之间的无故障参考模型。然后假设系统中某些参数变化,通过计算残差序列的似然比,判断变压器故障情况。变压器的主要参数如表1。
利用模糊神经网络对变压器进行数学建模,模型输入包含顶层油温之前值和负载电流值,如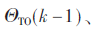
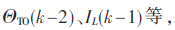 模型输出为估计的热点温度
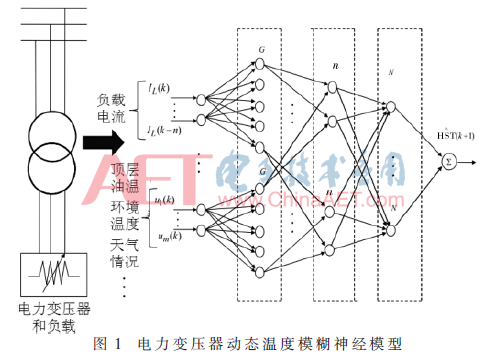
模型输出为估计的热点温度 对应故障隔离模型的输入输出和模糊神经模型一致。在第一种情况下,由于Hermite多项式基函数具有多频特性,构建的模型拥有捕捉热点分布的精度和突变的优点,用于模拟电力变压器热点温度变化的模型。在第二种情况下,设计如图1的TSK型模糊神经模型。将输入空间利用输入维数划分法分割,以提高模型的计算效率和辨识精度。Hermite多项式基于函数神经网络和TSK型模糊神经模型训练的最小均方根误差均为4×10-3,对应的训练集数据量是300个,并利用最小均方差算法调节线性模型的权值
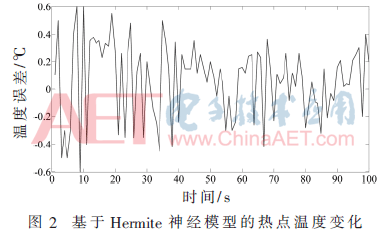
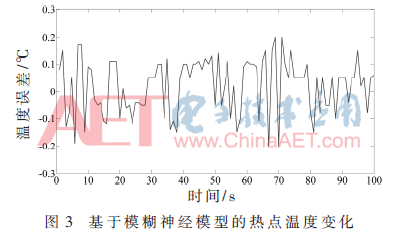
对应故障隔离模型的输入输出和模糊神经模型一致。在第一种情况下,由于Hermite多项式基函数具有多频特性,构建的模型拥有捕捉热点分布的精度和突变的优点,用于模拟电力变压器热点温度变化的模型。在第二种情况下,设计如图1的TSK型模糊神经模型。将输入空间利用输入维数划分法分割,以提高模型的计算效率和辨识精度。Hermite多项式基于函数神经网络和TSK型模糊神经模型训练的最小均方根误差均为4×10-3,对应的训练集数据量是300个,并利用最小均方差算法调节线性模型的权值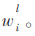 该模糊神经模型包含64个模糊规则(在4个模糊子集中分别化分出3个输入变量)。基于TSK模糊模型的64个子集数据来源于实际电力变压器的热点温度、顶层温度和负载电流数据。模型包括64个线性参数(权值wi)和12个非线性参数(模糊集的中心值ci)。该模型的模糊规则可缩减到27个,降低了模型的计算复杂度。缩减后形成新的TSK模糊模型的参数有39个(27线性参数为输出层权值和12非线性参数为模糊集的中心值)。将局部统计法应用在FDI中,以及在变压器模型中应用χ2变化检测检验,对应的故障诊断阈值应该设定为39。如图2和图3,模糊较Hermite神经模型的精度高出2倍多,完全适用于变压器热点温度的变化模型。
该模糊神经模型包含64个模糊规则(在4个模糊子集中分别化分出3个输入变量)。基于TSK模糊模型的64个子集数据来源于实际电力变压器的热点温度、顶层温度和负载电流数据。模型包括64个线性参数(权值wi)和12个非线性参数(模糊集的中心值ci)。该模型的模糊规则可缩减到27个,降低了模型的计算复杂度。缩减后形成新的TSK模糊模型的参数有39个(27线性参数为输出层权值和12非线性参数为模糊集的中心值)。将局部统计法应用在FDI中,以及在变压器模型中应用χ2变化检测检验,对应的故障诊断阈值应该设定为39。如图2和图3,模糊较Hermite神经模型的精度高出2倍多,完全适用于变压器热点温度的变化模型。
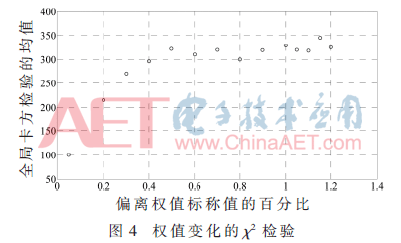
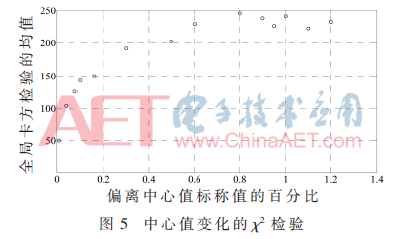
假定电力变压器无故障情况下,基于一系列的试验数据可得到χ2值的均值为38.713,该数值近似等于χ2检测理论期望值。如果电力变压器无故障的参数略有偏离估值时,χ2检测能对相关故障进行报警提示。即便参数的变化值在0.01%~1%之间,?字2检验结果将显著偏离故障阈值。如图4和图5所示,微小的参数变化(小故障)引起的?字2输出多次超过其故障阈值。
最后,基于最小最大法的故障隔离检测也应用在监测电力变压器模型中线性和非线性参数的变化,试验结果表明,最小最大法同样以较高的成功率检测出电力变压器温度模型的故障参数。
4 结论
本文结合电力变压器的故障特点,提出了一种基于模糊神经和局部统计的FDI方法。首先利用模糊神经算法构建电力变压器的温度模型,然后结合优化的全局χ2检验和最小最大的局部统计方法计算对应故障诊断和隔离指标,建立对应FDI的评估机制。仿真结果表明,提出的方法在电力变压器早期FDI中,不但能够对电力变压器故障进行检测、诊断、隔离和预报,而且可有效避免变压器自身噪声对系统性能的影响,实现了对变压器中的关键和昂贵元件预防性维修和保养。
参考文献
[1] 边莉,边晨源.电网故障诊断的智能方法综述[J].电力系统保护与控制,2014(3):146-153.
[2] METWALLY I A.Failures monitoring and new trends of power transformers[J].IEEE Potentials,2011,30(3):36-43.
[3] 曾麟钧,林湘宁,黄景光,等.特高压自耦变压器的建模和电磁暂态仿真[J].中国电机工程学报,2010,30(1):91-97.
[4] 陈伟根,奚红娟,苏小平,等.广义回归神经网络在变压器绕组热点温度预测中的应用[J].高电压技术,2012,38(1):16-21.
[5] ZHANG Q,BASSEVILLE M,BENVENISTE A.Fault detection and isolation in nonlinear dynamic systems:a combined input-output and local approach[J].Automatica,1998,34(11):1359-1373.
[6] IPPOLITO L,SIANO P.Identification of Tagaki-Sugeno-Kang fuzzy model for power transformers predictive overload system[J].IEEE Proc.Gener.Transm.Distribution,2004,151(5):582-589.
[7] NAMBURU S M,AZAM M S,LUO J H,et al.Data-driven modeling,fault diagnosis and optimal sensor selection for HVAC chillers[J].IEEE Trans Automation Science Engineering,2007,4(3):469-473.
[8] ZHANG Q,BASSEVILLE M,BENVENISTE A.Early warning of slight changes in systems[J].Automatica,1994,30(1):95-113.

