0 引言

    J波是一种低幅、高频的变异波形，往往出现在早期复极化综合征和Brugada综合征病人的心电图中，容易导致心率失常和猝死。在最近几年中，针对J波的意义进行了大量研究，J波研究在医电信号领域展现出了新的热点。J波是出现在心电图中QRS波群下降支终点的一个凹口或顿挫^[1]。在心电图中QRS波群和ST段之间的连接处称为J点，J点抬高就会触发J波。标准定义为：当J点和/或ST段从基线抬高至少0.1 mV，持续时间达到20 ms形成的尖峰、驼峰、圆顶形态的波形称为J波^[2]。

    J波与J波综合征有着紧密的联系，J波综合征包括早期复极综合征、特发性室颤和Brugada综合征，这3种综合征有许多共同心电图特征^[3]。每年心血管疾病在世界范围内引起非常高的死亡率，这些死亡率中有很大一部分是由J波综合征引起的。所以，识别J波是预测患者病变结果的一个重要的方向^[4]。换言之，J波的自动识别检测对J波综合征的病人提供了一种非创性的诊断方法。

    为了达到自动检测的目的，本文定义并提取了5个特征向量，其中包括3个时域特征向量和两个基于小波的特征向量，从不同的角度描述了J波的特性，使用这些提取出的、降维的特征向量来训练隐马尔可夫分类器，从而达到自动检测J波的目标。

1 数据准备

    本文构造了一个心电数据库评估提出的方法，这个数据库由2 000个心电信号模式组成，如图1所示，模拟了两个基本的II导联J波阳性模式信号。

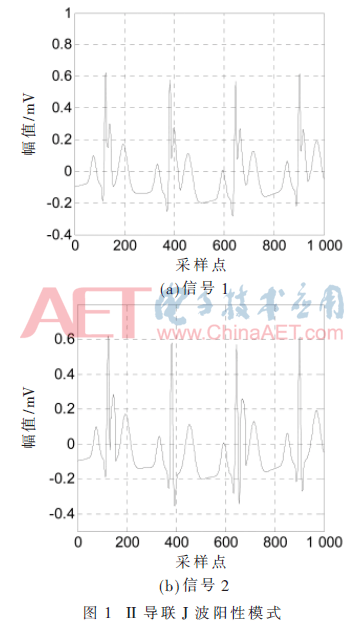
    其中，训练集包括800个心电信号模式，400个为J波阳性心电模式，另外400个为J波阴性心电模式。测试集包含600 个J波阳性心电信号模式和600个J波阴性心电信号模式。

2 方法

    本研究提出的J波自动检测方法，主要是寻找合适的特征增加J波相对于其他心电图成分的区分度。图2为所提出的分类识别J波阳性模式和J波阴性模式的系统框图。

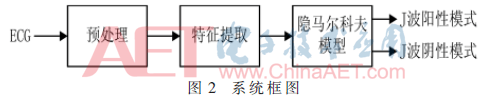
2.1 预处理

    预处理的目的是定位ECG信号的特征点和去噪。主要定位了QRS波群的起点和终点，为下一阶段的特征提取作准备。预处理过程分成3个步骤：

    (1)检测QRS波群起点和R波^[5]。

    (2)利用多拍平均技术提高信噪比。

    (3)定位QRS波群终点。

2.2 特征提取阶段 

2.2.1 时域特征向量I

    J波往往出现在QRS波的下降支，所以选择QRS波群起点后100 ms作为特征向量的提取区域，为了提高检测方法的鲁棒性，同时也考虑了R波前60 ms。这样，提取的时域特征向量覆盖了整个QRS波群下降支部分，可以在这160 ms里面反映了ECG信号的动态变化。由于采样率为500 Hz，选择80个采样点，其中29个在R波之前，50个在R波之后，这样就形成了一个80维的特征向量I，它反映了QRS波下降支的形态学状态。

2.2.2 时域特征向量II

    基于预处理阶段，QRS波群的终点位置已经确定。考虑到J点（连接S波和ST段的连接点）抬高同样会引起J波，所以选择J点后的40 ms作为“监控”对象，同样，考虑到检测方法的鲁棒性，J点前的8 ms也纳入“监控”范围，这样就形成了一个24个采样点组成的时域特征向量II，其中4个点在J点之前，20个点在J点之后。

2.2.3 时域特征向量III

    时域特征向量I和II能从整个形态学上检测ECG的变异。为了能更精细地检测J点之后的形态变化，定义了第3种时域特征向量，把J点前后的48 ms分成4 ms的间隔，求这些间隔的平均值和标准差，这样就形成了一个24维的特征向量。

2.2.4 基于离散小波的特征向量

    Daubechies6（Db6）小波和心电图的形状比较相似，而且在细节上能更准确地反映ECG信号^[6]。因此，选择Db6作为分解ECG的小波。研究已经发现，心电信号的能量主要集中在0.5～40 Hz的频率范围^[7]。应用5级小波分解后，这个频率范围相当于4级细节系数（即D4）和5级细节系数（即D5）以及5级近似系数（即A5）^[8]。

    由于J波频率范围相对集中在4级细节系数(即D4)，本文计算4级细节系数（即D4）幅值统计，从而比较J波阳性模式和J波阴性模式的振幅分布。如图3，从幅值直方图和幅度累积可以看出，两种信号模式的振幅统计有明显的不同，它们可以作为区分两个信号模式的特征。这些系数的幅值统计能够很充分地表达出给定信号模式的频率特性。这样形成了一个30维的基于离散小波变换的特征向量，反映了4级细节系数（即D4）的状态。当J波出现时，D4的幅度分布变化，从这个角度基于离散小波变换的特征向量可以检测有无J波。

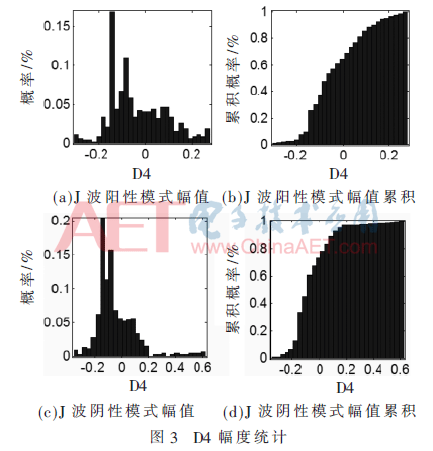
2.2.5 基于连续小波变换的特征向量

    以上几个特征向量已经能从时域和频域对J波发生区域进行检测，但是只是单独地进行时域或者频域检测，容易被ST段其他抬高的病变影响判断。所以，提取一种能反映能量分布以及时频域特征的尺度图(scalogram)组成的特征向量，对于J波的检测是必要的。信号尺度图的定义如下：

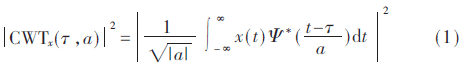
    对QRS波群终点处前8 ms到后40 ms，这48 ms的区域使用连续小波变换。选择尺度范围1～32，母小波选择Morlet小波。为了细化信号的特征，把时间轴划分成9个子区域，把尺度轴划分成12个子区域，这样时间尺度平面被划分成108个区域。计算每个区域的小波系数的平方CWT²(τ，a)，这样就形成了一个108维的特征向量，这个特征向量反映了J波发生区域的能量分布。

    图4是对J波阳性和阴性信号模式QRS波群的终点部分应用连续小波变换，计算出两种信号模式的尺度图。如图4所示，J波阳性和J波阴性模式的小波系数幅值明显不同。整体上看，在图4（b）幅值明显大于图4（a），而且它们的能量分布是不同的。如图5，精细的三维俯视图的研究表明，J波阳性模式和J波阴性模式在能量分布随着时间和尺度的变化有着明显的不同。J波阳性模式的能量集中在整个时间范围内的少数几个尺度上，而J波阴性模式的能量分布相比阳性模式更为分散。因此，基于尺度图特征提取是有效的，它可以作为一个可靠的工具来识别J波阳性和J波阴性。

2.3 识别分类

    从数据集提取特征向量后，提取的5个特征向量整合成一个大特征向量，变成一个综合时频域特征的具有236维的综合特征向量，作为隐马尔科夫分类器的输入。输入向量的维数太大，导致数据冗长，计算量大。因此，需要减少输入向量的维数，而且保持那些对J波敏感的特点。本文选择主成分分析技术进行降维。PCA是一个利用正交线性变换降维的统计学技术^[9]。PCA降维和特征筛选之后，利用隐马尔可夫模型实现J波的自动检测，如图6，其中虚线是隐马尔可夫训练过程，实线是识别过程。

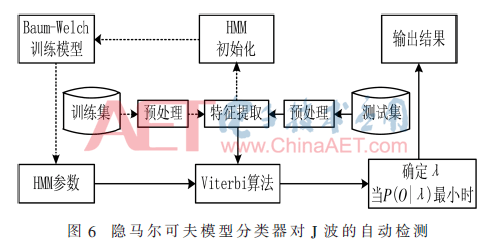
3 实验仿真

    本文选择了4个传统的指标：准确性（ACC）、灵敏度（SE）、特异性（SP）和阳性预测值（PPV）评估J波检测技术的性能。

    从信号处理角度上去识别分类J波信号的研究还处于刚刚起步阶段，现在阶段只有两个团队对J波识别进行过研究。2014年，CLARK E N等学者提出了一个J波的检测方法，该方法是设置了一个QRS波下降支的断点，其数据库是包含从100个平均年龄为24.8±3.2岁的成年男子获得的静息12导联心电图^[10]。2015年，WANG Y G等学者提出了一个J波自动检测方法，该方法利用了信号处理结合功能函数分析技术，取得了89%的敏感性和86%的特异性^[11]。这两种方法的局限性都是数据库范围小，导致实验结果不具有普遍性。为了验证3种方法的有效性，本文验证了3种方法在本文中的构建的大数据库的实验效果，训练集和测试集的分配使用十倍交叉验证的方法。采用十倍交叉验证3种方法的准确性、敏感性、特异性和阳性预测值4个指标的性能如图7～图10所示。

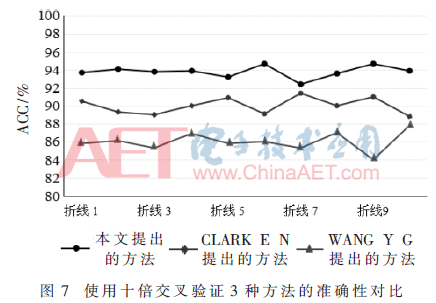
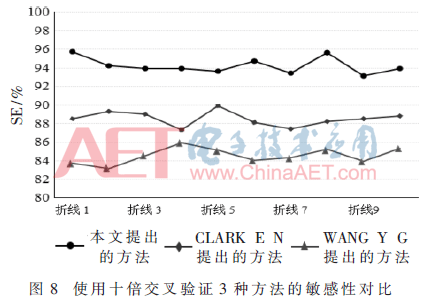
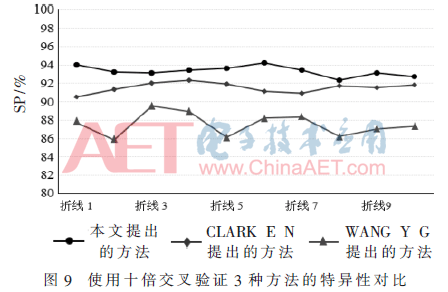
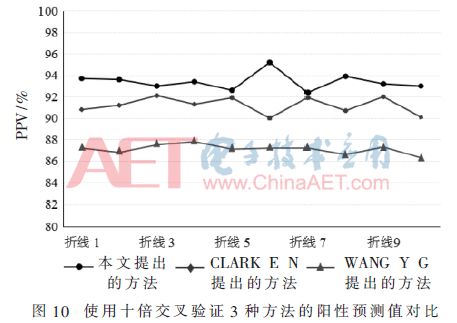
    表1给出了3种自动检测J波的方法的平均性能（准确性、灵敏度、特异性和阳性预测值）。从表中可以得出，本文提出的方法较为理想，性能比较好，提供了93.8%的平均准确率、94.2%的平均敏感性、93.3%平均特异性和93.4%的平均阳性预测值。图11总结了这3种自动检测J波的方法的对比结果。总之，本文提出的方法在心电信号识别系统是有效的，而且具有广阔的开发应用前景。

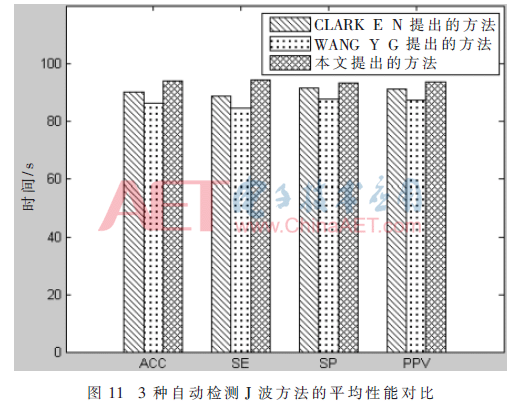
    结果表明，基于本文提出的5种特征向量的J波自动检测技术与其他方法相比，该方法具有较好的分类效果。

4 结论

    本文提出的基于5个特征向量的J波自动识别技术可以综合地反映J波的变异，相比其他方法，该方法具有显著的优势。J波的变异充满了不确定性，其定义有多种标准。这种模糊性使得它很难或不可能从一个角度进行研究。因此，本文提出的J波自动检测方法，可以克服目前研究中诊断J波存在的不一致性，同时本文的自动识别J 波方法对于临床相关病人的诊断和治疗具有十分重要的现实意义。

参考文献

[1] 严干新.异常J波综合征[J].临床心电学杂志，2007，16(1)：3-9.

[2] MARUYAMA M，KOBAYASHI Y，KODANI E，et al.Osborn waves：history and significance[J].Indian Pacing and Electro-physiology Journal，2004，4(1)：33-39.

[3] 崔长琮，严干新.急性缺血性J波和J波综合征的研究现状[J].中华心血管病杂志，2010，38(4)：299-300.

[4] JUNTTILA M J，SAGER S J，TIKKANEN J T.Clinical significance of variants of J-points and J-waves：early repolarization patterns and risk[J].European Heart Journal，2012，33(21)：2639-2645.

[5] CLIFFORD G D，AZUAJE F，MCSHARRY P E.Advanced methods and tools for ECG data analysis[M].Norwood，MA：Artech House，2006.

[6] MAHMOODABADI S Z，AHMADIAN A，ABOLHASANI M D.Feature extraction using daubechies wavelets[C].Proceedings of the Fifth IASTED International Conference on Visualization Imaging and Image Processing，2005：343-348.

[7] THAKOR N V，WEBSTER J G，TOMPKINS W J.Estimation of QRS complex power spectra for design of a QRS filter[J].IEEE Trans.Biomed.Eng.，1984，31(11)：702-706.

[8] YE C，KUMAR B V K V，COIMBRA M T.Heartbeat classification using morphological and dynamic features of ECG signals[J].Biomedical Engineering，IEEE Transactions on，2012，59(10)：2930-2941.

[9] ABDI H，WILLIAMS L J.Principal component analysis[J].Wiley Interdisciplinary Reviews：Computational Statistics，2010，2(4)：433-459.

[10] CLARK E N，KATIBI I，MACFARLANE P W.Automatic detection of end QRS notching or slurring[J].J Electro-cardiol，2014，47(2)：151-154.

[11] WANG Y G，WU H T，DAUBECHIES I，et al.Automated J wave detection from digital 12-lead electrocardiogram[J].Journal of Electrocardiology，2015，48(1)：21-28.