0 引言

    余数系统作为一种数值表征系统，凭借其在并行计算、数字信号处理以及大规模集成电路等领域的潜在应用前景，受到了广泛的研究。近些年来，随着冗余余数系统(Redundant Residue Number System，RRNS)及其相关算法在纠错领域的不断应用，余数基的选择和构建变得愈发重要。模乘单元的性能对于一种基的选择和构建起到了关键的作用，如何提供更多形式的高速模乘法器成为了余数系统发展的关键问题之一。

    2ⁿ-2^p±1形式的基可以构建出高平衡度的余数基，是RRNS中最常用的一种基。其对应的乘法器也已经被广泛的研究。在文献[4]中，一种通用形式的模乘法器被提出，虽然可以用来构造模(2ⁿ-2^p-1)乘法器，但是效果不佳。在文献[5]中，我们提出了一种剩余范围的扩展方法，通过这种方法，在没有开销的情况下将剩余范围从[0，2ⁿ-2^p-1]扩展到[0，2ⁿ-1]，为化简模(2ⁿ-2^p-1)乘法器的结构提供了便利。在文献[6，7]中，基于Booth编码的模(2ⁿ-2^p-1)乘法器被提出，但是由于Booth编码引入了负数，而负数在模乘法器中的修正问题会造成较大的性能损失。文献[8]提出了一种高效且利于EDA实现的TDM压缩树(Three Dimensional Minimization，TDM)算法。考虑到余数系统中乘法器是无符号的且位数不高(通常小于32)，采用非Booth编码的TDM压缩树结构反而可以起到很好的效果。本文提出的模(2ⁿ-2^p-1)乘法器沿用了剩余范围的扩展方法，采用TDM压缩树解决[6，7]中出现的负数修正问题，取得了较大的性能提升。

    本文首先介绍TDM压缩树及剩余范围的扩展方法，然后提出高速模(2ⁿ-2^p-1)乘法器的结构并给出结构图，最后进行分析对比。

1 TDM压缩树算法

    在全加器中，不同输入端到不同输出端的延迟是不同的。文献[8]中提出TDM算法可以将压缩树中不同全加器的最长延迟路径和最短延迟路径相连接。这种算法可以很方便地用脚本实现，具有通用性。为了解决布局布线的不规整的问题，TDM算法支持将全加器替换为4：2或者其他形式的压缩器，以进一步提升速度。最终通过TDM压缩树可以将部分积(Partial Product，PP)压缩至两行。需要注意的是，虽然相较文献[6，7]中采用的Booth编码的混合型压缩结构，TDM压缩树会产生较大的面积，但是考虑到Booth编码引入负数所带来的复杂修正问题，这些面积会被抵消且总的延迟更小。

2 剩余范围的扩展方法

3 高速模(2ⁿ-2^p-1)乘法器的结构

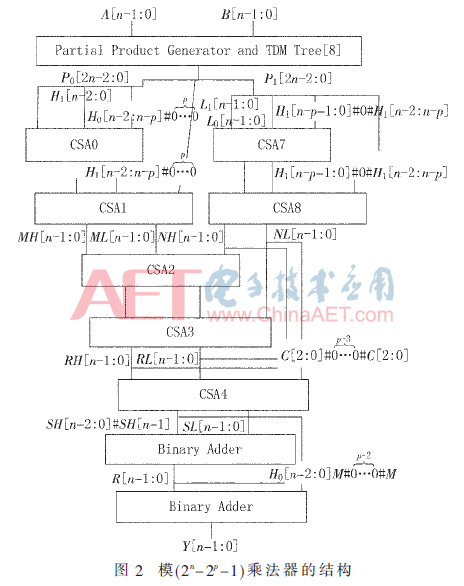
    假设A[n-1:0]是乘数，B[n-1:0]是被乘数，A[n-1:0]×B[n-1:0]所产生的PP被TDM压缩树压缩至两列，分别为P₀[2n-2:0]，P₁[2n-2:0]。模(2ⁿ-2^p-1)乘法器可以被表示为：

    其中H₀[n-2:0]，L₀[n-1:0]分别代表P₀[2n-2:0]的高n-1位和低n位。H₁[n-2:0]，L₁[n-1:0]分别代表P₁[2n-2:0]的高n-1位和低n位。根据文献[5]中模(2ⁿ-2^p-1)乘法器的性质，有：

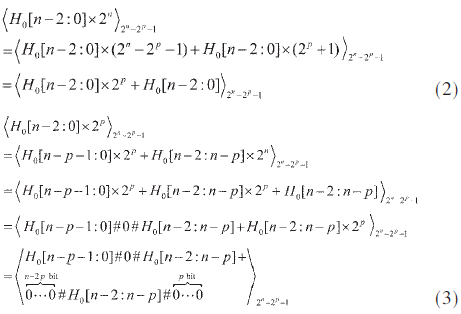
    其中符号#用来连接各比特位。将式(2)、式(3)带入式(1)，可以进一步得到：

    将式(4)中前四项和后四项分别两个(n-1)位的CSA和两个n位的CSA进行处理，可以得到：

其中MH[n-1:0]，ML[n-1:0]为两个(n-1)位的CSA的输出，NH[n:0]，NL[n:0]为两个(n-1)位的CSA的输出。NH[n:0]和NL[n:0]可以进一步折叠：

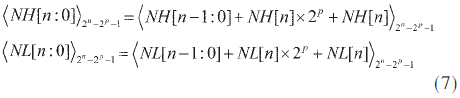
    将四个n位的部分项MH[n-1:0]，ML[n-1:0]，NH[n-1:0]以及ML[n-1:0]继续用两个n位CSA进行处理，得到：

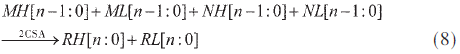
    其中RH[n:0]和RL[n:0]为这两个n位CSA产生的输出且可以继续折叠：

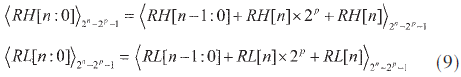
    令C[2:0]=NH[n]+NL[n]+RH[n]+RL[n]，式(9)产生的四个部分项可以进一步用一个n位CSA压缩：

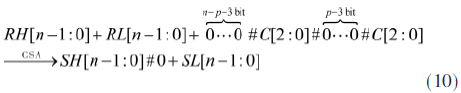
    将得到的SH[n-1:0]修正为：

    将SH[n-2:0]#SH[n-1]和SL[n-1:0]用一个n位二进制加法器相加得到R[n:0]：

其中M=R[n]+SH[n-1]。实验证明当n≥2p时，结果不会溢出。整体结构如图2所示，在关键路径上包含1个TDM压缩树，5个CSA，以及2个n位的二进制加法器。

4 分析与比较

    我们将本文提出的模(2ⁿ-2^p-1)乘法器和文献[4，5，6，7]中的模乘法器进行对比分析。所有的模乘法器都采用Verilog 硬件描述语言进行建模，并采用Design Complier 在90 nm COMS工艺下进行综合。

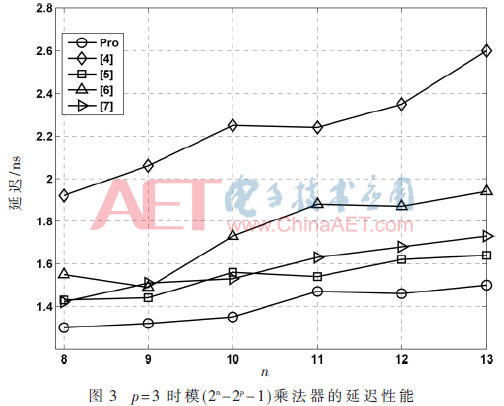
    综合结果表明，相较于文献[4]中的设计，本设计的平均延迟降低49%，平均面积降低了5.1%。与文献[5]中的设计相比，本设计的平均延迟降低了10.4%，但是平均面积提升了4.5%。和文献[6]相比，本设计平均延迟降低了23.2%而平均面积降低了26.1%。与文献[7]进行比较，本设计平均延迟降低了10.3%，平均面积提升了1.3%。

    文献[5，7]中的两种设计是两种典型的高效模(2ⁿ-2^p-1)乘法器，下面将着重对本设计以及文献[5，7]进行静态分析。设计[5，7]都包含一个Booth 编码的压缩树，而本设计包含一个非Booth的TDM压缩树，这两种结构的延迟相差不大。比较重点放在产生两个2n-1位PP后的路径，我们称之为关键路径。文献[5]的关键路径包含1个2n位二进制加法器，1个CSA，3个n位二进制加法器。文献[7]的关键路径包含6个CSA和三个二进制加法器。与文献[5]相比，本设计在关键路径上使用四个CSA替代了一个2n位的大加法器和一个n位的小加法器。与文献[7]相比，本设计在关键路径上减少了一个CSA和一个2n位加法器。采用文献[4]中的单位门评估方法，具体结果如表1所示。

5 结论

    得益于剩余范围的扩展和TDM压缩树的使用，本设计没有使用复杂的模加法器且避免了负数修正问题。相较于当前的模(2ⁿ-2^p-1)乘法器有较大的延迟性能提升，是目前已知的延迟性能最佳的模(2ⁿ-2^p-1)乘法器。

参考文献

[1] 马上，胡剑浩.余数系统在VLSI设计中的基本问题研究与进展[C].中国通信集成电路技术与应用研讨会，2006.

[2] 李磊，胡剑浩，敖思远.高速Booth编码模(2^n—1)乘法器的设计[J].微电子学与计算机，2011，28(11)：191-193.

[3] 胡剑浩，唐青.面向低电压供电数字电路的容错计算系统结构设计[J].电子科技大学学报，2013(6)：831-835.

[4] HIASAT A A.New efficient structure for a modular multiplier for RNS[J].IEEE Transactions on Computers，2000，49(2)：170-174.

[5] LI L，HU J，CHEN Y.An universal architecture for designing modulo(2n-2p-1) multipliers[J].Ieice Electronics Express，2012，9(3)：193-199.

[6] LI L，LI S，YANG P，et al.Booth encoding modulo(2n-2p-1) multipliers[J].Ieice Electronics Express，2014，11(15).

[7] YAN H，LI L，ZHANG Q.A high speed modulo(2n-2p+1) multiplier design[J].Ieice Electronics Express，2015，12(23).

[8] OKLOBDZIJA V G，VILLEGER D，LIU S S.A method for speed optimized partial product reduction and generation of fast parallel multipliers using an algorithmic approach[J].IEEE Transactions on Computers，1996，45(3)：294-306.