0 引言
    目前，在不同终端用户间共享天线的分集技术(即协作通信)，引起了研究者广泛关注。协作通信的概念和模型最早由Sendonaris等人提出[1]，随后Laneman等人在文献[2]中提出了DF(Decode-Forward，译码转发)和AF(Amplify-and-Forward，放大转发)两种典型的协作协议，并分析了两跳系统的中断概率和中断容量。W.Su等在文献[3]中推导出了采用MPSK和QAM调制的DF协作系统的闭式SER精确表达式，同时也提出了一个SER上界以揭示DF协作系统的渐进性能。基于渐进紧的SER近似式，确定了DF协作系统的最优功率分配，然而并未考虑中继位置对SER性能的影响。文献[4]基于以最小化中断概率为目标对最佳中继位置进行了研究。文献[5]基于文献[3]得到的AF协作系统的渐进紧SER近似式，在几种简单的网络拓扑结构中尝试得到最佳中继定位，并对这几种网络拓扑结构的系统性能的优劣性进行了比较。随后文献[6]在文献[5]的基础上研究了多中继系统中的中继位置优化问题。但是，上述文献的研究成果均是在源和中继等功率分配(EPA)的前提下得到的，即并未考虑中继位置对最优功率分配方案的影响。
    文献[7]分析了中继沿椭圆运动时，不同功率分配方案与中继位置对AF协作通信系统SER性能的影响。本文在其基础上，根据单中继DF协作系统的渐进紧SER公式[3]，以最小化SER为目标，研究直线拓扑结构下功率分配和中继位置联合优化问题。
1 系统模型
    单中继两阶段时分协作通信系统的结构框图如图1所示。

图1  单中继三点协作模型

    阶段1：源以广播方式发送信息给中继和目的，发送为功率P₁。源-目的(S-D)接收信号y_sd、源-中继(S-R)接收信号y_sr可表示为：
   

    阶段2：对于DF协作协议，如果中继能够正确译码，则以功率发送译码后的信号，否则中继不发或保持空闲，两阶段总功率保持恒定值，即P₁+P₂=P。此时目的端在阶段2接收到的信号可以建模为^[9]：
   
2 线性拓扑结构模型下的SER性能分析
    本节以平均误码率SER作为系统的性能指标对DF协作通信系统的性能进行分析。

    考虑如图2所示的直线型拓扑结构模型，即中继节点R位于源节点S和目的节点D的连线上。设S到D、S到R、R到D的归一化距离分别为：d_sd、d_sr、d_rd，则有d_sd=1=d_sr+d_rd，dsr、d_rd∈[0，1]。 在直线拓扑结构模型中，忽略阴影衰落效应，只考虑瑞利衰落、路径损耗和加性高斯白噪声对信

3 SER优化分析
    本节将以最小化SER为目标，对功率分配因子λ和中继位置x进行优化分析。
3.1 固定功率分配比下的中继位置优化
    下面讨论在固定的总功率P和功率分配比λ下，中继节点处于何位置时，协作系统的SER最小。
    在这种情况下的最优化问题可以表述为：
   

    求解上式，得到固定功率分配比下的最优中继位置为：
   

    根据式(16)，最优中继位置随功率分配比的变化曲线如图3所示。从图中可以看到：当功率分配方案改变时，最优中继位置也将随之变化。特别地，当λ=0.5，即采用EPA方案时，由式(16)可求得：x=d_sr=0.546 3。

图3  最优中继位置与功率分配比的关系

3.2 固定中继位置下的功率分配比优化
    在某些场景中，中继的位置是固定的，在这种情况下的优化问题可以表述为如下形式：

    根据式(18)，最优功率分配比随中继位置的变化曲线如图4所示。由式(18)和图4可以得到如下两点结论：

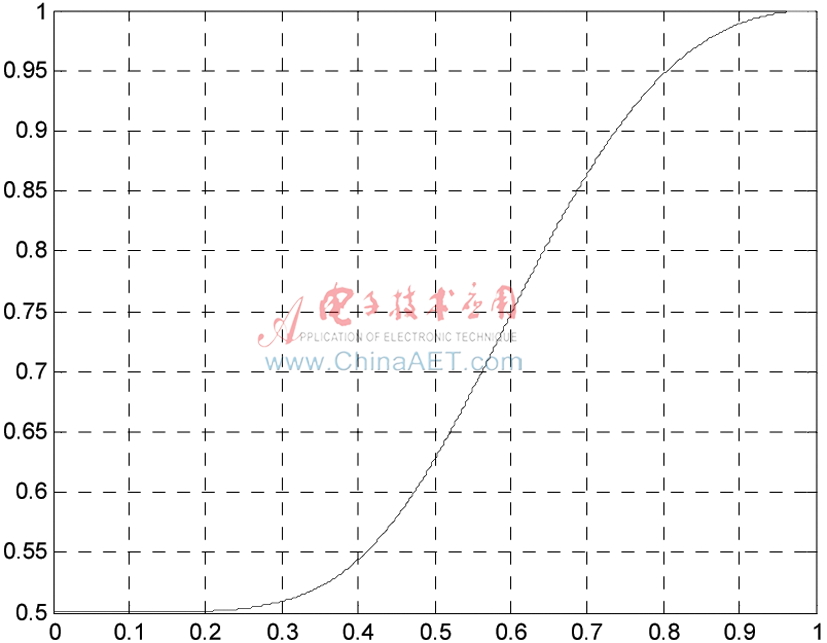
图4  最优功率分配比与中继位置的关系

    (1)最优功率分配与源到目的的信道链路无关，它只依赖源到中继、中继到目的的信道。
    (2)最优功率分配比的取值范围为：0.5≤λ≤1。
    这意味着应该始终把更多的功率分配给源。特别地，当0<x<0.3时，即中继距离源很近时，λ≈0.5，即此时应采用等功率分配(EPA)方案；而当0.9<x<1时，λ≈1，即此时应该将几乎全部功率都分配给源。
3.3 联合优化
    从以上讨论中可以看到最优功率分配比和最优中继位置的范围分别为：0.5≤λ≤1，0≤x≤1。为了得到SER的全局最优值，必须综合考虑功率分配比和中继位置。
    联立式(16)、式(18)得：

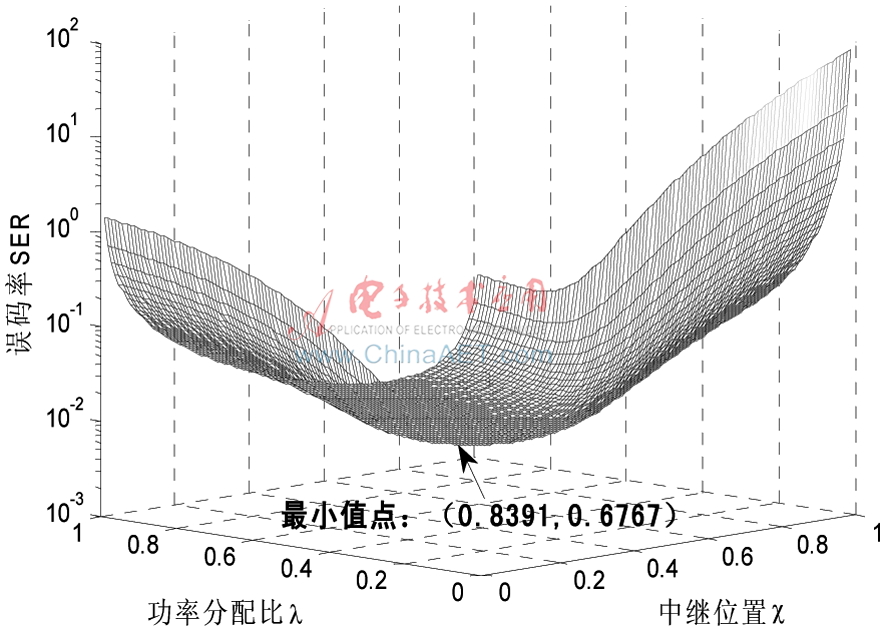
图5  DF协作系统的SER曲面

4 结论
    本文研究了DF协作通信系统的误码率优化问题，推导了线性拓扑结构模型下单中继协作系统的SER表达式，并根据SER表达式，选择合适的功率分配比和中继位置，可以优化系统的SER。最后通过数值分析的方法求解出DF协作系统的最优参数对=(0.839 1，
0.676 7)。值得注意的是，当采用M-PSK调制的DF协作系统的调制星座一定时，此优化参数对的数值便是固定的，与系统总功率等其他因素无关，这可以为DF协作系统的设计提供一个参考依据，例如，在单中继线性拓扑网络中，若分布有多个中继节点，优先选择最接近归一化距离为X**的节点作为源的中继伙伴，同时基站的功率分配比设定为λ**，这样便可以获得最优的SER性能。
参考文献
[1] ERKIP S E，AAZHANG B.User cooperation diversity-part I：system description[J].IEEE Trans.Communication，2003，51(11)：1927-1938.
[2] LANEMAN J N，TSE D N C，WORNELL G W.Cooperative diversity in wireless networks：efficient protocols and outage behavior[J].IEEE Trans.Information  Theory，2004，50(12)：3062-3080.
[3] SU W，SADEK A K，LIU R J K.SER performance analysis and optimum power allocation for decode-and-forward cooperation protocol in wireless networks[C].In Proc.IEEE WCNC，2005，2：984-989.
[4] MENG Y，JING L，SADIADPOUR H.Amplify-forward and decode-forward：the impact of location and capacity contour[C].Military Communications Conference，2005，11(3)：1609-1615.
[5] Xu Lei，Zhang Hongwei，Li Xiaohui，et al.Optimum relay location in cooperative communication networks with single AF relay[J].Communications，Network and System Sciences，2011，4：147-151.
[6] GURRALA K K，DAS S.Impact of relay location on the performance of multi-relay cooperative communication[C].IJCNWC，2012，2(2)：2250-3501.
[7] LIN F，LI Q H，LUO T，et al.Impact of relay location according to SER for amplify-and-forward cooperative communications[C].2007 IEEE International Workshop on
Anti-counterfeiting, Security，Identification.Xiamen，2007，4.
[8] XUE K，HONG X，CHEN L，et al.Performance analysis and resource allocation of heterogeneous cognitive gaussian relay channels[C].Global Communications Conference (GLOBECOM)，2013 IEEE，2013：1167-1172.
[9] TERA A D，GURRALA K K，DAS S.Power allocation for AF cooperative relaying using particle swarm optimization[C].In Green Computing Communication and Electrical Engineering(ICGCCEE)，2014 International Conference on.IEEE，2014，3.