文献标识码: A
DOI:10.16157/j.issn.0258-7998.2015.11.025
中文引用格式: 梁溪,龙翔林,章恩友,等. 基于竞争机制的LDPC码串行最小和算法[J].电子技术应用,2015,41(11):89-92,100.
英文引用格式: Liang Xi,Long Xianglin,Zhang Enyou,et al. A serial min-sum algorithm for LDPC codes based on competitive scheme[J].Application of Electronic Technique,2015,41(11):89-92,100.
0 引言
随着信息化的发展,人们对低密度奇偶校验(Low Density Parity Check,LDPC)码有了重新的认识。LDPC码作为高效的信道纠错编码,具有较低的译码复杂度,系统吞吐量较大,已在电力线载波(Power Line Carrier,PLC)通信、第三代和第四代无线移动通信等方面得到了广泛应用[1]。相对于turbo译码算法[2],采用LDPC编码和置信传播(Belief Propagation,BP)译码算法更受人们的青睐[3]。但是BP算法存在对硬件存储量的需求较大以及对信道情况较为敏感等问题。人们更趋向于鲁棒性更好和复杂度更低的译码算法,最典型的就是并行最小和(Parallel Min-Sum,PMS)算法[4]。这类算法在实现中只需要加法和比较运算,且不需要知道信道情况,可以获得性能和复杂度的良好折衷。考虑到PMS算法前后两次迭代译码过程中,参与信息交换的置信度被过高估计,文献[5]通过引入归一化权重因子来减少这种负面影响,使其性能逼近最优BP算法的性能,可称之为归一化并行最小和(Normalized Parallel Min-Sum,N-PMS)算法。随着研究的深入,人们提出了不同的译码机制来提高置信传播的效率,其中较为重要的一类是采用权重因子的串行最小和(Normalized Serial Min-Sum,N-SMS)算法[6]。在电力线载波通信中,收发模块通常采用具有低存储量和低复杂度的编、译码算法。N-SMS算法虽然在存储上较N-PMS算法有一定减少,但N-SMS算法由于每次迭代都采用min操作来更新最小值,复杂度相对较高。
为实现可靠通信,并综合考虑实现成本、器件功耗以及处理复杂度的问题,针对N-SMS算法提出了一种基于竞争机制的归一化的串行最小和(Normalized Competitive Min-Sum,N-CMS)算法。该算法在按照自然顺序更新变量节点对校验节点消息的同时,还利用竞争关系更新变量节点对校验节点消息集合中的最小值。与文献[6]类似的是,N-CMS在更新某一变量节点时,同时利用了与该节点之前已更新的软信息和该节点之后还未更新的软信息,所以N-SMS算法与N-CMS算法的性能相同。不同的是,N-CMS通过采用竞争机制来更新属于同一校验式的变量节点集合中的最小值,避免了文献[6]中采用min操作的复杂运算,并进一步减少了存储量。
1 N-PMS算法简介
为了简化叙述,该文沿用文献[7]中的部分符号定义。设m和n分别表示校验节点和变量节点,H为LDPC码对应的校验矩阵,当变量节点和校验节点有边相连接时,则hmn=1,它是H中的第m行和n列的元素。N(m)={n|hmn=1}表示参与校验方程m的变量节点的集合,N(m)\n为N(m)中除去元素n后构成的集合;相应地,M(n)={m|hmn=1}表示与变量节点n相连的校验节点的集合,M(n)\m为集合M(n)中除去元素m后构成的集合。设![26)IPLI]CR2JI[@1M7JC_S4.png 26)IPLI]CR2JI[@1M7JC_S4.png](http://files.chinaaet.com/images/2017/01/12/6361982660851053851171961.png) 是从变量节点n传递给校验节点m的软信息,表示在给定接收序列y,并且除了第m个校验方程外,其他与n相关的校验方程都满足的条件下,xn=x的概率;
是从变量节点n传递给校验节点m的软信息,表示在给定接收序列y,并且除了第m个校验方程外,其他与n相关的校验方程都满足的条件下,xn=x的概率;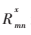 是由校验节点m传递给变量节点n的软信息,表示在xn=x,且参加第m个校验方程的除n外的其他变量节点
是由校验节点m传递给变量节点n的软信息,表示在xn=x,且参加第m个校验方程的除n外的其他变量节点 的概率Qmn已知的条件下,该校验方程成立的概率,其中
的概率Qmn已知的条件下,该校验方程成立的概率,其中 ∈N(m)\n。
∈N(m)\n。
设s为长为N的编码序列x=[x1,x2,…,xN]T经过BPSK调制后的信号,g是均值为0、方差为![HV[]OZ%0X@XAT0M4Z3UB6JF.png HV[]OZ%0X@XAT0M4Z3UB6JF.png](http://files.chinaaet.com/images/2017/01/12/6361982673620953857988851.png) 的高斯噪声。设s经过AWGN信道后的接收序列为y=[y1,y2,…,yN]T,BP译码后的序列为
的高斯噪声。设s经过AWGN信道后的接收序列为y=[y1,y2,…,yN]T,BP译码后的序列为![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982674820453851559832.png) 。其中
。其中
![1S9Q8U5@KC4{JR9]APHB]~Y.png 1S9Q8U5@KC4{JR9]APHB]~Y.png](http://files.chinaaet.com/images/2017/01/12/6361982675601153858367176.png)
传统的N-PMS算法可归纳如下:
初始化:令先验信息L(Pn)=yn,L(Qnm)=L(Pn)
步骤1:判断是否达到设定的最大迭代次数MT,若是则程序结束;否则执行步骤(2)。
步骤2:对m=1,2,…,M和所有的n∈N(m)计算:
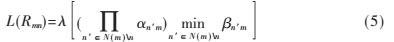
在上式中,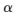 nm=sign(L(Qnm))和
nm=sign(L(Qnm))和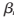 nm=abs(L(Qnm)),分别表示L(Qnm)的符号和绝对值,
nm=abs(L(Qnm)),分别表示L(Qnm)的符号和绝对值,![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982682270853854838095.png) 为归一化权重因子,满足0≤
为归一化权重因子,满足0≤![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982682682553855976389.png) ≤1。
≤1。
步骤3:对n=1,2,…,N和所有的m∈M(n)计算:
![Y9S55%}ZS88)OMZSI3]KQ%S.png Y9S55%}ZS88)OMZSI3]KQ%S.png](http://files.chinaaet.com/images/2017/01/12/6361982683921053859485236.png)
L(Qnm)=L(Qn)-L(Rmn)(7)
步骤4:对译码软信息进行硬判决,若L(Qn)<0,则![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982685632453859623498.png) n=1,否则
n=1,否则![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982686473053854788240.png) n=0,n=1,2,…,N。若H
n=0,n=1,2,…,N。若H![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982688874153854208334.png) T=0,则译码成功,程序结束,否则转到步骤(1)。
T=0,则译码成功,程序结束,否则转到步骤(1)。
2 N-CMS算法的原理与实现步骤
在N-PMS中,校验节点和变量节点是分别并行更新的。文献[4]指出,对于H矩阵中的第m个校验式,N-PMS在计算所有n∈N(m)集合中的最小值![M]B7]J{]Q5N72MRH8~~%0S4.png M]B7]J{]Q5N72MRH8~~%0S4.png](http://files.chinaaet.com/images/2017/01/12/6361982691770453852993720.png) 时,可以通过找出该集合中最小的两个量
时,可以通过找出该集合中最小的两个量![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982693506853851373096.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982693910653853015824.png) 2来简化运算。
2来简化运算。
基于文献[4]的思想,设变量节点n更新前与更新后L(Qnm)的绝对值分别为 nm和
nm和![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982702455653856858088.png) ,
,![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982694377753853276462.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982695011253857577285.png) 2是集合n∈N(m)所有
2是集合n∈N(m)所有 nm中最小的两个值,不失一般性令
nm中最小的两个值,不失一般性令![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982695474553855928048.png) 1≤
1≤![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982695854853859849578.png) 2。当
2。当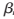 nm完成到
nm完成到![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982705695753857052079.png) 的更新后,使得n∈N(m)集合在
的更新后,使得n∈N(m)集合在 nm更新前求得的
nm更新前求得的![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982707412453857277207.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982707844253854185641.png) 2可能并不是当前最小的两个值,例如存在?茁
2可能并不是当前最小的两个值,例如存在?茁![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982708633953857494379.png) <
<![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982708985253858398543.png) 1的情况,此时的两个最小值应为
1的情况,此时的两个最小值应为![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982709755953858814577.png) 和
和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982710281253859948245.png) 1。倘若不对
1。倘若不对![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982757252053852353500.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982757714653853653131.png) 2进行更新,则会导致
2进行更新,则会导致![M]B7]J{]Q5N72MRH8~~%0S4.png M]B7]J{]Q5N72MRH8~~%0S4.png](http://files.chinaaet.com/images/2017/01/12/6361982711444753851738792.png) 的值不准确,使得性能和收敛速率都会受到影响。但若要采用min操作来更新
的值不准确,使得性能和收敛速率都会受到影响。但若要采用min操作来更新![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982715903753857029017.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982716531153856476624.png) 2,则计算复杂度会较高。如在文献[6]中,对于码率1/2的规则(N,J,2J)LDPC码,N-SMS在每次迭代中,
2,则计算复杂度会较高。如在文献[6]中,对于码率1/2的规则(N,J,2J)LDPC码,N-SMS在每次迭代中,![M]B7]J{]Q5N72MRH8~~%0S4.png M]B7]J{]Q5N72MRH8~~%0S4.png](http://files.chinaaet.com/images/2017/01/12/6361982713952853855977299.png) 操作需要NJ(2J+「log22J-2)次加法运算,当J较大时,简化N-SMS算法的复杂度是很有必要的。
操作需要NJ(2J+「log22J-2)次加法运算,当J较大时,简化N-SMS算法的复杂度是很有必要的。
![E@B({A)8__9C65S6]01U%1E.png E@B({A)8__9C65S6]01U%1E.png](http://files.chinaaet.com/images/2017/01/12/6361982718622553855419686.png)
步骤1:判断是否达到设定的最大迭代次数MT,若是则程序结束;否则按照n=1,2,…,N的顺序更新变量节点对校验节点的消息,执行步骤(2)。
步骤2:对特定的n和每一个m∈M(n)按照式(5)计算L(Rmn),此处的min操作由![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982769948753854273565.png) 1和
1和![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982770489553854150520.png) 2取代。
2取代。
步骤3:对特定的n和每一个m∈M(n)依据式(6)、式(7)算出L(Qn)和L(Qnm),由更新后的L(Qnm)得出![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982721736653853948716.png) 后,再根据竞争模式更新
后,再根据竞争模式更新![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982751840953855939381.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982752294753855699016.png) 2。
2。
步骤4:若n≤N,对译码软信息进行硬判决,若L(Qn)<0,则![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982723247653856843823.png) n=1,反之
n=1,反之![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982723779153857636772.png) n=0,n=n+1转到步骤(2)。否则执行步骤(5)。
n=0,n=n+1转到步骤(2)。否则执行步骤(5)。
步骤5:若H![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982724433853854422065.png) T=0,则译码成功,程序结束。否则转到步骤(1)。
T=0,则译码成功,程序结束。否则转到步骤(1)。
3 复杂度及存储量分析


另一方面,N-PMS需要较大的存储,根据式(5),对于每个校验式m,![M]B7]J{]Q5N72MRH8~~%0S4.png M]B7]J{]Q5N72MRH8~~%0S4.png](http://files.chinaaet.com/images/2017/01/12/6361982728930653857322904.png) 需要2个单元来存储2个最小值,所以对于N/2个校验式,L(Rmn)总共需N个存储单元;根据式(6)、式(7),L(Qn)、L(Qnm)分别需N和NJ个存储单元。再来看N-SMS算法,由于变量节点串行更新,L(Rmn)只需2J个存储,但N-SMS算法每次迭代都要进行min操作,对于每个校验式m,L(Qnm)仍需2J个
需要2个单元来存储2个最小值,所以对于N/2个校验式,L(Rmn)总共需N个存储单元;根据式(6)、式(7),L(Qn)、L(Qnm)分别需N和NJ个存储单元。再来看N-SMS算法,由于变量节点串行更新,L(Rmn)只需2J个存储,但N-SMS算法每次迭代都要进行min操作,对于每个校验式m,L(Qnm)仍需2J个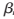 nm来计算
nm来计算![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982730581953854822252.png) ,从而L(Qn)、L(Qnm)分别仍需N和NJ个存储单元。在N-CMS算法中,L(Rmn)也只需2J个存储,由于N-CMS算法采用了竞争机制,每计算出一个
,从而L(Qn)、L(Qnm)分别仍需N和NJ个存储单元。在N-CMS算法中,L(Rmn)也只需2J个存储,由于N-CMS算法采用了竞争机制,每计算出一个![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982731943953858768767.png) ,便用于
,便用于![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982754883153854473189.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982755314553859933187.png) 2的更新。所以对于每个校验式m,只需分配1个临时单元用于存储
2的更新。所以对于每个校验式m,只需分配1个临时单元用于存储![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982732377553858884232.png) ,从而L(Qnm)共需N/2个单元,L(Qn)需N个存储单元。综上所述,N-PMS、N-SMS和N-CMS所需存储总量分别为2N+NJ、N+(N+2)J和3N/2+2J。显而易见,相对于N-PMS算法和N-SMS算法,N-CMS算法具有极低的存储需求,这对于设计成本低廉的译码模块具有重要意义。
,从而L(Qnm)共需N/2个单元,L(Qn)需N个存储单元。综上所述,N-PMS、N-SMS和N-CMS所需存储总量分别为2N+NJ、N+(N+2)J和3N/2+2J。显而易见,相对于N-PMS算法和N-SMS算法,N-CMS算法具有极低的存储需求,这对于设计成本低廉的译码模块具有重要意义。
4 算法仿真与测试
仿真中选取码率1/2的(512,3,6)规则LDPC码通过AWGN信道,译码分别采用N-PMS算法和N-CMS算法。为了使得信息得到充分的传播,在仿真中令最大迭代译码次数MT=30。下面从归一化权重因子的选取、误比特率(Bit Error Rate,BER)、误帧率(Frame Error Rate,FER)、收敛速率和译码平均译码复杂度几个方面来进行对比分析。
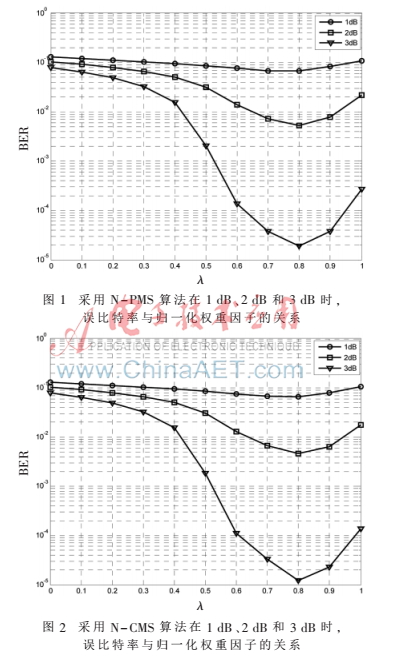
为简化讨论,此处利用蒙特卡罗方法来获得N-PMS和N-CMS的归一化权重因子。如图1和图2所示,两者都在![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982737670953854738452.png) =0.8时表现出最佳的性能,因此将
=0.8时表现出最佳的性能,因此将![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982738001053857096666.png) =0.8作为最佳归一化权重因子用于之后的仿真。
=0.8作为最佳归一化权重因子用于之后的仿真。

图3和图4分别对比了PMS、N-PMS、CMS和N-CMS系统的BER和FER性能,按照是否引入归一化权重因子分为两组,即PMS和N-PMS,CMS和N-CMS。可以看出,不论哪一组归一化算法均比非归一化的算法性能要好得多,约有0.5~0.7 dB的性能差距。此外,即使都是归一化算法,N-CMS较N-PMS也有0.1~0.2 dB的性能提升。


由图5可知,CMS所需的平均迭代译码次数要少于PMS,类似的,N-CMS所需的平均迭代译码次数也少于N-PMS。从图6可以得出,N-CMS在中低信噪比时译码复杂度较N-SMS有明显的优势,但比N-PMS略高;在高信噪比时N-CMS与N-PMS复杂度接近,而且两者都比N-SMS的复杂度低。
5 结论
本文提出了一种按照变量节点更新的归一化串行最小和算法——N-CMS。N-CMS算法采用竞争机制实时更新变量节点对校验节点消息集合中最小的两个值,它在保持与N-SMS算法相同性能的前提下大幅降低了运算量。相对N-PMS算法而言,N-CMS算法不论是在收敛速度,还是在译码性能上都更有优势,其复杂度只有略微增加。最为重要的是N-CMS算法具有极低的存储需求,尤其是在电力线载波通信所需的译码模块的设计中,表现出巨大的实用价值。
参考文献
[1] DEVELI I,KABALCI Y.Analysis of the use of different decoding schemes in LDPC coded OFDM systems over indoor PLC channel[J].Electronics & Electrical Engineering,2014,20(1):76-80.
[2] BERROU C,GLAVIEUX A,THITIMAJSHIMA P.Near Shannonlimit error-correcting coding:turbo codes[C].In ICC93,1993(5):1064-1070.
[3] MACKAY D J C.Good error-correcting codes based on very sparse matrice[J].IEEETrans.Inform.Theory,1999(45):399-431.
[4] FOSSORIER M P C,MIHALJEVIC M,IMAI H.Reduced complexity iterative decoding of low density parity check codes based on belief propagation[J].IEEE Trans.Commun,1999(47):673-680.
[5] CHEN J,FOSSORIER M P C.Decoding low-density parity check codes with normalized APP-based algorithm[C].Proc.IEEE Global Communications Conference,2001,9(1):1026-1030.
[6] 刘原华,王新梅,胡树楷,等.一种改进的卷积LDPC码置信传播译码算法[J].西安电子科技大学学报,2009, 36(3):424-428.
[7] 杨帆,罗振东,田宝玉.改进的LDPC串行译码[J].北京邮电大学学报,2008,31(4):130-134.

