文献标识码: A
DOI:10.16157/j.issn.0258-7998.2016.12.025
中文引用格式: 张金玲,潘绯,张争光,等. 时变OFDM系统中基于基扩展模型的物理层认证[J].电子技术应用,2016,42(12):97-99.
英文引用格式: Zhang Jinling,Pan Fei,Zhang Zhengguang,et al. Physical-layer authentication based on basis expansion model in time-variant OFDM systems[J].Application of Electronic Technique,2016,42(12):97-99.
0 引言
基于信道信息的物理层认证利用了丰富的无线信道资源,以信道为“指纹”特征,是一种对传统认证技术的有效补充和增强[1,2],但是物理层认证在时变情况下受到挑战。本文讨论时变信道中连续数据帧的认证,当前后两个数据帧的时间间隔小于信道的“相干时间”,同时非法攻击者与合法发送者之间的距离大于传输波长的一半的情形下进行。传统的结合最小二乘(Least Square,LS)和二元假设检验的物理层认证利用了无线信道响应的时空唯一性[3],但是由于利用LS方法进行信道探测时不考虑可分径的各个抽样值的相关性,无法准确跟踪时变信道的时变特性。本文提出采用基扩展模型(Basis Expansion Model,BEM)作为信道探测的方法,其特点在于将可分径的各个抽样值在块传输时间内存在相关性作为一种资源,用于补充和增强移动通信的接入安全认证机制。
1 系统模型
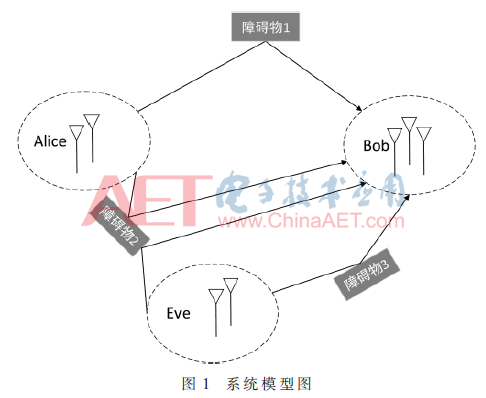
本文的认证涉及到3种不同的身份,分别是:合法发送者Alice、合法接收者Bob,以及企图伪冒Alice来欺骗Bob的非法发送者Eve。如图1所示,Alice和Eve发送的信号经历不同的路径到达接收端Bob处,Bob通过物理层认证区分这些不同,从而判断消息是否合法。
在OFDM系统中,OFDM符号是传输的基本单元。本文信道建模也是在一个OFDM符号中展开的,设信道多径数为L,子载波数为N。BEM模型拟合时变信道,实质上是拟合时域信道的冲击响应。第l个信道抽头在n时刻的信道冲击响应为h(n,l),BEM模型采用相互正交的基函数和不变的基系数来逼近该状态[4],表示为:
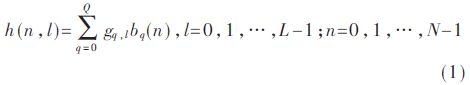
式中:Q为BEM模型的阶数;gq,l为第l个信道抽头的第q个基系数,保持不变;bq(n)为第q个基函数,不同的BEM模型产生不同的基函数。
1.1 复指数BEM模型
复指数基扩展模型(Complex Exponential BEM,CE-BEM)是最常见的模型,采用傅里叶基作为基函数,即:

其中,ωq=2π(q-Q/2)/N。采用Q阶复指数BEM模型对信道建模时,采用了多普勒谱的Q+1个分量,误差较大,容易导致频谱泄露,引起吉布斯效应。文献[5]将其改进为过采样CE-BE(Oversampling CE-BEM,OCE-BEM)将周期设为CE-BEM的p倍,避免频谱泄露现象。
1.2 多项式BEM模型
多项式BEM模型(Polynomial BEM,P-BEM)采用泰勒级数展开得到的多项式的线性组合来拟合信道,基函数为:

P-BEM对多普勒扩展敏感,仅适用于低多普勒扩展的情况。
1.3 离散卡-洛BEM模型
离散卡-洛BEM模型(Discrete Karhunen-Loeve BEM,DKL-BEM)在均方误差准则下最优。但是,适用DKL-BEM的前提是必须已知信道的相关矩阵,并且信道的多功率谱满足特定的形状。
1.4 离散长椭球序列BEM模型
离散长椭球序列BEM模型(Discrete Prolate Spheroidal BEM,DPS-BEM)适用于所有的信道类型。它采用矩形功率谱构成阶方阵,再经计算得到基函数。
1.5 基模型选取
经以上分析,CE-BEM模型误差大,容易导致频谱泄露;P-BEM模型对多普勒扩展敏感;DKL-BEM模型必须已知信道的相关矩阵,并且要求信道的多功率谱满足特定的形状,实际认证中无法满足该条件;DPS-BEM模型计算较为复杂。本文中考虑可行性和高效性,选取OCE-BEM模型来拟合无线认证环境中的时变信道。
2 二元假设检验统计量
时变信道中,在满足物理层认证条件的前提下,Bob对发送的连续消息可以通过二元假设检验[6]来实现认证。

当“差值”小于“阈值”时,信道矩阵很相似,判定当前发送者为Alice;当“差值”大于“阈值”时,信道矩阵不相似,判定当前发送者为Eve。由此可见,“差值”的计算和“阈值”的选取是物理层认证的关键。
2.1 改进的归一化LRT方法
计算“差值”需要先选定检验统计量,信道响应的幅度差和相位差是最常用的检验统计量。由于基于幅度的检验统计量和基于幅度和相位的统计检验量均含有未知的噪声功率σ2,无法直接计算“绝对差值”。改进的归一化似然比检验(Likelihood Ratio Test,LRT)方法使用连续3个数据帧(前两帧已认证,第3帧待认证),求“相对差值”,消除了噪声功率σ2。改进的归一化LRT统计量为:
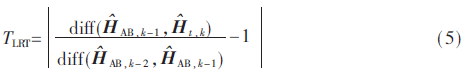
2.2 基于幅度的改进的归一化LRT统计量
基于幅度的改进归一化LRT统计量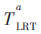 考虑信道响应的幅度差,可得:
考虑信道响应的幅度差,可得:
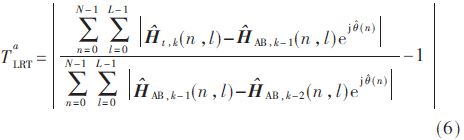
2.3 基于幅度和相位的改进归一化LRT统计量
基于幅度和相位的改进归一化LRT统计量考虑信道响应的幅度差和相位差,可得:
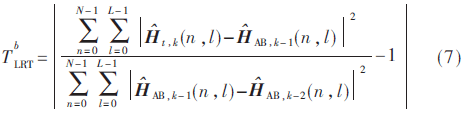
3 仿真实验
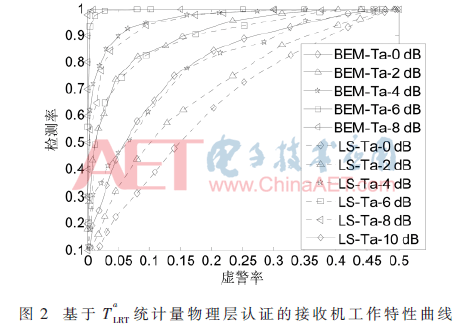
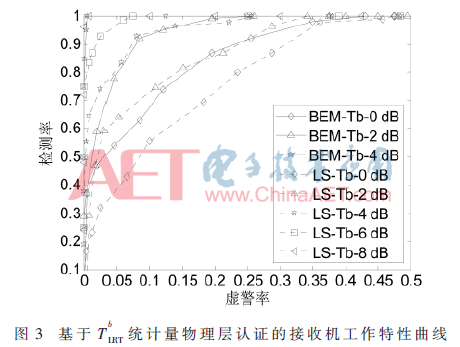
本文采用Jakes模型产生瑞利信道,信道多径数为6,采样间隔为5 μs,子载波数为256,循环前缀长度为30,载波频率为2 GHz,智能终端速度为40 km/h。基于BEM信道估计的导频开销为7/32(一个导频簇长度为7),基于LS信道估计的导频开销为1/4(导频间隔为3),近似认为二者导频开销相等。设定BEM和LS信道估计的其他仿真条件均相同,分别在基于 统计量情况下,“阈值”选取(0,3),仿真1 000次。图2和图3分别为基于
统计量情况下,“阈值”选取(0,3),仿真1 000次。图2和图3分别为基于 统计量的物理层认证中接收机Bob的工作特性曲线。
统计量的物理层认证中接收机Bob的工作特性曲线。

4 结论
本文提出基于基扩展模型的物理层认证方法,通过在OFDM系统中进行的仿真实验,证明该认证方法的有效性,且相对于传统的LS信道探测的物理层认证,获得2~4 dB性能提升。性能提升的原因主要是信道探测准确率提高,原因有二:(1)基于BEM信道估计的导频簇中两侧为保护导频,降低了时变子载波间干扰的影响,非零导频处的信道估计准确率更高;(2)基于BEM信道估计考虑了各个抽样值在块传输时间内存在相关性,比“插值”更准确地跟踪信道变化,从而使数据处信道估计准确度高。
参考文献
[1] XIAO L,GREENSTEIN L,MANDAYAM N,et al.Finger-prints in the ether:Using the physical layer for wireless authentication[C].IEEE International Conference on Communications(ICC′07),2007:4646-4651.
[2] WEN H,WANG Y,ZHU X,et al.Physical layer assist authentication technique for smart meter system[J].IET Communications,2013,7(3):189-197.
[3] MA T,JIANG Y,WEN H,et al.Physical layer assist mutual authentication scheme for smart meter system[C].IEEE Conference on Communications and Network Security(CNS 2014),2014:494-495.
[4] 李昕.基于基扩展快时变信道模型的OFDM系统信道估计[D].成都:西南交通大学,2013.
[5] LEUS G.On the estimation of rapidly time varying channels[C].EUSIPCO 2004,Vienna,Austria,2004:2227-2230.
[6] 胡细宝,孙洪祥,王丽霞.概率论·数理统计·随机过程[M].北京:北京邮电大学出版社,2007.
[7] 马婷.智能电网中的轻量级物理层辅助认证技术研究[D].成都:电子科技大学,2015.

