张志禹，孙戈，徐高晨，许耀斌

　　（西安理工大学 自动化与信息工程学院陕西 西安 710048）

       摘要：传统抛物线方程方法求解起伏地形路径下的电波传播无法反映反射和散射效应，对刃峰地形、类似高斯型地形等起伏地形，采用分步傅里叶变换方法求解双向抛物线方程方法并考虑前向和后向传播的叠加总场，将计算结果与传统抛物线方程方法进行比较，预测结果更准确。

　　关键词：电波传播；双向抛物线方程；分步傅里叶变换方法

　　中图分类号：TN011文献标识码：ADOI： 10.19358/j.issn.1674-7720.2016.24.025

　　引用格式：张志禹，孙戈，徐高晨，等. 基于宽角双向抛物线方程的高频电波传播预测方法［J］.微型机与应用，2016,35（24）：87-90.

0引言

　　抛物线方程（Parabolic Equation, PE）模型是在研究电波在光滑地表绕射传播特性时提出的［1］，其理论依据是在一定条件下对二阶椭圆型的波动方程进行因式分解，取其传播方向上一阶导数的抛物型方程。目前PE模型求解方法主要分为三类：DMT法［2］、FD法［3］、有限元法［4］。由于障碍物的遮挡是影响电波传播的重要因素，对于前向传播的PE模型，并没有考虑电波传播遇到障碍物时的反射效应，会给预测带来一定的偏差。文献［5］利用双向PE模型反演对障碍物进行定位，取得了很好的效果。本文利用双向PE模型分别预测单个起伏地形和多个起伏地形环境下的高频电波传播特性，将数值计算结果与单向PE模型比较，验证了双向PE模型具有更准确的预测结果。

1宽角双向抛物线方程模型

　　1.1双向抛物线方程模型

　　双向抛物线方程模型在传统PE模型基础上考虑后向传播，将后向传播场按距离步进叠加到前向传播场，从而获得整个观测区域的电波传播场分布。当电波传播遇到起伏地形时，使用地形平移模型。地形平移法是对地形屏蔽法的改进，该方法不需要近似处理地形，只需要计算每一步迭代时的地形高度差，再根据地形高度差确定垂直方向平移的计算区域场值点数，平移方向根据地形斜率判断。

　　在直角坐标系(x,y,z)下，x表示距离，z表示高度。假设ψ与y无关，则从Maxwell方程组推导的波动方程满足下式：

　　

　　式（2）中第一式表示前向传播即为传统PE模型，第二式表示后向传播。由于Q计算比较复杂，FeitFleck近似法可将伪微分算子Q展开为：

　　式中p=ksinθ，表示z的Fourier变换域，θ为电波到水平方向的角度。

　　对伪微分算子Q用FeitFleck近似法，考虑前向和后向传播，则有：

　　

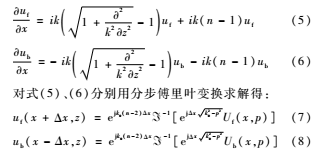
　　式中uf、ub分别表示前向、后向传播的空间域，Uf、Ub分别表示前向、后向传播的P域场值，ub反映传播电波遇到障碍物时的反射效应。

　　1.2单双刃峰原理

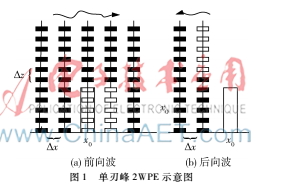
　　以单刃峰环境为例，单刃峰位于发射点水平距离xobs处，高为hobs，2WPE算法示意图如图1所示，电波从初始场x=0处沿x轴向右传播，在传播中遇到障碍物时发生反射效应，因此电波达到刃峰之前只考虑前向传播，到达刃峰时分解为前向传播和后向传播两个分量，两者分别沿x轴的正方向和负方向。通过边界条件得到刃峰处后向传播的初始场如式（9）：

　　图1单刃峰2WPE示意图

　　整个计算区域的总场可以表示为：

　　由式(10)看出：电波传播在单刃峰路径上时，电波在刃峰处被分解，具有电磁波的绕射和反射效应。当前向传播到达计算区域最大处时，后向传播到达天线发射处，整个计算才结束。

　　当障碍物为多刃峰时，由于反射作用，在两个刃峰之间会出现无穷多项前向传播和后向传播，因此计算时，要进行反复迭代，图2为双刃峰2WPE算法示意图。

2数值算例

　　下面具体分析单个起伏地形和多个起伏地形环境下，2WPE模型预测电波传播特性，并将其结果与单向PE模型比较。在以下算例中假设频率都为1 000 MHz，电磁波水平极化，天线方向图为高斯型，波束宽度为3°，水平地面和起伏地形均为理想导体。

　　2.1类似高斯型地形对电波传播的影响

　　地形函数为：

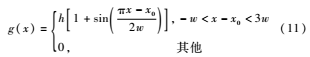
　　其中x0为包络半高程到天线发射点的距离，w为包络半宽度，h为高斯包络的垂直高度。

　　取x0=24 km，w=1.25 km，h=500 m。

　　图3为传统PE模型和2WPE模型的传播因子分布剖面图，传播因子单位按分贝（dB）计算。从图中可以看出，传统的PE模型只能计算前向传播，而2WPE模型能同时计算前向和后向传播。观测点位于障碍物左侧区域时，传统PE模型结果偏差较大；观测点在障碍物右侧区域时，两种模型计算的结果一致。

　　下面具体分析两种模型的传播特性，图4给出传播因子随水平距离的变化曲线，两个图中观察点的垂直高度分别为600 m和400 m。综合分析图3(a)和图3(b)，高斯地形左侧0~20 km区域内，传统PE模型由于本身算法限制而无法计算后向传播，因此传播因子非常小，而2WPE模型叠加了反射波，预测结果更加精确。两个图中的障碍物左侧区域，2WPE模型得到的传播因子曲线出现波动，这是前向传播与后向传播叠加的结果；在x=25 km后，两种模型都只有前向传播，因此曲线基本重合，并且障碍物的遮挡使得障碍物右侧的传播因子急速减小，在很长一段距离内难以恢复。图4(b) 的观测高度小于地形高度，因此传播因子曲线出现分段现象，这与实际情况相吻合。

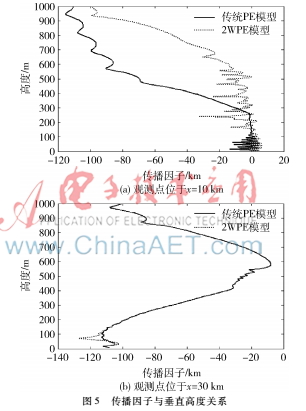
　　图5是传播因子与垂直高度的关系曲线图。从图5(a)中看出，在0~100 m范围内，遇到障碍物后的后向传播能量集中在100 m高度以上区域；高度300 m以上时，2WPE模型的传播因子值大于传统PE模型计算的值，差值主要是由2WPE模型后向传播引起的。图5(b)所示的观察点x=30 km位于起伏地形右侧，不存在后向传播，两种模型的计算方法相同，因此曲线吻合。从图中可以看出，传播因子在高度为600 m左右处，向上和向下的传播都在减小。通过设置多个激励源来扩大传播区域可解决此问题。

　　2.2多个起伏地形对电波传播的影响

　　算例：发射天线高度为HT=50 m，地表为PEC，水平最大距离Xmax=100 km，最大高度Zmax=500 m，三个单刃峰的水平位置分别为30 km、50 km、70 km，对应的高度分别为100 m、200 m、300 m。

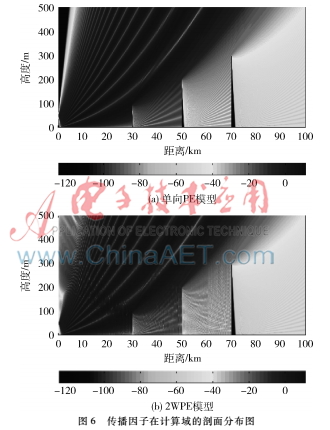
　　图6为传播因子在计算区域的剖面分布图，传播路径上有多个单刃峰。由图可以看出，其现象与单个刃峰情形类似。比较图6(a)和图6(b)发现，两图中左边两个刃峰处的传播因子不同。图6(a)能够清晰看到三个刃峰右侧附近区域电波被遮挡，而图6(b)中左侧两个刃峰处无此现象，这是因为2WPE模型在两个刃峰之间出现反复的后向传播，两个图中距发射点70 km处的刃峰右侧无后向传播，因此都出现电磁盲区的现象。

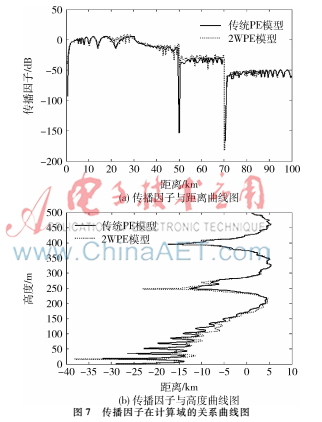
　　图7为传播因子与水平距离和竖直高度的关系曲线图，图7(a)观测点在垂直高度HR=100 m处，从图中很容易看出传播因子的数值在刃峰处迅速减小。在水平方向距原点0~70 km范围内，传统PE模型只计算前向传播，而2WPE模型同时考虑了后向传播，因此2WPE模型得到的传播因子曲线更加准确；水平方向距原点70 km以后两种模型都只有前向传播，因此曲线吻合。此外，由于能量主要集中在前向传播，后向传播的影响相对较小，两种模型预测的结果基本相吻合，在计算精度要求不高的情况下，传统的单向PE模型能够更快预测传播特性而提高效率。图7(b)为传播因子与高度的关系曲线图，其中，观察点在离原点水平距离40 km处。从图中看出，在300 m高度以下，传统PE模型的传播因子数值偏小；在300 m高度以上，没有障碍物遮挡，2WPE模型无后向传播，两种模型的曲线吻合。

3结论

　　双向抛物线方程模型克服了传统抛物线方程模型不能计算后向传播的缺点，本文用SSFT算法求解宽角双向抛物线方程模型的推导和实现过程。采用地形平移法处理地形边界，并且用该模型分析了单个类似高斯型起伏地形、多个刃峰地形等复杂地形对电波传播的影响，将计算的数值结果与单向抛物线方程模型的结果进行比较，得到更准确的电波传播预测结果。

参考文献

　　［1］ LEONTOVICH M A, FOCK V A. Solution of propagation of electromagnetic waves along the earth’s surface by the method of parabolic equations［J］. Journal of Physics, USSR, 1946, 10(1): 1323.

　　［2］ 吴凡. 大气波导中的抛物型方程法研究［D］. 武汉：武汉理工大学，2008.

　　［3］ 袁晓君，林为干. 电波传播的抛物方程近似分析法［J］. 电子科技大学学报，1993,22(1)：4348.

　　［4］ 郭建炎，王剑莹，龙云亮. 基于抛物方程法的粗糙海面电波传播分析［J］. 通信学报，2009,30(6)：4752.

　　［5］ 王昆, 龙云亮, 刘震宇. 基于双向抛物方程逆算法的障碍物定位技术研究［J］.电波科学学报，2015, 30(6):11081115.