0 引言

    在无线接收设备中低噪声放大器(LNA)的噪声性能好坏对整个系统设备有着至关重要的影响，在生产应用中，CMOS技术的重点是努力设计噪声非常小的LNA以及噪声系数优化方法^[1-4]。围绕着LNA噪声系数优化方法分析有着大量的研究，文献[5]深入分析了LNA优化技术，但却忽略了栅极寄生电阻对噪声系数的影响。文献[6-7]指出了一种把噪声系数与功率匹配同时考虑的优化技术，然而却忽略了栅极电感产生的栅噪声影响，且噪声之间的相关性表述不确切。为了保证LNA在恒功耗条件下能够具有优异的噪声性能，本文引入了栅极寄生阻抗和外加电容，依据噪声理论，推导出小信号电路模型的噪声系数表达式，提出了恒功耗条件下的噪声系数优化方法。这一方法对LNA在给定条件下的噪声优化方法设计具有明显的指导意义。同时对提出的噪声优化方法进行MATLAB理论仿真，在ADS软件中对理论结果进行了仿真验证。

1 LNA噪声系数优化方法

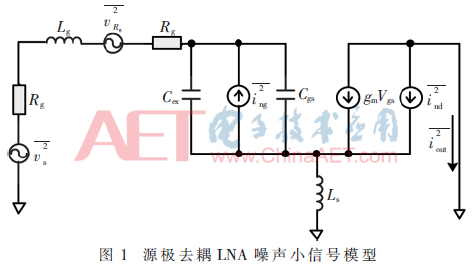
    如图1所示为源极去耦的LNA噪声小信号等效电路模型，其中引入了栅极寄生电阻R_g和外加电容C_ex。栅极电感L_g和栅极寄生电阻R_g在电路品质因数Q_s的提高下，也会随之增加，电路噪声系数势必会有增大的趋势，而外加电容C_ex的作用在低功耗的约束条件下，使得阻抗和噪声同时达到匹配^[8]。因此，在功耗恒定时，为了实现更好的噪声系数优化，栅极寄生电阻及栅极电感的影响在噪声系数中应体现出来。

    噪声系数的定义为：总的噪声输出功率与由输入噪声源引起的输出噪声功率之比^[9]，即：

    这里引入传输函数Δ(jω)和Γ(jω)分别表示源极噪声源与它所引起输出之间的关系和栅极噪声源与它所引起输出之间的关系，使用G_m(jω)来表示晶体管的传输增益。根据传输函数与栅极源极噪声互相关因子，式(1)可以修正为：

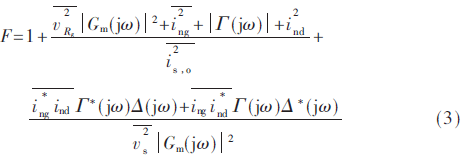
当LNA发生谐振时，通过它的小信号噪声模型可以获得传输函数的表达式。谐振时有ω₀C_t(L_s+L_g)=1，其中C_t=C_gs+C_ex。据此，可以获得传输函数表达式为：

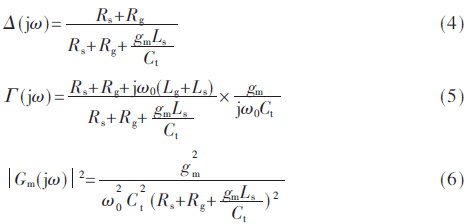
    由式(4)可以看出，由源极噪声引起的噪声功率是一个比例常数，取决于栅极过载电压V_GT=V_gs-V_T，其中V_T是晶体管的阈值电压。在推导噪声系数的过程中，可以做一些定义：D=R_s+R_g+g_m L_s/C_t，L_t=L_s+L_g，R=R_g+R_s和Q_s=ω₀ L_t/R，使得式(4)、式(5)、式（6）书写简便，即：

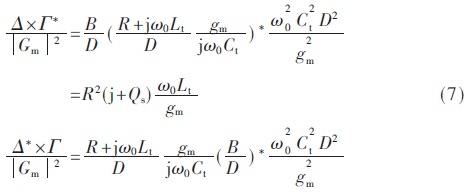
    由于晶体管的两个噪声源都是相关的，据相关系数概念，可由式(2)得到：

    因为噪声电压功率与电流功率都有一个与之相关的噪声电阻，因此上式可以修正为：

    由于考虑到栅极寄生电阻和外加电容对噪声系数的影响以及晶体管品质因数Q_s与功耗之间的关系，据此可以推导出噪声系数的最终表达式为：

2 结果及分析

    以图1作为研究的基本拓扑结构，采用ADS软件以及MATLAB作为仿真设计平台。其噪声小信号模型相关参数为：频率：f=2.5 GHz，直流电压：V_dd=1.8 V，速度饱和电压强度：E_sat=4.7×10⁶ V/m，电子饱和速率：v_sat=8.43×10⁴ m/s，栅极方块多晶硅电阻值：R_sq=10 Ω/sq，栅值宽度：W_f=2.5 μm，晶体管有效沟道长度：L=0.16 μm， 栅源电容：C_gs≤1 pF，相关工艺参数：γ=2/3、δ=4/3、c=j0.395，源极电感：L_S≤2 nH，栅极总电容C_t≤3 pF，直流功耗：P_D=50 mW，栅极螺旋电感品质因素：Q_ind=35。

    图2为恒定功耗条件下噪声系数随电路输入品质因数变化的关系。由图可知，考虑栅极寄生阻抗时，相比未计算栅极寄生阻抗时的噪声系数有一定的下降，这是因为外加电容和栅极寄生电阻，平衡了晶体管自身的噪声与栅极阻抗的噪声，同时外加电容使得源极电感值变小，从而降低了噪声系数，实现噪声和阻抗同时匹配。

    图3是Qs=3.3时仿真结果。从图中可以看出，当频率为2.5 GHz时，LNA输入端的反射损耗S11为-32.718 dB，而反射损耗在-10 dB以下是工程设计中的普遍要求。正向传输增益为14.167 dB。为验证当Q_s=3.3时LNA噪声系数取得最小值，对Q_s在3.3附近取值，利用ADS仿真电路进行仿真验证，得到仿真验证数据如图4所示。

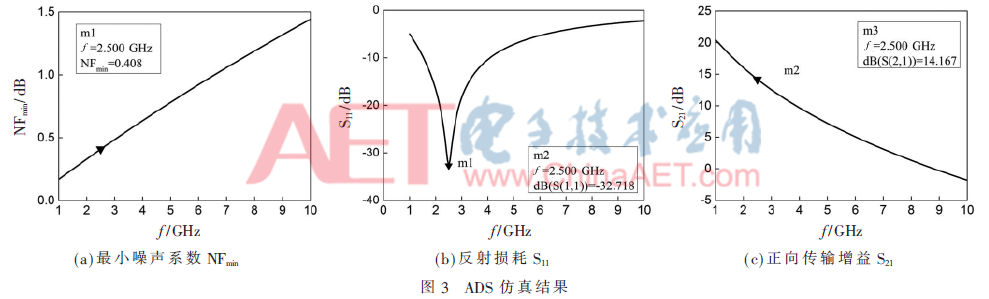
    图4为不同Q_s值条件下噪声系数随频率变化的关系。从图中可以看出，Q_s不同，噪声系数不同，即同一频率基础下Q_s增加，最小噪声系数也相应地增加，具有偏置依赖性；同一Q_s偏置下，随频率的增加成线性比例增加，具有频率依赖性。同时也验证了提出的恒功耗条件下噪声系数优化表达式的理论结果的正确性。

3 结论

    本文基于LNA小信号噪声模型，依据噪声理论基础，推导出此小信号电路的噪声系数表达式，考虑了恒功耗条件下栅极寄生电阻和栅极电感阻抗以及外加电容对噪声系数的影响，提出恒功耗条件下的噪声系数优化方法。同时ADS仿真结果对理论结果进行了很好地验证，证明了其正确性。这一方法对LNA噪声系数优化设计具有指导意义。

参考文献

[1] LI J，HASAN S M R.Design and performance analysis of a 866-MHz low-power optimized CMOS LNA for UHF RFID[J].IEEE Transactions on Industrial Electronics，2013，60(5)：1840-1849.

[2] LAI M T，TSAO H W.Ultra-Low-Power cascaded CMOS LNA with positive feedback and bias optimization[J].IEEE Transactions on Microwave Theory & Techniques，2013，61(5)：1934-1945.

[3] 洪敏，张瑛，于映，等.一种低功耗CMOS LNA优化设计方法[J].南京邮电大学学报：自然科学版，2015，35(1)：114-118.

[4] EVARISTE W T，ADOLPHE M I，DANIEL T，et al.Noise optimization of readout front ends in CMOS technology with PS circuit[J].Asian Journal of Applied Sciences，2015，2(5)：752-761.

[5] SHAEFFER D K，LEE T H.A 1.5-V，1.5-GHz CMOS low noise amplifier[J].IEEE Journal of solid-state circuits，1997，32(5)：745-759.

[6] NGUYEN T K，KIM C H，IHM G J，et al.CMOS low noise amplifier design optimization technique[C].Circuits and Systems，2004.Mwscas '04.the 2004，Midwest Symposium on.2004：I-185-8.

[7] GOO J S，AHN H T，LADWIG D J，et al.A noise optimization technique for integrated low-noise amplifiers[J].IEEE Journal of Solid-State Circuits，2002，37(8)：994-1002.

[8] DENG Z，NIKNEJAD A M.On the noise optimization of CMOS common-source Low-Noise amplifiers[J].Circuits & Systems I Regular Papers IEEE Transactions on，2011，58(4)：654-667.

[9] KIM T S，KIM B S.Post-linearization of cascode CMOS low noise amplifier using folded PMOS IMD sinker[J].IEEE Microwave & Wireless Components Letters，2006，16(4)：182-184.

[10] 刘凤，王军.CMOS低噪声放大器的噪声系数优化[J].通信技术，2011，43(10)：121-125.

作者信息:

王丹丹，王  军，王  林

（西南科技大学 信息工程学院，四川 绵阳621010）