刘阳，胡玉兰

　　（沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159）

        摘要：针对复杂背景下的传统目标轮廓检测算法受图像对比度及亮度变化影响，且存在过多噪声与轮廓弱化等问题，提出一种新的相位一致性周边抑制轮廓检测算法。算法首先根据相位一致性(PC)原理，应用Log_Gabor 构造相位一致性模型，克服了对比度与亮度改变的影响；其次，引入全变差去噪模型，基于相位一致性进行了改进，去除了大量的噪声；最后，提出各向同性周边抑制模型对上述模型进行优化，抑制纹理边缘，使真实轮廓更突出。仿真结果显示，与PC模型和周边抑制算法相比，新算法的精度更高, 明显优于传统方法, 并具有较高的稳定性。

　　关键词：轮廓检测；相位一致性；全变差；周边抑制

　　中图分类号：TP391文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.02.015

　　引用格式：刘阳，胡玉兰. 基于相位一致的周边抑制目标轮廓检测算法［J］.微型机与应用，2017,36（2）：44-47.

0引言

　　轮廓检测在边缘检测的基础上考虑了图像的上下文信息，且广泛应用于机器视觉中，如目标识别［1］等，为此，人们提出了大量的轮廓检测方法，如基于机器学习［2］、灰度差分［3］等。尽管如此，轮廓检测仍有许多困难，远没有得到彻底解决。

　　Canny、Robert算子等方法主要是基于亮度梯度计算的，在自然图像研究中应用范围比较广，但这类算子很容易受到噪声的影响且对于背景纹理复杂的图像很容易受到亮度和对比度的影响，因此仅依靠灰度梯度检测算子很难检测出想要的结果。对于此类方法的缺陷，有学者提出了基于相位一致性原理的边缘检测算法［4］,该类方法充分利用了相位信息对亮度及对比度变化不敏感的优点。但是基于相位一致的检测算法在进行归一化处理时易受到噪声的影响［5］。针对此问题，有学者提出一种全变差去噪模型［6］，能够很好地去除噪声。鉴于相位一致检测模型和全变差去噪模型在边缘描述和噪声分离等方面的优势，将该两种模型结合起来应用到复杂背景下的目标轮廓检测中，在一定程度上解决了上述一致性模型的缺点。但是上述方法检测的结果中仍有大量的纹理信息。为克服背景纹理，有学者提出基于视觉机制的轮廓检测算法［7］，利用Gabor能量进行边缘检测后再进行非经典感受野抑制，实现各向同性周边抑制模型。但上述研究结果中虽然除去了部分纹理，但仍存在轮廓不连续现象。基于上述研究背景及现有算法的缺陷，本文提出一种相位一致性的周边抑制模型，很好地解决了噪声的影响、强纹理去除以及弱轮廓保护的问题。实验结果表明该模型具有可行性及高效性。

1相位一致性

　　1.1相位一致性原理

　　相位一致性原理是：人类视觉感知的图像特征出现在各谐波分量叠合的最大相位处。有学者在实验中证实了相位一致性符合人类视觉感知系统对图像本身特征的认知［8］。相位的特征提取算法是将图像信号进行傅里叶变换后将其分量相位一致的点作为所检测的特征点。如图1所示，傅里叶级数表示方波和三角波，特征点出现在谐波分量叠合最大的0和π相位，非特征点的一致性都因正弦分量的震荡而变化。类似地，三角波的特征出现在相位为π/2，3π/2和5π/2的点处。因此，利用相位一致性算法提取图像边缘不需要对波形进行假设，只需在傅里叶变换域里按照相位一致性原理进行简单的查询。

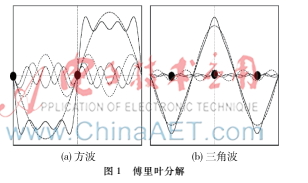
　　对于一维信号I(x)傅里叶展开表示为:

　　I(x)=∑Ancos(nωx+φn0)=∑Ancos(φn(x))(1)

　　式中，An为n次谐波分量的幅度值，ω是常数，φn0为n次谐波分量的相位偏移量，函数φn(x)表示点x处分量的局部相位值。

　　Morrone等人定义了一维信号的相位一致性函数：

　　其中，φ-n(x)是局部相位的加权平均，由式(2)可以看出，PC(x)取值在0与1之间，当所有傅里叶分量均有一致的相位时其取值最大。

　　公式(2)很容易受到噪声的影响，因此文中选用KOVES P［9］改进的相位一致性的计算方法，同时考虑了频率扩展和噪声补偿：

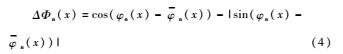　　P

　　式中，W(x)为频率扩展的加权；T为噪声估计；ε为很小的常数；ΔΦn(x)为新的相位偏移函数。

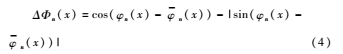
　　由于图像都是二维的，在具体计算中常采用Gabor滤波器来取代最初的傅里叶变换。为了更好地提取背景复杂自然图像的轮廓特征，本文采用Log_Gabor小波［10］的相位一致模型。

　　Log_Gabor小波是一个实部与虚部正交的复小波，零直流分量处为零，在宽带构造中无约束。Log_Gabor小波传递函数为：

　　式中，ω0为中心频率，k/ω0为常量，保持滤波器的形状。

　　若Men、Mon分别代表尺度为n的偶对称和奇对称小波，则信号的响应表达式为：

　　［en(x),on(x)］=［I(x)*Men,I(x)*Mon］(6)

　　在该尺度上的幅度和相位分别表示为：

　　An(x)=en(x)2+on(x)2(7)

　　φn(x)=arctan2(en(x),on(x))(8)

　　则二维相位一致性模型表示为：

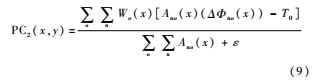
　　式中，o和n分别代表滤波器的方向和尺度。

　　1.2基于全变差模型的相位一致性改进

　　与传统的边缘检测方法相比，虽然相位一致性模型能够检测出比较弱边缘信息，但背景复杂自然图像的细节特征常存在噪声。所以全变差去噪模型的引入能够优化相位一致模型，去除噪声。

　　设混有噪声的图像为u~，去噪后的为u，δ为噪声。去噪模型表示为：

　　u~=u+δ(10)

　　因为解出去噪后的图像是不适定问题，RUDIN L I等人［11］根据有界变差(BV)的特点，使用全变差正则化函数来解决此问题。由于BV空间具有光滑性，可以保证边缘信息不受影响而去除图像中噪声。

　　全变差去噪模型的数学计算式为：

　　minTV(u) + λu~-u2L2(Ω)(11)

　　上式表示为正则项与逼近项的和，作用是约束u的光滑性；λ表示正则化参数，其值为正，目的是使正则项和逼近项保持平衡。研究表明，λ越大，去除噪声效果越小，u和u~越接近。

　　u∈L2(Ω)，全变差表达式为：

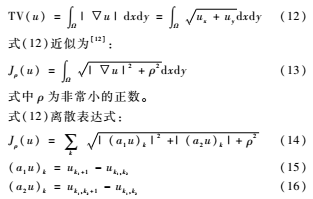
　　由公式(11)~(16)可求解出u~的相似u，u为与原始图像相似的光滑图像，该图像去除了伪边缘。

　　联合式(9)及式(11)，结合TV－L2的相位一致模型表达式：

　　PC′(x,y)=PCu(x,y)PC2(x,y)(17)

　　式中，PC′(x,y)为点(x,y)处的相位一致值，PCu(x,y)为u中点(x,y)处的相位一致值。

2各向同性周边抑制模型

　　上述改进的方法虽然去除了噪声和伪边缘，但是对于背景复杂的自然图像检测结果仍不理想，有纹理存在，所以本文引入非经典感受野模型中的各向同性周边抑制模型对上述算法进行进一步优化。

　　2.1周边抑制

　　描述神经元周边抑制作用的距离权重函数由下面公式构成：

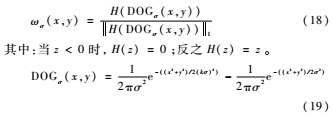
　　式中，·1表示L1范数，H(z)保证算子作用在抑制区域内，也即非经典感受野内，DOGσ(x,y)模拟了非经典感受图2非经典感受野野(如图2所示)的环形区域，并且体现了抑制作用的变化强度，从弱到强再由强到弱。

　　2.2各向同性抑制

　　一些研究表明［12］，在初级视皮层细胞中具有各向同性抑制作用的细胞比具有各项异性抑制作用的细胞比例大，并且各向同性抑制作用模型的模拟更容易，方便实现，计算简单，抑制效果好，因此本文的非经典感受野的模型选择各向同性抑制。

　　各向同性周边抑制参量tσ(x,y)不受外周朝向的影响，仅仅考虑距离因素，表达式如下：

　　tσ(x,y)={PC′(x,y)*ωσ(x,y)}(20)

　　经抑制后输出的响应为:

　　oσ(x,y)=H［{PC′(x,y)－α·tσ(x,y)}］(21)

　　其中，α为抑制参数，α值越小抑制强度越弱，反之，越强。由于一般抑制纹理性边缘需要较大的抑制量，而轮廓对应的抑制量较小，因此从响应oσ(x,y)中能够较容易地提取目标轮廓。

3各新的目标轮廓检测算法

　　算法首先采取相位一致性算法来提取图像的边缘，得到不受对比度及亮度影响的特征值；其次，对上述所得的结果进行全变差去噪处理以使最终轮廓具有很好的光滑性，也为后续的纹理处理提供更好的条件；最后，引入各向同性周边抑制模型(SS)图3新算法流程图来抑制纹理，最终达到保留更多主体轮廓和更少纹理边缘。算法流程如图3所示。

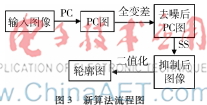
4实验结果与性能评估

　　实验结果采用MATLAB 2013软件编程实现，图像样本采用Grigorescu图像库［12］中的40幅图像，本实验中，将新算法与传统的轮廓检测算法PC算法、各向同性周边抑制模型进行比较，分析本文算法检测性能的优劣。

　　4.1实验结果

　　从图4可以看出，本文算法包含了较少的伪边缘，具有较好的连续性和完整性，真实轮廓显著突出，以图4中第三个图Goat为例， 头部和身上与背景复杂的草相比对比度低，尽管如此，本算法克服了对比度和噪声的影响且很好地抑制了纹理；第二个图的狮子，虽然头部和身体上有很多不规章的毛发，但是本算法检测出的结果连续性和光滑性更好。总之，本算法在克服噪声、抑制纹理和保留低对比度轮廓信息方面的效果更好。

　　4.2定量性能评估

　　GRIGORESCU C等人提出了性能指标——准确率P,用来评估轮廓检测性能［13］。EGT和BGT分别代表地面真实轮廓图像的轮廓像素和背景像素的集合，而ED和BD分别代表检测到的轮廓图像的轮廓像素和背景像素的集合。正确检测的边缘像素的集合E，遗漏边缘EFN及虚假边缘EFP定义公式如下：

　　E=ED∩EGT(22)

　　EFN=BD∩EGT(23)

　　EFP=BGT∩ED(24)

　　轮廓检测器的性能［14］计算公式为：P=card(E)/(card(E)+card(EFP)+card(EFN))(25)

　　漏检率和虚检率分别为：

　　efn=card(EFN)/card(GT)(26)

　　efp=card(EEP)/card(E)(27)

　　card(x)代表集合x中的元素个数。从上面提到的数据库中选出10幅图像计算了其性能指标，对不同模型的性能在表1中做了比较。

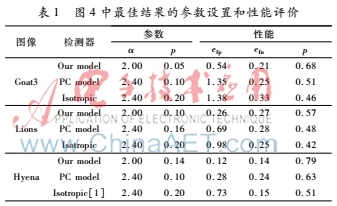
　　表1中结果表明，本文提出的检测器模型提供的P值最高，整体上本文模型在提取图像轮廓时的优势明显高于其他两种模型，检测性能更好。

5结论

　　新的目标轮廓检测算法采用逐层优化的手段实现。相位一致模型克服了对比度及亮度变化对检测结果的影响，全变差模型去除大量的噪声避免了伪边缘的检测。最后用各向同性周边抑制模型进行最终的优化，有效地去除了背景纹理的影响，得到最终的轮廓检测图，主体轮廓边界更加清晰，轮廓检测图的性能得到了优化。新的整性算法简单，高效，通过定量和定性实验分析，该算法是可行的，并且优于其他两种检测算法。

参考文献

　　［1］ LEORDEANU M, SUKTHANKARR, SMINCHISESCU C. Generalized boundaries from multiple image interpretations ［J］. Pattern Analysis and Machine, 2014, 36(7): 1312-1324.

　　［2］ MARTIN D R, FOWLKES C, MALIK J. Learning to detect natural image boundaries using local brightness, color, and texture cues［J］. Pattern Analysis and Machine Intelligence, 2004, 26(5): 530-549.［3］ LIM D H, JANG S J. Comparison of twosample tests for edge detection in noisy images［J］. Journal of the Royal Statistical Society, 2002, 51(1): 21-30.

　　［4］ 肖鹏峰，冯学智，赵书河，等.一种基于相位一致的高分辨率遥感图像特征检测方法［J］.遥感学报，2007,11(3):303-310.

　　［5］ Luo Ding,Zhao Rongchun, Ci Linlin, et al. Phase congruency based edge detection by Hibert filers ［J］. Journal on Image and Graphics, 2004,9(2):139145.

　　［6］ RUDIN L I, OSHER S, FATERMI E. Nonlinear total variation based noise removal algorithms［J］. Physica D: Nonlinear Phenomena,1992,60(1):259-268.

　　［7］ JONES H E, GRIEVE K L, WAND W, et. al. Surround suppression in primate V1 ［J］. Neurophysiology, 2001, 86 (10): 2011-2028.

　　［8］ MAHMOUDI M T. A comparative study of edge detectors for lane detection［C］. Proceedings of the International Conference on Imaging Science, Systems and Technology，2003:526-530.

　　［9］ KOVES P. Edges are not just steps［C］.Proceedings of ACCV 2002. Melbourne, Australia,2002:822-827.

　　［10］ 徐寒. 基于Log_Gabor小波相位一致的掌纹识别算法研究［J］. 制造业自动化，2011,33(4) :4-6.

　　［11］ RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based nosie removal algorithms ［J］. Physica D: Nonlinear Phenomena, 1992,60(1): 259268.

　　［12］ Zeng Chi, Li Yongjie, Yang Kaifu, et al. Contour detection based on a nonclassical receptive field model with butterflyshaped inhibition subregions［J］. Neurocomputing, 2011, 74(10):1527-1534.

　　［13］ GRIGORESCU C, PETKOV N, WESTENBERG M A. Contour detection based on nonclassical receptive field inhibition［J］. IEEE Transactions on Image Process, 2003, 12 (7) : 729-739.