0 引言

    网络编码被证明可以有效提高无线通信系统的频谱利用率^[1]。利用无线网络的广播特性，中继节点可以将收到的两个数据包进行合并，然后同时广播给两个用户节点，从而节省一个传输时隙，每一个用户节点将自己已经发送的数据包和新接收到的数据包进行异或操作，从而得到自己所需要的数据。目前有两种网络编码方式：物理层网络编码^[2]和MAC（Medium Access Control）层网络编码^[3]。物理层网络编码需要精确的时间、相位同步，用户节点需要对功率进行精准的控制。由于MAC层网络编码易于实施，因此本文只研究MAC层网络编码。

    文献[3]首次提出MAC层网络编码的概念，在有线网络的基础上，人们发现无线网络的传输特点更有利于网络编码特性的发挥^[4]。文献[5]利用香农定理给出了理想传输情况下双向中继系统的速率域。文献[6]利用嵌入式Markov模型对基于网络编码的双向中继系统进行了分析，但是该研究没有考虑调度开销因素。文献[7]利用中断概率理论使得系统的吞吐量最大化，但是该研究是在理想的信道传输情况下得出，当链路存在损耗时该传输模式是否最优尚未被研究。

    本文首先提出一种随机网络编码传输策略，将调度开销、缓存有限、链路损耗等因素综合考虑进来，对该系统进行Markov建模，求出该双向中继系统的平均吞吐量、时延等性能的闭式解。最后通过MATLAB仿真对所提模型进行验证，结果显示该理论模型可以精确地对系统进行分析，且本文所提出的传输策略优于已有的传输策略。

1 系统模型

    如图1所示，两个通信终端(U₁和U₂)需要交换数据，由于物理障碍等原因，U₁和U₂之间无法建立直达的通信链路。第三个节点R同时位于U₁和U₂的通信覆盖范围之内。R采用解码转发(DF)的方式，从U₁(或U₂)处接收数据，然后将之传输给U₂(或U₁)。数据帧传输成功概率从U₁到R记为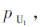从U₂到R标记为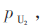从R到U₁标记为p_R1，从R到U₂标记为p_R2。假设U₁和U₂的缓存队列中存在足量的数据等待发送，R将从U₁和U₂处接收到的数据分别存储于缓存的不同区域中，分别标记该缓存队列为L和K。不失一般性，令所有数据包的长度相等，所有节点以等速率发送数据。

2 双向中继传输策略

    考虑有损链路、有限缓存的情况下，本文提出一种实用双向中继网络编码传输策略。U₁、U₂和R以时分多址（TDBC）的方式接入信道进行数据传输。不同于现有的双向中继传输系统，由于不再需要对各节点的通信进行实时调度，因此本节所设计传输策略的确认信息（ACK）将被包含在数据包中进行传输以节省令开销。如图2所示，用户节点和中继节点交替传输数据包。为了区分不同的节点传输，定义两个阶段：T₁阶段和T₂阶段，其中T₁阶段中用户U₁和U₂拥有发送数据的机会，T₂时期内中继节点R拥有发送数据的机会。

    T₁阶段，用户U₁和U₂依次向中继节点R发送一个数据帧，如果R中缓存未满，则R进行数据接收操作，否则保持静止直至下一个时隙到来。如果R进行接收操作且能够正确解码，则将该数据存储于先进先出(FIFO)缓存队列L(或K)中。在T₂阶段，R被允许发送缓存中的数据。本文传输策略采用尽力而为的网络编码方式，此时，若R处两个缓存队列均不为空，R采用网络编码的方式双向转发缓存队列中的数据，R从两个队列中各取一个数据包，进行异或操作，合并成一个新的数据包，然后广播出去，两个用户将接收到的数据与自己先前发送的数据进行异或，消除该数据包中自己的信息，提取到对方所发送的数据；若R处有一个队列为空，R采用传统的单向中继转发模式转发数据；若R处缓存中没有数据，R不发送任何数据，保持静止直至下一个时隙的到来。

3 Markov建模

    选取缓存L和K处的队列实时长度作为马尔可夫链状态的参数，L和K在第i时刻的队列长度记为l(i)和k(i)，其中l(i)=0，1，…，L；k(i)=0，1，…，K。选取两个队列的长度组合s=(l，k)来表示该马尔可夫链的状态，易知该马尔可夫链共有(1+L)(1+K)种不同的状态。由第2节定义可知，该马尔可夫链状态的转移只取决于当前时刻的状态，以及当前时刻数据包的传输成功概率，而与前一时刻的状态以及前一时刻的数据传输情况无关，因此，该状态的转移过程具有无记忆性，服从马尔可夫特性。

    这里π(0)是初始状态概率向量。为了分析平均吞吐量和平均时延，需要求出状态向量π(i)的平均概率E{π(i)}，简记为π。

    在实际通信系统中，中继节点处的缓存队列长度是有限的，故该马尔可夫模型的状态为可数的；又因为所有状态之间可以在有限步数内以非零概率相互到达，因此该马尔可夫链是非周期遍历的。由文献[8]可知，对于状态有限、具有遍历性的马尔可夫状态转移概率矩阵有：

式中，I是单位矩阵，B是所有元素均为1的方阵，b是所有元素均为1的行向量。因此，只需要求出该马尔可夫转移矩阵P即可得出相对应的稳态概率π，进而求出该双向中继系统的吞吐量和排队时延等性能。

    在该双向中继系统传输中，由于考虑了链路损耗，因此每次数据传输不是100%可靠，每个通信节点的数据传输导致的事件结果不再唯一，因此需要针对用户节点和中继节点的数据传输进行单独分析。又由于每次马尔可夫事件均建立在上次事件的基础上，因此该双向中继传输所对应的马尔可夫链状态转移概率矩阵可以利用全概率公式求得。选取用户节点发送数据的开始瞬间为马尔可夫状态参数的观测点，即T₁的开始处。为了便于表达，标记在T₂开始处的队列状态所组成的集合为s′，因此有：

    将式(8）、式(9)代入式(7)，可以得到此马尔可夫链的状态转移概率矩阵，进而通过式(6)可以求得该马尔可夫链各个状态所对应的稳态概率。在此基础上，可以对该双向中继系统的平均吞吐量、排队时延等性能进行数学分析。

4 系统性能分析

5 仿真

    将文献[7]作为参照，令λ=2 000 B，数据发送速率r=11 Mb/s，τ_P=96 μs，τ₁=10 μ滋s，τ_A=11 μs。图3是不同缓存大小下的吞吐量，线为理论值，圆圈为MATLAB仿真值。可以看出理论值和模拟值是相等的，因此验证了上文所构建Markov分析模型的精确性。

    从图3可以看到，考虑信令开销时，本文所提出传输策略要优于文献[7]。另外，当增加中继节点处的缓存资源时，本文所提出传输策略的平均吞吐量得到显著提升，性能增益达到(5.14-4.5)/4.5=14.3%。还可以看到，在缓存增加初期，吞吐量急剧增加，但是随着缓存大小的继续增加，曲线变得逐渐平缓，即：当大于一定阈值时，继续增加缓存所带来的吞吐量增益逐渐可以忽略不计，因此所提出的模型可以用来确定一个较为合理的缓存大小。

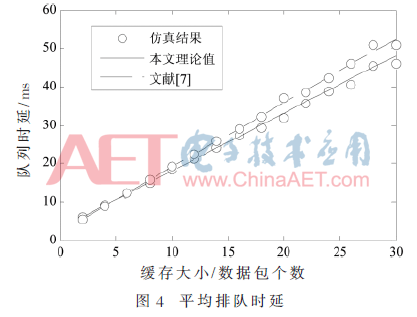
    图4显示，双向中继系统在中继节点处的平均排队时延随着中继节点缓存的增加而呈现接近线性的增加，结合图2可知，无限的增加缓存空间在一定程度上可以提高系统的吞吐量，但是同时也会造成系统的排队时延的线性增加，因此为了提高系统的吞吐量而无限制地增加缓存空间是不明智的。

6 结论

    本文提出了一种考虑链路损耗、缓存有限、考虑信令开销、基于网络编码的无调度双向中继传输策略，构建出Markov分析模型，求出了系统的吞吐量、排队时延的闭式解。仿真表明，在考虑系统的传输开销时，本文所提传输策略要优于已有的传输策略。理论分析和仿真结果还证明，通过适当增加缓存空间可以提高14.3%的吞吐量。

参考文献

[1] LOUIE R H，Li Yonghui，VUCETIC B.Practical physical layer network coding for two-way relay channels：performance analysis and comparison[J].IEEE Trans.Wireless Communication，2010，9(2)：764-777.

[2] ZHANG S，LIEW S C，LAM P P.Hot topic：physical-layer network coding[C].International Conference on Mobile Computing and Networking，MOBICOM 2006，Los Angeles，Ca，Usa，September.2006：358-365.

[3] LI S Y R，YEUNG R W，CAI N.Linear network coding[J].IEEE Transactions on Information Theory，2003，49(2)：371-381.

[4] KATTI S，RAHUL H，HU W，et al.XORs in the air: practical wireless network coding[J].IEEE/ACM Transactions on Networking，2008，16(3)：497-510.

[5] LIU H，POPOVSKI P，DE CARVALHO E，et al.Sum-Rate optimization in a two-way relay network with buffering[J].IEEE Communications Letters，2012，17(1)：95-98.

[6] CHI K，ZHU Y H，JIANG X，et al.Practical throughput analysis for two-hop wireless network coding[J].Computer Networks，2014，60(5)：101-114.

[7] JAMALI V，ZLATANOV N，SCHOBER R.Bidirectional buffer-aided relay networks with fixed rate transmission—part II：delay-constrained case[J].IEEE Transactions on Wireless Communications，2015，14(3)：1339-1355.

[8] GALLAGER R G.Stochastic processes：theory for applications[J].Contemporary Physics，2016，57(2)：1.

作者信息:

沈微微，李  敏，陈  林

（宿迁学院 信息工程学院，江苏 宿迁223800）