史振华

　　(绍兴职业技术学院,浙江 绍兴 312000)

        摘要：针对云计算中无法合理分配资源的问题,提出了采用改进的粒子群算法对其进行分配。由于粒子群算法存在局部收敛速度快,容易陷入局部最优解的情况,从粒子的选择、参数调整和预防过早收敛三个方面进行改进: (1)选择粒子的时候采用适应值最小的粒子,并根据约束函数淘汰不合格的粒子;(2)对惯性因子、个体最优因子和全局最优因子进行改进;(3)通过设定系数来防止算法过早收敛。仿真说明,将改进后的算法运用在云计算方面,在云计算的资源失效、云端用户完成时间和云计算环境下的能量消耗三个方面都优于粒子群算法。

　　关键词：粒子群算法;云计算;资源分配

　　中图分类号：TP393文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.06.019

　　引用格式：史振华. 一种改进的粒子群算法在云计算资源中的研究［J］.微型机与应用，2017,36（6）：62-65.

0引言

　　云计算技术不断发展,现在已经成为了计算机界研究的一个热点。相应地，云计算服务不断发展壮大,其应用领域越来越广泛。云计算是通过互联网技术将海量的IT资源通过有偿的方式提供给云端用户,云计算服务商通过云计算数据中心对云环境中的资源进行统一的管理和分配,最大限度地保证云端负载均衡［1］。由于云计算中的资源是动态的,而云端用户的需求是实时性和多样性的,因此采用固定资源分配的方式无法满足云端用户的需求,云计算服务商提供的服务以资源调度方案最优,整体利益最大化为主要目标。云计算资源调度是一个多任务的NP问题,不同的学者从不同的角度进行了研究。文献［2］提出了采用蛙跳结合神经网络的算法来解决云计算资源分配问题；文献［3］提出将改进的蚁群算法运用到云计算资源调度中,取得了比较好的效果；文献［4］提出了采用改进的布谷鸟算法来进行资源分配,提高了资源的分配效率;文献［5］提出将多维模型与蚁群算法进行相结合来进行云计算资源的分配,取得了比较好的效果；文献［6］提出了生物中的膜计算与蝙蝠算法相结合来解决云计算中的资源分配；文献［7］提出了采用粒子群算法与神经网络相结合的方法分配云计算资源,取得了比较好的效果。

　　本文将粒子群算法运用到云计算中进行资源分配,对于粒子算法存在的问题,分别从粒子的选择、参数调整和预防过早收敛三个方面进行改进。仿真实验说明本文算法相比于基本粒子群算法在资源分配方面有了明显的改进。

1云计算资源简述

　　云计算中的资源调度关系到云计算的运行效率、能量消耗和时间花费等问题。云计算中的每一个云用户是云环境中的一个节点,每一个节点既使用服务又提供服务,云用户之间相互协作实现资源优化配置。因此资源调度算法就成为资源配置的关键,如何设计一个良好的云计算资源算法是十分必要的。云计算资源的调度过程如图1所示。

　　在云计算资源调度中,无论采用什么样的资源调度策略,其目的都是为了更好地使用云计算资源为云用户提供高质量的服务。高效的云计算资源调度目标是在调度资源的时候保证云计算的服务质量(包括服务的时间、效率和可靠性),全面提高资源的利用率和负载均衡,实现利益的最大化。

　　目前,用于云计算资源调度的是启发式的算法,这些算法包括粒子群算法、遗传算法、蚁群算法和人工神经网络算法等,这些算法都具有良好的寻求最优解的性能优点,但容易因自身的原因陷入局部而造成算法收敛。

　2改进的粒子算法在云计算中的应用

　　2.1基本的粒子群算法

　　粒子群算法是通过个体之间的相互协作和相互影响不断地通过迭代来获得最优解的,群体之间的信息共享协助群体进化。设定粒子群算法的目标搜索空间是N维的,粒子群由m个粒子构成,粒子的位置就是一个解,设Vmax为粒子的最大速度,因此群体中的粒子位置和速度采用N维向量来表示。其中,第k个粒子的位置为: Xk=(xk1,xk2,…，xkn)，k∈［1,m］,第k个粒子的速度为Vk=(vk1,vk2,…，vkn)，k∈［1,m］,粒子在迭代过程中的最佳位置就是个体最优解的位置:Pkbest=(Pk1,Pk2,…，PkN),k=1,2,3,…，m,全局最优解为:Gkbest=(Pg1,Pg2，…,PgN)。当找到最优解之后,通过目标函数求出粒子的适应值,通过适应度的大小衡量粒子的位置,然后继续以个体最优解和全局信息解来更新自身的位置改变粒子的运动速度,逐步获得最优解。因此,粒子的更新速度和位置如下:

　　Vki=ηVki+αλ(Pkn－Vkn)+βμ(Pgn－Xgn)(1)

　　Xkn=Xkn+Vkn(2)

　　式中,η为惯性参数,α和β分别是学习因子,α是调节粒子向个体最优位置靠近飞行,β是粒子向群体最优位置飞行,通常情况下,惯性系数η取值为1,λ和μ为相互独立的随机数,Vmax为设置的最大速度。从以上分析可以发现粒子群算法中的最优解是通过粒子之间的协作和相互竞争来获得的,粒子在空间以一定的速度飞行,每个粒子的运动通过个体与群体来不断地调整速度和运动方向,从而获得最优解。

　　2.2粒子群算法的改进

　　在粒子群算法中,没有办法对粒子进行选择,如果出现一些劣质的粒子则会降低算法的收敛速度,影响算法的整体性能。此外,粒子是按照一定的准则进行更新的,根据粒子群的适应度值进行参数调整使得粒子向最优解靠拢,但是在迭代过程中的参数调整对后期的算法影响比较大,有可能导致搜索精度降低，所以参数的设置对于算法的改进具有一定的影响。因此根据粒子群算法实现的流程,本文从几个方面进行改进:(1)对优良粒子进行选择,淘汰差的粒子;(2)对惯性因子、学习因子和群体因子进行调整；(3)通过早熟对算法进行判断和处理。

　　2.2.1选择粒子

　　粒子在进行算法初始化后,都有一个适应值,对于最大优化问题认定适应值大的表示该粒子为优,反之,对于最小优化问题则选择适应度值最小的粒子为优。云计算中的资源调度目标是以花费最少资源,花费最少使用时间为代价来满足用户的需求，因此在选择粒子的时候应该考虑适应值最小的粒子。本文的适应度函数为:

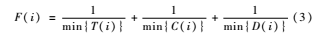
　　式中,T(i)表示第i个资源的时间消耗,C(i)表示第i个资源的成本消耗,D(i)表示第i个资源的带宽消耗。

　　由于粒子算法在运行过程中必须对粒子的运动进行一定的约束,比如限定粒子的速度和运动的区域等条件,因此设定一个约束函数进行解决,约束函数如下:

　　Con(i)=∑hj=1max(0,gj(x))+∑rp=1|hp(x)|

　　s.tgj(x)≥0,j=1,2,…，h

　　hp(x)=0,p=1,2,…，r(4)

　　式中gj(x)是不等式的约束条件,hp(x)为等式约束条件,它反映了粒子距离的区域的程度,约束值越大的粒子应该最先被淘汰。因此选择粒子的策略如下:

　　(1)根据目标函数计算出粒子群中所有的粒子的初始值,并对其进行按照从大到小的顺序进行排序。

　　(2)由约束函数计算出粒子群中的粒子的约束值。

　　(3)根据实际情况对粒子进行淘汰,根据式(3)和式(4)的结果对不合格的粒子进行淘汰,通过设定一定的比例和阈值对其粒子进行筛选。

　　2.2.2参数调整

　　前文已经阐述了粒子群算法中的参数的影响对于粒子的性能是巨大的,由于惯性因子对于算法的优化性能非常直接,当惯性因子的值小的时候,可以加速算法的收敛,当惯性因子的值大的时候,可以跳出局部最优解,学习因子α影响着个体最优的搜索效率,群体学习因子β影响着整个群体的最优的搜索,因此,本文对这三个参数进行调整。

　　(1)对于惯性因子的调整:

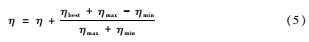
　　式中,ηmax和ηmin分别为惯性因子的最大值和最小值,ηbest为当前状态中的最优值,ηbest+ηmax－ηminηmax+ηmin为整体增量。

　　(2)对于个体学习因子的调整：

　　α=α+φN(6)

　　式中,φ为群体增量系数,N为种群规模，φN为个体学习因子增量。

　　(3)对于群体学习因子的调整：

　　β=β+ψN(7)

　　式中,ψ为群体学习增量系数,N为种群规模,ψN为群体学习因子。

　　2.2.3算法过早收敛判断

　　粒子群算法自身的结构并不复杂,但算法在实现过程中容易出现粒子向着局部最优位置靠近的情况,这样很容易造成算法的局部过早收敛,过早得到局部最优解从而耽误了出现全局最优解的可能,使得算法过早地陷入了早熟的情况。因此算法有必要对早熟进行判断。由于粒子群算法中的粒子的位置决定着粒子适应度,换而言之，粒子的适应度反映了粒子的位置关系,因此可以将粒子的适应度作为是否早熟的条件来进行判断。假设粒子群算法的数目为k,F(i)avg表示粒子群的平均适应度值,Ω表示粒子的聚集度：

　　其中Ω表示粒子群算法聚合离散的程度,Ω的值越大说明聚集度越低,反之,说明聚集度越高。因此Ω数值越小越好,当Ω值越来越大的时候,粒子群中的粒子越来越分散,当大到一定程度的时候,算法满足了终止条件,就陷入了收敛,因此设定一个常数Λ来避免这种情况的发生,当Ω>Λ的时候,就需要进行处理。由于惯性权重比较小的时候是有利于算法收敛的,但式(5)的值不断变大调整,因此需要引入一个系数Γ来约束惯性权重不断地增大。当Ω>Λ时,η=Γη。

　　2.3建立云计算的数学模型

　　在云计算的资源调度过程中,需要从整个网络的带宽、任务响应的延迟、执行时间等方面来进行考虑,既需要让云端的用户请求服务与云服务中的资源匹配,又能够合理高效地满足云计算的资源。设定目标函数为:

　　式中,Time(i)表示运行任务i需要的时间,Delay(i)表示运行任务i需要的延迟,Bandwith(i)表示运行任务i的网络带宽，x+y+z=1。

　　2.4粒子群算法与云计算对应关系

　　将云计算中的云端资源与改进的粒子群中的粒子信息进行对应,云计算中的资源选择的过程就是改进粒子群算法中的粒子淘汰的过程,公式(10)中约束条件对应粒子算法中的选择条件,资源调度中的最优解即为改进粒子群算法中的最优解。

　　2.5算法步骤

　　算法步骤如下：

　　（1）以设计最优的云计算中的资源调度为目标,设定云计算资源与粒子群中的粒子之间的对应关系

　　（2）根据问题确定粒子群数目,设置惯性初始值、最大值和最小值、个体学习因子、群体群体学习因子、最大迭代次数、常数Λ和系数Γ、粒子初始化位置和速度；

　　（3）根据公式(3)选择粒子的初始适应值,淘汰表现不合格的因子；

　　（4）根据粒子群算法要求和公式(5)~(7)不断更新粒子的个体最优和群体最优,迭代次数加1；

　　（5）根据公式(9)判断算法是否会进行过早收敛,如果收敛则进行处理,否则转步骤（4）；

　　（6）判断是否达到最大次数,如果达到则转步骤（9）；否则执行下一步；

　　（7）判断是否收敛,如果收敛则执行下一步,否则执行步骤（4）；

　　（8）确定群体最优对应的粒子信息;

　　（9）根据粒子信息确定最优资源解；

　　（10）算法结束。

3仿真实验

　　3.1搭建实验环境

　　本文实验选择在操作系统为Windows 7,CPU为Inter Core T 6400,内存为2 GB,硬盘为160 GB的台式机上运行。采用Cloudsim仿真平台进行实验。

　　3.2实验结果分析

　　为了进一步说明本文算法相比与改进前的粒子群算法的效率,将本文的算法与基本的粒子群算法从执行云计算的资源失效、云端用户完成时间和云计算环境下的能量消耗三个方面来进行分析。

　　(1)资源失效

　　将云计算资源中的实际能力、存储能力和通信能力作为评价资源淘汰的重要方面,设置惯性因子为2,个体学习因子为1.2,群体学习因子为2.2,最大迭代次数为500次,常数Λ和系数Γ分别为1.5和1，用户任务为20,资源数目为10、30、50、70、90,进行资源调度,选择10次的淘汰资源的平均数作为任务效率的判别标准,结果如表1和图2所示。

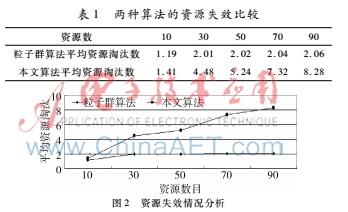
　　从表1和图2中可以发现,基本的粒子群算法的平均淘汰曲线基本上处于水平状,并没有明显的向上发展的趋势,而本文算法的平均资源淘汰曲线呈直线上升,这说明基本的粒子群算法没有淘汰粒子,从而增加了算法在空间和时间上消耗,进一步延迟了算法最优解的产生。而本文算法通过淘汰状态不佳的粒子,减少了算法规模,降低了迭代次数,有利于云计算的资源调度。

　　(2)云端用户完成时间

　　设置虚拟任务为200个,使用本文算法与基本的粒子群算法进行比较,从图3中的曲线来看,本文算法的幅度大于基本的粒子群算法,这说明本文算法通过对自身参数的改进,使得算法的效率更高,从而导致曲线的幅度在开始阶段比较大,随着虚拟任务数目不断增多,算法趋于稳定。从结果来看,本文算法的任务完成时间明显优于粒子群算法。

　　(3)云用户任务能量消耗

　　设置虚拟任务为200个,使用本文算法与基本的粒子群算法进行比较,从图4中的曲线来看,本文算法在能量消耗方面明显低于粒子群算法,这说明本文算法通过对自身过早收敛的改进提高了算法的性能,随着虚拟任务数目不断增多,曲线趋于稳定。这说明本文算法非常适合虚拟任务大的资源调度。

4结论

　　本文将粒子群算法运用在资源调度中,并针对传统的粒子群算法存在的问题进行了改进,将改进后的算法运用在云计算的资源调度中,提高了资源分配效率,在仿真平台中与粒子群算法进行比较，取得了比较好的效果。

参考文献

　　［1］ 李乔.云计算研究现状综述［J］.计算机科学,2011,38(4):32-36.

　　［2］ Chen Xuan.Research of improved shuffled frog leaping algorithm in cloud computing resources［J］.International Jouranl of Grid and Distributed Computing,2016,9(3):24-28.

　　［3］ 聂清彬,蔡婷,王宁. 改进的蚁群算法在云计算资源调度中的应用［J］.计算机工程与设计,2016,37(8):2016-2020.

　　［4］ 叶华乔,丁善婷.基于改进的布谷鸟算法在云计算资源的研究［J］.计算机测量与控制,2014,22(12):4150-4154.

　　［5］ 蒋华,张乐乾,王鑫.基于多维评价模型及改进蚁群优化算法的云计算资源调度策略［J］.计算机测量与控制,2015,23(7):2559-2562.

　　［6］ 宁彬,谷琼,吴钊.基于膜计算的蝙蝠算法在云计算资源调度的研究［J］.计算机应用研究,2015,32(3):830-83.

　　［7］ 赵宏伟,李圣普.基于粒子群算法和RBF神经网络的云计算资源调度方法研究［J］.计算机科学,2016,43(3):113-116.