邵晓艳,李言,李丽红
(华北理工大学 理学院,河北 唐山 063009)
摘要:三支决策是对传统二支决策的推广,它在原有的二支决策中增加了不承诺域,避免了直接做出接受决策或拒绝决策所需承担的风险。但是,从效果上看,不承诺决策和拒绝决策是相同的,不承诺决策同样需要承担风险。基于收益最大化原则的转化方法给出了三支决策中不承诺决策的转化模型,并且比较了收益最大化原则和转化代价最小原则在不同情景中决策上的相同和差异,最后通过实例证明了模型的正确性和可行性。
关键词:三支决策;不承诺决策;转化原则;收益最大化
中图分类号:TP391文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.08.025
引用格式:邵晓艳,李言,李丽红.基于收益最大化的三支决策中不承诺决策转化[J].微型机与应用,2017,36(8):79-82.
0引言
*基金项目:华北理工大学青年科学研究基金(Z201517)三支决策现象在人类社会生活中普遍存在,朴素的三支策略思想简单、方法有效,但是三支决策作为一种理论出现,却是近年的事情。三支决策[1]的概念自提出之后便受到了国内及国际学者的高度关注,他们对三支决策做了大量的研究,但目前的研究重点多集中在三支决策整体上,强调的是三支决策在二支决策的基础上增加了一个不承诺决策[2],实现了对二支决策的改进,并没有系统地对三支决策中的不承诺决策进行深入研究。三支决策中的不承诺决策也是一种决策,同样需要付出代价。
李丽红等人[3]研究了不承诺决策所存在的风险,并给出了基于转化代价最小原则的不承诺决策向二支决策转化的模型。
本文将从收益最大的角度对三支决策中的不承诺决策进行转化。所谓收益最大,是指以转化可能带来的预计收益作为评价函数,然后根据评价函数和阈值对边界域中的元素进行细分。首先,针对边界域中的元素假定两种场景:接受、拒绝,然后比较这两种决策的收益。若转化为接受决策所带来的收益大于转化为拒绝决策所带来的收益,则采取接受决策;若转化为拒绝决策所带来的收益大于转化为接受决策所带来的收益,则采取拒绝决策。基于以上理论,可以将三支决策问题中的不承诺决策转化为二支决策。基于收益最大化的原则,用转化成不同决策所产生的收益作为评价函数,可以进一步完善三支决策理论。
1三支决策的主要知识
为了给概率粗糙集[4]和决策粗糙集中的三个域提供合理的语义解释,姚一豫在2009年提出了三支决策的概念。三支决策的主要思想是将整体分为独立的三个部分,对不同部分采用不同的处理方法,为复杂问题求解提供了一种有效的策略与方法[5]。随着研究的深入,人们发现三支决策并不局限在粗糙集中,它是一种更有效的信息处理模式,可以被应用在不同的领域中,如医疗科学、商业管理学、心理学、认知学、认知科学、计算机科学、工程科学等[6 9]。
三支决策的组成部分包括非空对象集、非空条件集、评价函数及阈值4个方面。
定义1设U={x1,x2,…,xn}是非空有限实体(对象)集,C是有限条件集。基于条件集C,三支决策通过映射f将实体集U分为三个两两互不相交的部分,分别称为L域(Lregion)、M域(Mregion)和R域(Rregion)。即:
Uf{L,M,R}
其中,L、M和R是U的子集,满足U=L∪M∪R,并且L∩M=φ,L∩R=φ,R∩M=φ。
定义2三支决策中的实体评价函数称为决策函数,它的值称为决策状态值。
定义3在基于全序的单评价函数三支决策中,结合阈值(α,β)(0≤β<α≤1)可以构造三支决策规则如下:
(1)如果实体的决策状态值f(x)小于或等于阈值β,则实体属于负域,采取拒绝决策;
(2)如果实体的决策状态值介于两个阈值之间(β<f(x)<α),则实体属于边界域,采取不承诺决策;
(3)如果实体的决策状态值f(x)大于或等于阈值α,则实体属于正域,采取接受决策。
二支决策中只包含正域(POS)和负域(NEG)两部分(即L域和R域),意味着完全接受或完全拒绝,但当现有信息不足以支持做出完全接受或者完全拒绝的决定时,就要使用三支决策,三支决策是对二支决策的推广,它在原有的二支决策中添加了不承诺决策。
2三支决策中不承诺决策向二支决策的转化
在三支决策中需要构造评价函数,并且为决策状态值指定两个阈值。
(1)三支决策中评价函数的构造
以收益最大化作为评价标准时,所选取的评价函数应该满足以下四个条件:
①评价函数中包含了影响收益的大多数指标;
②评价函数中所包含的指标都会影响收益;
③评价函数中所包含的指标可以被定量计算;
④决策结果满足单调性。
收益,从形态来说,可以是有形的,也可以是无形的;从结果来说,可以是物质上的,也可以是精神上的。总之,收益是最关注的部分在做出决策后的结果。
(2)三支决策中阈值的确定
在确定阈值时,需要考虑决策者的心理承受范围,可以立即做出接受决策的决策状态值的下界作为α,必须要拒绝的决策状态值的上界作为β,小于α而大于β的部分则为边界域。在三支决策的不承诺决策向二支决策转化时,转化为接受,是退而求其次的接受,是整体接受域的下确界;转化为拒绝,是迫不得已的拒绝,是整体拒绝域的上确界。即得到的二支决策结果中存在γ,若f(x)>γ,则接受该实体;若f(x)<γ,则拒绝该实体,如表1所示。

(3)基于收益最大原则的不承诺决策转化方法
收益可以包括不同的信息粒度[10],需要从多个角度进行分析。例如,当在决定接受还是拒绝一份新的工作时,需要从工作内容、晋升空间、福利待遇等多个粒度[11]来进行综合判断,以便尽可能准确地预估决策可能带来的收益。
三支决策中不承诺决策的转化步骤如下:
①确定三支决策的分类阈值α、β;
②计算决策函数值f(x);
③针对边界域中的元素,分别计算收益值μPB和μNB;
④当μPB>μNB时,做出接受决策的收益更大,决策结果更合理;当μPB<μNB时,做出拒绝决策的收益更大,决策结果更合理。
(4)三支决策中不承诺决策转化流程图
三支决策中不承诺决策转化流程图如图1所示。
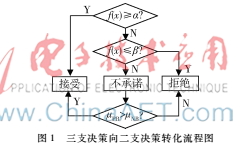
将实现过程进行编程,主要程序伪代码如下:
Begin if(f(x)≥α),
x∈POS(X);//评价函数值大于α,选择正域
else
if(f(x)≤β),
x∈NEG(X);//评价函数值小于β,选择负域
else
x∈BND(X);//评价函数值介于β和α之间,选择边界域
if μPB>μNB
x∈POS(X);//选择正域的收益更大,故选择正域
else
x∈NEG(X);//选择负域的收益更大,故选择负域
End
(5)基于转化代价最小原则与基于收益最大原则的对比
之所以会产生不承诺决策,主要是因为现有信息不足以做出承诺决策,只有随着有效信息的增加,才能够将不承诺决策转化为承诺型决策。在对不承诺域中的元素进行转化的时候,由于信息不足,因此无论转化为接受决策还是拒绝决策都同时存在着风险与收益。
基于转化代价最小原则与基于收益最大原则的主要差别在于对风险或收益的敏感度不同。比如冒险主义者会更加关注收益,更适用于收益最大原则;而保守主义者会更加关注风险,更适用于转化代价最小原则。具体对比如表2所示。

①由表1可以看出,接受决策风险大,同时收益也大时,基于转化代价最小原则会选择拒绝决策(拒绝决策风险更小),基于收益最大原则会选择接受决策(接受决策收益更大);
②接受决策风险大,同时收益小时,两种原则均会选择拒绝决策;
③接受决策风险小,同时收益大时,两种原则均会选择接受决策;
④接受决策风险小,同时收益小时,基于转化代价最小原则会选择接受决策(接受决策风险更小),基于收益最大原则会选择拒绝决策(拒绝决策收益更大)。
当某一种决策风险大(小),同时收益小(大)时,两种原则的选择是一样的;当风险与机遇并存时,两种原则会选择不一样的策略。而在现实生活中,后一种情况更为常见。
3应用实例
随着年龄的增长,“大城市还是小城市?”成为了许多“*漂”一族面临的问题。比如小张和小李就因为结婚之后何去何从产生了分歧。小张一直有做公务员的想法,并最终成功地在远离自己家乡的西北地区找到了一份事业单位的工作。而小李身为21世纪受过高等教育的新时代女性,并不认为“嫁鸡随鸡,嫁狗随狗”是理所当然的事情,加上自己所学专业的限制,留在一线城市更容易有发展空间,所以一直坚持“漂”着。两人都明白结婚之后,异地不是长久之计,但谁也不肯放弃自己的工作。在目前的情况下,让小张放弃自己的工作太不现实,只能是小李考虑是否接受远离自己家乡的新工作,所以请根据目前的形势,帮助小李进行决策,并且给出最终结果及理由。
(1)小李坚持“漂”着,没有讨论的必要,问题结束。
(2)小李在决定是否接受新工作时,主要从父母、小家、生活成本、人际关系、养老、工作内容、工作未来发展、薪资待遇、工作压力9个粒度来考虑。为便于计算,假设小李目前月薪1万元,如果新工作月薪高于8 000元,则愿意接受新工作;如果新工作月薪低于4 000元,则拒绝新工作。经过面试,小李所拿到的offer中,最高月薪为5 000元,则此时的决策为“暂不考虑新工作”。
①对于小李来说,选择一个合适的男朋友是可遇而不可求的,一旦放弃,沉没成本太高,而且不能保证以后遇到的更好。考虑到实际情况中可能的影响因素有生活、工作、父母、小家4个方面。其中,生活又可以细分为生活成本、人际关系、养老3个方面;工作可以细分为未来发展空间、时间是否自由、工作压力3个方面;父母主要是离家太远,照顾父母不方便;小家主要面临的也是距离问题。综合考虑得出各个指标及其权重如表3所示。

其中,各因素细分如表4、表5所示。
②拒绝新工作的优点有:生活上人际关系简单、工作上发展空间大、离家近。
③接受新工作的优点有:生活成本低、老年生活有保障、工作压力小、时间自由,并且可以解决异地问题。
④将以上信息转化为二维表的形式,存入Excel,如表6所示。

⑤编写代码如下:
Sub decision()
Sheet1.Select
n = Range("A1").End(xlDown).Row()
Fori = 2 To n
If Cells(i, 5) = "接受" Then
POS = POS +Cells(i, 3) * Cells(i, 4)
Else
NEG = NEG +Cells(i, 3) * Cells(i, 4)
End If
Next
If POS > NEG Then
MsgBox ("接受决策可带来的幸福指数为" & Format(POS, "0.0#") & "," & vbCrLf & "拒绝决策可带来的幸福指数为" & Format(NEG, "0.0#") & "," & vbCrLf & "所以应选择接受决策!")
Else
If POS < NEG Then
MsgBox ("接受决策可带来的幸福指数为" & Format(POS, "0.0#") & "," & vbCrLf & "拒绝决策可带来的幸福指数为" & Format(NEG, "0.0#") & "," & vbCrLf & "所以应选择拒绝决策!")
End If
End If
End Sub
执行后,所得结果为:
“接受决策可带来的幸福指数为0.6,拒绝决策可带来的幸福指数为0.4,所以应选择接受决策!”
此时,虽然评价函数处于边界域的范围内,但给出“接受决策”的综合权重大于“拒绝决策”。所以,在必须要立即做出决策的情况下,边界域“暂不考虑新工作”转化为二支决策中“接受新工作”,可以使得幸福指数更高。
4结论
本文基于收益最大化原则对三支决策中的不承诺决策进行了细分,最后用实例验证模型的实用性。而收益最大化是博弈[12]的基本观点,将博弈与三支决策的结合还可以进行更深入的研究。
参考文献
[1] Yao Yiyu. Threeway decision: an interpretation of rules in rough set theory[C]. Proceedings of Rough Sets and Knowledge Technology: 4th International Conference, RSKT 2009, Gold Coast, Australia, 2009:642-649.
[2] 杜丽娜. 三支决策理论与应用研究[D]. 新乡: 河南师范大学, 2015.
[3] 李丽红, 李言, 刘保相. 三支决策中不承诺决策的转化代价与风险控制[J]. 计算机科学, 2016, 43(1): 77-80.
[4] Yao Yiyu. The superiority of threeway decisions in probabilistic rough set modes[J]. Information Sciences, 2011, 181(6): 10801096.
[5] 于洪, 王国胤, 李天瑞, 等. 三支决策: 复杂问题求解方法与实践[M]. 北京: 科学出版社, 2015.
[6] 贾修一, 商琳, 周献中, 等. 三支决策理论与应用[M].南京: 南京大学出版社, 2012.
[7] 刘盾, 李天瑞, 李华雄. 粗糙集理论: 基于三支决策视角[J]. 南京大学学报(自然科学版), 2013,49(5):574-581.
[8] 谢骋, 商琳.基于三支决策粗糙集的视频异常行为检测[J].南京大学学报(自然科学版), 2013, 49(4): 475-482.
[9] 黄顺亮, 王琦. 基于三支决策理论的客户细分方法[J]. 计算机应用, 2014,34(1): 244248.
[10] 张里博, 李华雄, 周献中, 等. 人脸识别中的多粒度代价敏感三支决策[J]. 山东大学学报(理学版), 2014,49(8):48-57.
[11] 李建林, 黄顺亮. 多阶段三支决策垃圾短信过滤模型[J]. 计算机科学与探索, 2014,8(2): 226-233.
[12] 徐文. 一本书看懂博弈论[M]. 北京: 新世界出版社, 2010.

