马健超1,2，陈国栋1,2，周霆1,2

　　（1.福州大学 物理与信息工程学院，福建 福州 350116；2.福州大学 计算机图像图形研究所，福建 福州 350116）

　　摘要：虚拟手术系统研究是计算机图形学的一个重要领域，为了提高肌肉纤维纹理合成的真实感与实时性，文章采用了基于场向参数化的方法，并结合最光滑方向场进行了三维模型上的肌肉纤维纹理映射与合成，通过布置奇异点，模拟肌肉纤维损伤的状态。该系统实现了场向参数化的可视化及肌肉纤维纹理合成的简单交互，实验结果表明，系统的实时性与真实感均得到提高。

　　关键词：虚拟手术；场向参数化；最光滑方向场；纹理合成

　　中图分类号：TP391.41文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.09.006

　　引用格式：马健超，陈国栋，周霆.基于场向参数化的肌肉纤维纹理合成研究［J］.微型机与应用，2017,36（9）：18-21.

0引言

　　随着现代医学技术和计算机技术的发展，借助计算机图形技术分析处理医学问题成为了医学研究和计算机图形技术的热点，虚拟手术就是其中一个重要的学科发展方向，其具有沉浸性、交互性等特点［1］。

　　在计算机图形学中，纹理的应用是增强真实感的有效方法，对于三维表面纹理合成，实现的目标是将二维纹理映射到三维表面，并且不产生走样和扭曲。现有方法通常是把表面领域通过参数化方法展平，然后沿着表面局部坐标系进行采样，将采样得到的平面领域与样本纹理的领域进行比较［2］。Praun［3］等人提出用重叠纹理技术来合成三维表面纹理，该算法需要较多的人工干预；Wei［4］等人把表面纹理的颜色信息存储在模型的顶点上，根据松弛算法生成方向场来定义三维表面局部坐标系，但合成速度不理想；Turk［5］等人使用密集模型保存丰富纹理细节，对每个目标领域进行局部参数化，合成速度较慢。这些方法都从图像特征的统计相似性来解决问题，但不能很好地绘制出肌肉纤维纹理的特点。骨骼肌由肌腹和肌腱构成，肌腹由大量的横纹纤维构成，不同部位间纤维方向差异较大，而肌腱由腱腱纤维构成［6］，肌肉损伤的表现为肌肉纤维沿筋膜面羽毛状扩展，或向邻近肌肉扩展［7］。

　　为了提高虚拟手术中肌肉纤维仿真的真实感和实时性，本文从几何学的角度来看待这个问题，采用最光滑方向场与场向参数化相结合，在Ray［8］等人的全局场面参数化方法的基础上，允许加入新的奇异点，以此来仿真肌肉损伤，并省略了旋度校正和单位化约束，使用一个简单的凸二次能量来规划问题，算法速度得到提升，通过简单的交互，可以实时改变最光滑方向场的方向，从而得到三维模型上不同方向的肌肉纤维纹理，可应用到虚拟手术中。

　　本文实现的整体算法流程如图1所示，通过读取三维网格模型，如OBJ格式，使用重新定义的狄利克雷能量来获取最光滑方向场，使用该方向场进行参数化，得到相应的纹理坐标，最后使用模型加载库Assimp及OpenGL等开源库进行纹理的合成。

1最光滑方向场

　　1.12-方向场

　　本文中的方向场指的是单位长度的矢量场，方向场的度n指的是曲面上每一点有n等间隔分布的方向场。如图2所示，左图为n为1时，即传统意义上的场;右图为n为2时，称为2方向场［9］，每一点由两个方向相反的单位矢量组成。这些方向场通常存在奇异点，即方向场在该点无法光滑地变化，注意，本文产生的方向场将自动地布置奇异点的个数与位置。

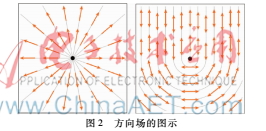
　　本文将曲面M上的一点的切空间视为复数域C的副本，其上的切矢量可用复数乘以一个基矢量来表示，若以实轴为基矢量，再通过平方，得到一个不需要考虑单位约束的方向场的表示方法，为：

　　u=z2=ei2kπ,k=0,1(1)

　　1.2光滑能量

　　通过使用狄利克雷能量来测量2方向场ψ的光滑度［10］，表示协变导数，也就是曲面上的列维奇维塔联络，表示为：

　　但方向场中，在奇异点处该能量变得无限大，导致该公式失去意义，而每一个2方向场可写成一个比例因子与单位方向场的乘积，即：

　　ψ=aφ(3)

　　将所有的ψ中最小的狄利克雷能量定义为2方向场的能量，即式(4)，此时奇异点处的能量将变为零，从而解决了上述的问题。

　　遍历所有方向场，从而得到全局最小化的方向场，也就是最光滑方向场，由于经过了缩放的2方向场的集合与2矢量场的集合是没有区别的，所以可以替而求解。

　　这意味着一个最小特征值的问题，三维网格上所有方向场ψ都是分段线性的，将其表示为基底的复线性组合，V代表点集。

　　式(5)的问题转化为求解特征向量的问题。等式(7)中，A是一个相对于分段线性基底Ψi的埃尔米特矩阵，M是埃尔米特质量矩阵，使用逆幂迭代法来求解，得出最光滑方向场。

　　Au=λMu(7)

　　2场向参数化

　　2.1坐标函数

　　首先需要选择参数化后的坐标函数的表达形式，Ray［8］等人和Zhang［11］等人提出使用复数域的矢量值函数，其角度分量提供最终的坐标，但每一点有一个四阶的惩罚项，导致了非凸规划问题，所以本算法忽略了这一项，同样使用一个复数域的矢量值函数ψ，用其幅角α作为参数化后的坐标，为：

　　α=argψ(8)

　　设定最光滑方向场为X，每点的单位化函数为：

　　φ=eiα(9)

　　角α只沿着方向X以速率ν来变化，通过微分，得到

　　dφ=iωφ(10)

　　这意味着通过求解该等式可以得到角速度ω，但需要方向场总是可积的，因此考虑它的L2残差：

　　其中算子c=d－iω恰好是曲面M上的一个联络，ε可以被认为是在一个复变函数上的狄利克雷能量，所以定义单位化函数φ能量为比例函数a下，所有可能的最小的狄利克雷能量：

　　在单位化函数φ上的能量极小化是等价于在所有复变函数ψ上的狄利克雷能量极小化：

　　因此对应为一个标准的求解特征值的问题，ψ为特征函数，Δs为薛定谔算子。

　　Δsψ=λψ(14)

　　2.2不可定向特征

　　方向场中存在不可定向的点，即在奇异点有不可定向的特征，引进Kalberer［12］等人提出的二次覆盖的概念。除了奇异点之外，二次覆盖看起来就像原曲面的副本，但算法中并没有实际地去构造二次覆盖，只是用这一思想来解决奇异点的问题。图3为二次覆盖于原曲面的示意图，MD为二次覆盖，M为原曲面，τ称为片交换函数，ρ将二次覆盖映射回原曲面，曲面M上的线场，在MD上任意选择其中一个方向的场。

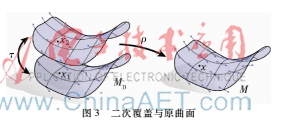
　　2.3离散化

　　三角网格上，每一个顶点i∈V，用单位切矢量Xi和目标线频率νi∈R+共同定义了矢量Zi=νiXi，离散化算法的具体步骤如下：

　　输入：二维单纯复形K（三角网格）。

　　过程：

　　（1）将Z投影到每一条边上，得到角位移ω；

　　（2）构建类拉普拉斯矩阵A，元素由ω决定；

　　（3）求矩阵A最小特征值对应特征向量ψ 。

　　输出：每一个面上，通过ψ和ω得到计算纹理坐标α。

　　首先求得角位移ωij，即边矢量与输入矢量场的内积

　　的平均值。

　　ωij=∫ijω=12(〈eij,Zi〉+〈eij,Zj〉)(15)

　　然后每个三角形构建类余切拉普拉斯矩阵，即薛定谔算子的离散化。该矩阵A是正定对称，与余切拉普拉斯矩阵有相同结构，对于每个正则边ij∈E，非对角块为：

　　Aij=－wij［eiωij］,sij=－1

　　－wij［eiωij］,sij=+1

　　Aji=ATij(16)

　　矩阵A的对角块为：

　　Aii=∑ij∈E［ωij］(17)

　　块对角集总质量矩阵为B，用Aijk表示三角形ijk的面积，对角元素为关联三角形总面积的三分之一。

　　Bii=13∑ijk∈FAijk(18)

　　存在ψi=ai+bii的某个值来使ε最小，用ai,bi∈R值交替组成的一个矢量x，通过求解式(19)的最小特征值对应的特征向量x，使用乔里斯基分解矩阵A，然后应用逆幂法来求解。

　　Ax=λBx(19)

　　求得ψ后，如果仅通过式(8)来求最终的坐标函数α，将产生畸变与扭曲，因此采用旋转形式进行调整，最终坐标为：

　　αjki:=arg(ψi)

　　αkij:=arg(ψi)+σij

　　αijk:=arg(ψi)+σik(20)

3结果与分析

　　3.1编程环境与开源库

　　本课题使用系统为Window 7，编程环境为VS2012，处理器为2.40 GHz，内存8 GB，显卡为AMD Radeon 6550M。采用了开源库SuiteSparse来实现对稀疏矩阵的运算，选用了模型加载库Assimp，选用的三维模型格式是OBJ格式，还有OpenGL及其扩展库GLUT和GLEW处理窗口的创建、基本的交互，使用着色语言GLSL编写了顶点着色器和片段着色器。

　　3.2纹理合成结果与分析

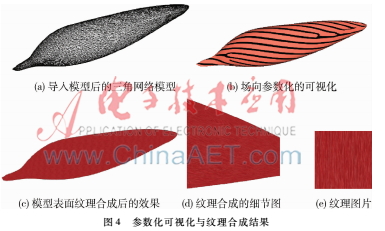
　　图4展示了整个纹理合成的过程，使用模型的面片数为6 142片，（a）为导入模型后显示的三角网格模型；（b）为场向参数化的可视化，可看到奇异点（分叉点）；（c）为模型表面纹理合成后的效果；（d）为纹理合成的细节图，可以看到纹理的方向与方向场一致；（e） 为所使用的纹理图片。图5为图4的2方向场经过旋转90°后的可视化结果，从右图可以看到肌肉纤维纹理的方向已经发生了改变，但是同样与方向场方向保持一致。

　　图6展示的是参数化中奇异点与纹理合成后细节的对比，使用的模型的面片数为15 418片，可以看到纹理在奇异点处发生了分叉，但总体还是保持连续的，以此来模拟肌肉的轻微损伤，左图为场向参数化的可视化，右图为奇异点处的纹理细节。

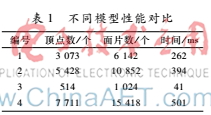
　　通过对不同面片数的模型进行实验，得到了以下的对比数据，表1表明了面片数从1 K~16 K的几种情况下，纹理合成所需要的时间基本控制在0.5 s以内，这样的性能是符合进行实时操作和交互的。表2通过与其他算法的对比，列出了部分数据，表明了本文所使用的算法性能得到提升，计算所需时间平均缩短为算法1的35.2%。

4结论

　　本文基于场向参数化的方法，结合了最光滑方向场，并使用了一系列开源库，实现了对肌肉纤维纹理的合成，最终的系统能够实现实时操作与交互，在保证真实感的同时，也证明了所使用算法的性能有较大的提高，为虚拟手术中肌肉手术的场景的进一步研究提供了条件。

　　参考文献

　　［1］ 邢英杰, 张少华, 刘晓冰. 虚拟手术系统技术现状［J］. 计算机工程与应用, 2004, 40(7):88-90.

　　［2］ 韩建伟. 基于样本的三维表面纹理快速合成技术［D］. 杭州：浙江大学, 2009.

　　［3］ PRAUN E,FINKELSTEIN A,HOPPE H. Lapped textures［C］. Proceeding of ACM SIGGRAPH 2000.New York,USA:ACM Press/AddisonWelsey Publishing Co.2000:465-470.

　　［4］ WEI L,LEVOY M. Texture synthesis over arbitrary manifold surfaces［C］.Proceedings of ACM SIGGRAPH 2001.New York,USA:ACM,2001:355-360.

　　［5］ TURK G. Texture synthesis on surfaces［C］. Proceedings of ACM SIGGRAPH 2001.NY, ACM,2001:347-354.

　　［6］ 席占国, 乔亚亚, 沈素红. 超声诊断肌肉损伤的临床价值［J］. 医药前沿, 2014(18):206207.

　　［7］ 刘亚娟, 冉艮龙, 叶伦,等. 大腿肌肉损伤的MRI诊断［J］. 西南国防医药, 2015, 25(11):1222-1224.

　　［8］ RAY N. Periodic global parameterization［J］. Acm Transactions on Graphics, 2006, 25(4):1460-1485.

　　［9］ VAXMAN A, CAMPEN M, DIAMANTI O, et al. Directional field synthesis, design, and processing［C］． SIGGRAPH Asia， 2016:1-30.

　　［10］ LIU B B, WENG Y L, WANG J N, et al. Orientation field guided texture synthesis［J］. Journal of Computer Science and Technology, 2013, 28(5):827-835.

　　［11］ ZHANG M, HUANG J, LIU X, et al. A wavebased anisotropic quadrangulation method［J］. Acm Transactions on Graphics, 2010, 29(4):157-166.

　　［12］ KLBERER F, NIESER M, POLTHIER K. Stripe Parameterization of Tubular Surfaces［M］. Topological Methods in Data Analysis and Visualization, 2010.