逄淑玲,王晓升
(山东女子学院 信息技术学院,山东 济南 250300)
摘要:文章研究了一种多核架构下基于OpenMP的Dijkstra并行算法,以Dijkstra算法为基础设计并行程序。对传统Dijkstra算法进行分析,明确优化方向,再利用OpenMP开发工具对并行程序进行优化调试。结果表明,文中算法易于操作,并充分利用了多核处理器并行计算的优势,提高了算法的运行效率,验证了算法的优越性。
关键词:多核;Dijkstra算法;OpenMP;并行算法
中图分类号:TP312文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.09.008
引用格式:逄淑玲,王晓升.Dijkstra算法的并行实现[J].微型机与应用,2017,36(9):25-27.
0引言
随着多核的发展,串行执行程序的缺点暴露无遗,传统的Dijkstra算法是串行算法,搜索过程易懂,程序设计简单,但大量内存空间与计算时间的耗费成为此算法的瓶颈,而有效解决的途径之一就是并行计算。为将计算能力最大化,需将一个应用程序划分为多个相对独立的任务并交由多个计算核执行。为从语言成分上直接支持并行,完全摆脱串行语言的束缚,设计了一种全新的程序设计模型,该并行算法与以往传统算法相比能够更有效地提高运行效率,充分发挥高性能多核处理器的功效。
1OpenMP
OpenMP是一种支持跨平台共享内存方式的多线程并发编程模型,开发过程中无需考虑数据分布,具有良好的可移植性、可扩展性,同时支持C、C++和FORTRAN语言。OpenMP提供一系列体系结构和编程平台,建立简洁高效的编程指导命令和并行编程方式,并提供各类串行程序并行化的可行方案[1]。OpenMP不是独立的并行语言,通过在适当位置加入编译指令和运行库函数来并行化串行程序。OpenMP从主线程开始执行,一直串行地执行该线程,当线程某些点需要并行执行时,程序则派生出额外的线程,组成一个线程组,这些线程在并行域的代码区中并行执行,线程到达整个并行区域的末尾时等待,直到整个线程组都到达,最终相连接,这时只有主线程继续执行直到下一个并行区域或程序结束[2]。举例说明[3]:
int main(int argc,char*argv[]){
#pragma omp parallel for
for(int i=0;i<10;i++)
{
printf(“i=%d/n”,i);
}
printf(“finished.\\n”);
return 0;
}
这段程序就是使用OpenMP编译指导语句“#pragma omp parallel for”将for循环里的内容并行执行,从而提高效率。
2Dijkstra最短路径算法
2.1算法思想
Dijkstra算法是典型的单源最短路径,以起始点为中心向外层层扩展,直到拓展到终点为止。假设Len(v)表示一个顶点到给定顶点U的最短距离,w(u,v)表示两个顶点间的距离。给出两个顶点V1、V2,求两顶点之间最短距离。算法描述如下[4]:
(1)给定顶点V1,标记这个顶点并初始化所有的顶点,将顶点V1放入集合S。
(2)对于集合S中的所有顶点Vi,计算Vi相邻的所有顶点Uj的md(ui,vi)=w(ui,vj)+Len(vj)值并找出最小的md(u,v)值的顶点U,将顶点U放入集合S中。
(3)重复上述步骤,直到将目标顶点V2放入集合S中,即可求出顶点V1到V2间的最短距离,得到最短路径[5]。
Dijkstra最短路径算法流程图如图1所示[4]。
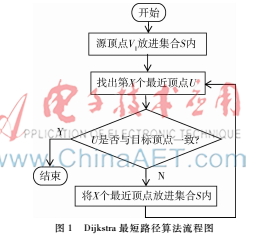
2.2算法分析
通过对该算法的分析得出该算法的不足之处,在每次迭代中,未标记节点以无序的形式存放在一个数组或一个链表内,每次选择最短路径节点都必须把所有未标记节点扫描一遍,当节点数目较大时,这将成为制约计算速度的关键因素。
3基于OpenMP的并行Dijkstra算法
3.1算法的并行化思想
在编程时,代码并行执行不仅限于某个函数的并行化,而是函数内部也需创建线程使关键计算并行执行。频繁创建线程会使工作开销额外增加[6],借助OpenMP在有效的并行化程序的同时也可解决多核编程时线程创建问题。
(1)Dijkstra并行算法设计思想
从Dijkstra最短路径算法可看出,集合S每次循环迭代之后定点个数都会加1,每次迭代都依赖于上次迭代的结果,循环之间存在依赖关系,所以外层循环不能直接并行化[7],因此提出对内层循环并行化。每个线程计算一个顶点的所有边,从中取得最小边并保存在一个数组的不同位置,然后从数组中找出最小的值,得到最近距离的一个顶点[8]。继续执行外层循环,直到找到最近距离顶点和目标节点为止。
(2)并行算法的程序设计流程图[4]如图2所示。

3.2并行算法设计与实现
Dijkstra算法的并行化通过两部分实现:Parallel_GetShortestPath()函数实现主算法流程,SearchNextVertex()函数实现并行计算第M个最近顶点的算法流程[9]。并行算法的实现代码如下[4]:
#pragma omp parallel for
num_thread(pgraph>nnodecount,MIN_ITERATOR_NUM))
for(i=0; i<pGraph>nNodeCount; i++)
{
pGraph>ppNodeArray[i]->nMagic=-1;/*初始化为-1,表示未计算过最短路径的总距离*/
pGraph>ppNodeArray[i]->pMagic=NULL;/*指针为空*/
}
ppSNode[0]=pSrcNode;
ppSNode[0]->nMagic=0; /*初始化为0*/
ppSNode[0]->pMagic=NULL;
for(x=1; x<pGraph>nNodeCount; x++)/*x从1开始循环执行*/
{
DISTANCE nTotalDis;
GRAPHNODE *pTNode;
pTNode=NULL;
NTotalDisGRAPH_MAX_DISTANCE;
SearchNextVertex(pGraph,ppSNode,x,ppNode,pnDis);
INT index=-1;
for(i=0;i<x;i++)
{
if(nTotalDis>pnDis[i])
{
nTotalDis=pnDis[i];
index=i;
}
}
if(index !=-1)
{
pTNode=ppNode[index*2];
pTNode>nMagic=nTotalDis;
pTNode>pMagic=ppNode[index *2+1];
if(pTNode==pTagNode)
{
nTagDis=nTotalDis;/*计算出源节点到目标节点的最短路径*/
Break;
}
}
else{ /*最短路径总是存在的,此处应该不会被执行*/
break;
}
ppSNode[x]=pTNode;
}
free(ppNode);
free(pnDis);
free(ppSNode);
return nTagDis; /*返回目标节点到源节点的最短路径*/
}
4实验与结果分析
为验证并行化后Dijkstra算法的性能,设计实验进行验证,分别采用传统的Dijkstra算法与并行化的Dijkstra算法进行实验,测试了不同节点数和弧段数下运行时间分析对比,评估出并行化后的性能[10],结果如表1所示。

从表1中可看出,在执行相同节点数与弧段数的情况下,并行Dijkstra算法比串行Dijkstra算法更加省时,大幅度提高了运行速度。
5结论
本文对传统Dijkstra算法进行分析,为节省计算机存储空间,提高运行效率,在OpenMP模型下对Dijkstra算法的并行设计进行了研究,通过数据的采集与分析验证并行化后Dijkstra算法的性能,结果表明:该并行算法与以往传统算法相比能够更有效地提高运行效率,充分发挥高性能多核处理器的功效。
参考文献
[1] 王树西,吴政学.改进的Dijkstra最短路径算法及其应用研究[J].计算机科学,2012,39(5):223-228.
[2] 王智广,王兴会,李妍.一种基于Dijkstra最短路径算法的改进算法[J].内蒙古师范大学学报(自然科学汉文版),2012,41(2):195-200.
[3] 彭曦,顾炳根,李展涛.基于多核的OpenMP并行程序设计[J].硅谷,2010,(16):97-98.
[4] 周伟明.多核计算与程序设计[M].武汉:华中科技大学出版社,2009.
[5] 龚向坚,邹腊梅,胡义香.基于OpenMP的多核系统并行程序设计方法研究[J].南华大学学报(自然科学版),2013,27(1):64-68.
[6] 叶仕灏,王伊蕾.一种优化Dijkstra算法的研究[J].计算机应用与软件,2011,28(9):272274.
[7] 李健.基于Dijkstra最短路径算法的优化研究[J].渭南师范学院学报,2009,24(5):6164.
[8] 计会凤,徐爱功,隋达嵬.Dijkstra算法的设计与实现[J].辽宁工程技术大学学报(自然科学版),2008,27(S1):222-223.
[9] 任小西,唐玲,张杰. 基于OpenMP多线程动态负载均衡技术研究[J]. 世界科技研究与发展,2008,30(3):281-285.
[10] 董俊,黄传河. 改进Dijkstra算法在GIS导航应用中最短路径搜索研究[J]. 计算机科学,2012,39(10):245-247,257.

