0 引言

    在计算机视觉领域中的一个重要研究方向是对运动目标的跟踪，而应用在运动目标跟踪方向的一种常用方法是Mean Shift算法，它是指通过均值漂逸^[1]的方法，从目标前一帧的真实位置逐步迭代至当前帧目标位置的过程。FUKUNAGA K等^[2]人在1975年最早提出了该算法，并由CHENG Y Z^[3]在1995年加入核函数后改进推广，之后被运用到运动目标的跟踪领域。

    Mean Shift算法以复杂度小、易于集成等优点在运动目标跟踪领域应用非常广泛。并且它采用核函数直方图模型，能够有效应对目标边缘被遮挡、目标的变形等问题。但是单一的Mean Shift算法也存在一些缺点，如在跟踪过程中，由于Mean Shift的核函数窗口大小是固定不变的，当目标尺寸变化时就会导致跟踪失败。文献[4]针对这一点提出了基于运动矢量分析的Mean Shift核窗宽动态更新模型，达到了一定的效果；COLLINS R T^[5]提出了一种Lindbeger图像多尺度理论，它在迭代过程中会不断计算DOG算子与核窗的卷积，计算量较大；文献[6]提出了三步法，即用正负10%的核窗口大小与原核窗进行3次搜索，并选择巴氏距离^[7]最小的为最佳核窗大小。3次的搜索大大增加了搜索时间，影响实时性，并且核窗口调整范围有限。彭宁嵩^[8]等提出用形心进行配准来检测角点的方法以及覃剑^[9]提出用边界力来约束Mean Shift核窗宽的算法，一定程度上缓解了目标变大带来的影响，但是算法仍然都比较复杂。文献[10]针对目标尺寸变化以及目标运动速度快和遮挡问题，提出一种结合光流场的自适应Mean Shift跟踪算法，提高了跟踪可靠性，但它局限于透视变化的先验基础上，仍然会出现诸多问题。文献[11]加权目标区域像素点空域后，利用Mean Shift算法搜索其彩色图像实现对快速运动目标的定位，再根据目标缩放因子实现对尺寸变化的目标的跟踪，大大提高了准确度，但是增加了计算量。文献[12]针对相似背景颜色干扰问题提出多特征自适应融合的Mean Shift目标跟踪方法，但是它的尺寸自适应效果并不理想，影响跟踪准确性。综合前人的方法以及问题，本文提出一种基于边缘特性的Mean Shift核窗口自动调节方法，它是检测目标区域的边缘，根据形心求取核窗口大小，核窗口大小会实时地根据目标的尺度变化而变化，提高跟踪准确度，并且算法复杂度大大减小。

1 Mean Shift跟踪技术

    Mean Shift算法运用在运动目标跟踪时，首先根据目标特征的概率直方图建立初始模板，一般选取目标的颜色特征，为了使跟踪效果更好，也会选择多种特征的结合；然后在当前帧中选择以前一帧的目标真实位置点为中心，以固定设置的Mean Shift搜索半径为半径的区域建立候选目标模板；再对两模板进行相似性度量。如果没满足预设要求，则以搜索到的新位置为起点继续搜索下一位置，直到满足预设的条件为止。

    令目标模板在前一帧的真实位置为y₀，在以当前帧对应位置y₀为中心的候选目标特征概率集合为{p_t(y)|t=1，…，d}，由于相邻两帧之间间隔很小，目标中心位移不会发生很大的跳跃性变化，所以y总是在y₀附近，则有巴氏系数ρ(y)在当前帧位置y₀的泰勒展开近似为：

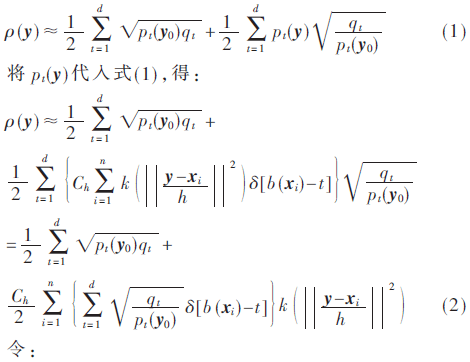
    按照这个方法反复搜索下去，直到Mean Shift向量满足||M_h，g(x)||<ε条件，ε为预先设定的允许误差阈值，这时就完成了从上一帧到当前帧的目标跟踪任务。连续不断地执行上一帧到当前帧的搜索，就完成了运动目标的连续跟踪。

2 Mean Shift核窗口自适应方法

    Mean Shift算法在运动目标跟踪领域得到了广泛的应用，但其固定的核窗口会导致跟踪准确度降低，甚至会导致跟踪失败。文中就这个问题提出了一种基于边缘特性的Mean Shift搜索核半径自适应目标的跟踪方法。

2.1 固定核窗口跟踪问题 

    视频画面中物体的运动方式各种各样，有的保持与摄像机的距离做各种速度的运动；有的可能远离摄像机运动；有的靠近摄像机运动。这3种情况下，目标会存在目标形状不变、变小、变大的情况。目标的大小改变以后，核窗口固定的Mean Shift搜索会影响到目标跟踪的准确度，甚至是跟丢目标。

    分析远离和靠近摄像头的情况如图1所示。图1(a)是在目标远离第1帧的跟踪情况，由于采用的核窗口大小与跟踪的目标大小基本吻合，所以定位跟踪效果准确。图1(b)是目标远离第300帧的跟踪情况，Mean Shift核搜索窗口大小没变，而跟踪的目标因远离或其他原因逐渐变小，当附近存在特征类似的物体噪声时，定位中心不准确，还能勉强跟踪到目标。可是当目标变得更小，而类似干扰物体却更加明显，这时的跟踪效果如图1(c)目标远离800帧所示，完全跟丢目标。这样的情况很有可能存在，比如在高速公路上，跟踪的目标车辆远离摄像机，类似干扰车辆迎面开来的情况。现又假设跟踪的目标是迎面靠近摄像机的情况，就会发生图1(d)～(f)的情况，为了能够分辨出搜索框，图1(f)的搜索框调成了黑色。目标越来越大会导致Mean Shift在搜索匹配时有很大的随机性，并且不能真实反映出完整的目标特征。可见，搜索的核窗口在Mean Shift算法中的重要性。所以寻求一种能自动调节核窗口大小的Mean Shift搜索算法是本节研究的重要内容。

2.2 以目标形心为中心的最小外“接”圆

    目标的最小外“接”圆的半径可认为是Mean Shift搜索算法的核半径，这里的外“接”圆的含义是指：无论目标是什么形状，都可以用一个最小的圆把它“圈”起来，如图2所示。

    但是以形心为圆点中心的外“接”圆才是Mean Shift搜索算法的最佳核半径，如图3所示。

    当运动的目标在Mean Shift算法的搜索窗口中心时，搜索的视觉效果与准确度是最佳的，且在保证目标特征都在搜索窗口内的情况下要使搜索半径越小越好，以减少外界的影响。由数学知识可知，在相同大小的钝角三角形中，图3(a)的外接圆的半径要比图3(b)以形心为中心的外“接”圆半径大，所以图3(b)的半径才是最佳的Mean Shift算法的搜索半径。

2.3 基于目标边缘特性的形心求解

    由上一小节得知，Mean Shift算法的最佳搜索半径应是以形心为中心的外“接”圆半径，那么本章算法在求此半径之前需先求出运动目标的形心位置。

    面的形心为截面图形的几何中心，这里的面不一定是完整的面，空心的面、甚至是出现缺口的面都能准确求解出其形心，如图4所示。

    所以不需要得到完整的目标形状就可以求出形心，由于边缘的特殊性，算法选择检测出运动目标的边缘，得到大致的轮廓，获取出边缘特性的二值图像，然后进行形心的求解。

    为了简单方便，算法不再求取整个图像帧的二值图像，而只需要在仅包含运动目标区域及其领域内边缘检测得到二值图像。由于目标可能与相似移动的物体接壤，所以这里要通过连通域分析及形态学处理后才能得到目标较准确的二值图像。 

    令(x₀，y₀)为目标模板在前一帧的真实中心位置，设{f(x，y)|x²+y²≤(1+10%)h}为以当前帧位置(x₀，y₀)为中心、(1+10%)h为半径区域内的二值图像集合，h为Mean Shift初次搜索的核窗口大小，该大小范围包含了前一帧运动目标模板的所有特征。算法把范围扩大是为了解决运动目标变大的情况。由于相邻两帧之间间隔很小，目标区域不会发生很大的跳跃性变化，所以扩大绰绰有余，由于：

2.4 自适应核窗口半径

    求出视频图像当前帧中运动目标的形心坐标以后，本文算法用一个包含目标所有轮廓的圆去一步一步地夹逼目标二值图像，从而得到以形心为中心的最小外“接”圆，进而得出其半径，这个半径就是更新后的Mean Shift搜索算法的核窗口半径，如图5所示。

    图5中初始大小的圆半径为(1+10%)h，二值图像中，易知在圆上的所有像素值为0，减小圆半径，当圆上的像素值首次大于0时，认定此时的圆为所求“夹”住目标的圆，此时的半径为所需要求出的半径，即为Mean Shift搜索算法的新核窗半径。

    令以形心(x_poid，y_poid)为中心的初始圆半径为h₀=(1+10%)h，h为Mean Shift初始搜索核半径，则该圆可表示为：

    设在圆上所有像素点的像素值为f(x，y)，那么求取新核窗半径的算法步骤为：

    (1)设初始圆半径为h₀=(1+10%)h，h为Mean Shift初始搜索核半径；

    (2)圆{(x-x_poid)²+(y-y_poid)²=[(1-j%)h₀]²|j=0，…，n}上的所有像素点为(x，y)，其中j为小于100的循环次数，这些像素点对应二值图像上的像素值为f(x，y)；

    (3)如果满足f(x，y)>0条件，则循环结束，此时得到新核窗半径为h_auto=(1-j%)h0，即h_auto=(1-j%)(1+10%)h，否则返回第(2)步继续循环。

    利用Mean Shift算法在当前帧进行搜索前，先通过以上步骤，根据当前帧目标边缘特性的二值图像，求得实时更新的搜索半径，再进行后面的搜索步骤，从而达到了Mean Shift可自动调节核窗大小的目的。

3 实验结果对比分析

    本实验在OpenCV3.0+VC++6.0+MATLAB平台上完成，实验主要验证文中所提出的Mean Shift核窗自动调节的跟踪算法的优点及跟踪效果。选取一段在广西大学大礼堂外的道路与同学合作拍摄的运动目标逐渐靠近摄像机的视频图像，当时多云天气，光线较好。视频中把测试者与电动车看成一个待跟踪的运动目标，测验者驾驶电动车，从远处逐步的向镜头开来，测试者与电动车这个目标逐渐的变大，甚至还从正面转到了侧面，最后从镜头的后边开出。实验结果如图6所示。

    图6(a)中圆圈表示固定核窗的Mean Shift算法跟踪效果，图6(b)中圆圈表示本文改进的可自动调节核窗大小的Mean Shift跟踪效果。对比可以看出，由于目标的迎面靠近会逐渐变大，固定跟踪的核窗口根本无法确定出目标的正确中心位置，并且不能包含全部的目标特征，会逐步遗失运动目标的特征；根据目标的变化情况而自动调节搜索核窗大小的新跟踪算法能够包含全部的目标特征，且能准确定位目标位置，对目标实施有效跟踪。

    为了使结果更具说服力，本文对图6中最后一幅图的跟踪效果进行详细分析，利用运动目标的二值图像来分析Mean Shift搜索核窗口所能够包含的真实运动目标的点，如图7所示。

    根据图7二值图像的特征点数，分析原始Mean Shift固定核窗口跟踪算法与文中新提出的基于边缘自适应的Mean Shift目标跟踪方法的搜索错误率σ、搜索准确率η以及目标信息完整度δ。搜索错误率表示在Mean Shift搜索过程中，搜索到的背景特征点与搜索总特征点的比率；搜索准确率表示在Mean Shift搜索过程中，搜索到的目标特征点与搜索总特征点的比率；搜索目标信息完整度表示搜索到的目标特征点与目标总特征点数的比率。搜索准确率和搜索目标信息完整度共同来表征对目标的跟踪准确度，对目标信息包含越完整跟踪的目标越准确，搜索的准确率越高，对目标特征的跟踪越高。

    经过处理后图像的分辨率是800×600，480 000个像素点。二值图像特征点中，令目标总特征点为M个，Mean Shift搜索窗口所包含像素点为N个(其中目标特征像素点有N₁个，背景特征像素点有N₂个)。则搜索错误率σ为：

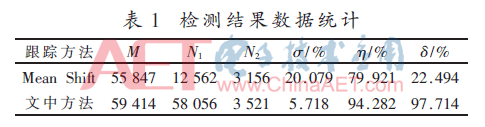
    把实验的数据统计在表1中，对其数据分析可以得出：

    (1)原有的Mean Shift固定搜索窗口算法搜索到的特征错误率有20.079%，而文中新提出的方法，即可自动调节的搜索核窗口虽然包含的背景错误特征点数略多于Mean Shift固定核窗算法，但其包含了大量的运动目标特征，特征错误率只有5.718%，从而使搜索准确率达到了94.282%；

    (2)Mean Shift算法固定搜索窗仅包含了22.494%的运动目标特征信息点，而文中算法高达97.714%的目标信息，进而使跟踪目标的准确度大大提高。

4 结束语

    文中提出了一种基于边缘自适应的Mean Shift目标跟踪方法，其思想是使Mean Shift搜索核窗口大小能够根据目标的形状变化而自动调节，利用目标二值图像边缘信息，找出其形心，通过逐步缩小的圆去夹逼目标，进而找出最适合的Mean Shift搜索核窗口。实验结果表明，该方法能够使Mean Shift搜索核窗口包含大量而完整的运动目标特征信息，降低搜索的错误率，提高搜索准确率，从而精确地跟踪运动目标。此方法虽然能够非常精确地跟踪运动目标，但当有其他类似运动物体与运动目标接壤时，求解目标领域内的二值图像就变得困难，从而会影响形心以及搜索核窗大小，这是今后要研究解决的问题。

参考文献

[1] 周芳芳，樊晓平，叶榛.均值飘逸算法的研究与应用[J].控制与决策，2007，22(8)：841-847.

[2] FUKUNAGA K，HOSTETLER L.The estimation of the gradient of a density function with applications in Pattern Recognition[J].IEEE Transactions on Information Theory，1975，21(1)：32-40.

[3] CHENG Y Z.Mean Shift, mode seeking, and clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1995，17(8)：790-799.

[4] 田纲.基于多特征融合的Mean Shift目标跟踪计算研究[D].武汉：武汉大学，2011.

[5] COLLLINS R T.Mean-shift blob tracking through scale space[C].In：Proc.Of the IEEE Conf. on Computer Vision and Pattern Recognition(CVPR’03)，2003：234-240.

[6] COMANICIU D，RAMESH V，MEER P.Kernel-Based object tracking[J].IEEE Trans.On Pattern Analysis and Machine Intelligence，2003，25(5)：564-575.

[7] 宣国荣，柴佩琪.基于巴氏距离的特征选择[J].模式识别与人工智能，1996，9（4）：324-329.

[8] 彭宁嵩，杨杰，刘志，等.Mean Shift跟踪算法中核函数窗宽的自动选取[J].软件学报，2005，16(9）：1542-1550.

[9] 覃剑.视频序列中的运动目标检测与跟踪研究[D].重庆：重庆大学，2008.

[10] 李剑峰，黄增喜，刘怡光.基于光流场估计的自适应Mean-Shift目标跟踪算法[J].光电子激光，2013，23（10）：1996-2002.

[11] 杨志菊，刘宝华.基于Mean Shift的变尺寸快速运动目标自适应跟踪算法[J].太赫兹科学与电子信息学报，2015，13(2)：240-244.

[12] 刘苗，黄朝兵.基于多特征自适应融合的Mean Shift目标跟踪方法[J].现代计算机（专业版），2016(4)：68-72.

作者信息:

周  杨，胡桂明，黄东芳

(广西大学 电气工程学院，广西 南宁530004)