基于自适应线性神经元网络的谐波检测算法-AET-电子技术应用

基于自适应线性神经元网络的谐波检测算法

2017年电子技术应用第6期

方树1，韩杨2，罗飞3，徐琳4

1.国网四川省电力公司，四川成都610041；2.电子科技大学，四川成都611731； 3.国网凉山供电公司，四川西昌615050；4.国网四川省电力公司电力科学研究院，四川成都610072

摘要： 为了克服基于傅里叶变换（FFT）谐波检测算法运算量大、实时性不强、易受噪声影响的缺点，提出了基于自适应线性神经元网络（ADALINE）的谐波检测算法，建立了基于最小二乘法（LMS）的最优解求解过程的数学模型，根据LMS误差与各次谐波傅里叶系数之间的三维流形的几何形状选择算法的步长因子。采用时域迭代的方法准确地提取基波有功、无功和各次谐波分量，为实现APF可选择性谐波补偿奠定了基础。

关键词： 谐波检测最小二乘法自适应线性神经元网络步长因子

中图分类号： TN911；TM46
文献标识码： A
DOI：10.16157/j.issn.0258-7998.2017.06.021
中文引用格式： 方树，韩杨，罗飞，等. 基于自适应线性神经元网络的谐波检测算法[J].电子技术应用，2017，43(6)：83-86.
英文引用格式： Fang Shu，Han Yang，Luo Fei，et al. A novel harmonic estimation algorithm based on adaptive linear neural network[J].Application of Electronic Technique，2017，43(6)：83-86.

A novel harmonic estimation algorithm based on adaptive linear neural network

Fang Shu1，Han Yang2，Luo Fei3，Xu Lin4

1.State Grid Sichuan Electric Power Company，Chengdu 610041，China； 2.University of Electronic Science and Technology of China，Chengdu 611731，China； 3.State Grid LiangShan Electric Power Supply Company，Xichang 615050，China； 4.State Grid Sichuan Electric Power Research Institute，Chengdu 610072，China

Abstract： To overcome the shortcomings of the conventional FFT-based harmonic estimation algorithms due to extensive computational load, poor real-time capabilities and poor noise immunities, a novel harmonic estimation algorithm based on adaptive linear neural network(ADALINE) is proposed. The mathematical model of the algorithm is presented using the least mean square(LMS) algorithm, and the step-size selection of the algorithm is discussed using three-dimensional manifold based on the LMS error and the Fourier series coefficients. The fundamental active, reactive component and the individual harmonic component are extracted from the load current using time-domain iterations, which lays the basis for the selective harmonic compensation purposes.

Key words : Harmonic detection；least mean square algorithm；ADALINE；step-size

0 引言

目前，谐波电流检测主要采用频域法和时域检测法。文献[1]提出基于快速傅里叶变换（FFT）的频域谐波检测方法，但容易出现频谱泄漏等诸多问题。文献[2]提出自适应谐波检测方法，该方法根据自适应干扰对消的原理，具有较高的检测精度，但是动态响应较慢。文献[3-5]提出采用人工神经网络的谐波检测算法，但该方法计算量大、实时性差。文献[6]提出基于神经网络的谐波辨识方法，描述了该方法的实现过程，但计算量很大。文献[7]采用神经网络控制器实现对谐波电压的抑制。文献[8]比较了时域与频域神经网络方法在有源滤波器中的应用。文献[9]采用神经网络实现谐波检测，并采用滑模变结构控制实现对谐波的补偿。文献[10]采用神经网络从负荷电流中提取3、5次谐波分量，该方法采用10个隐含层神经元，网络规模小，有较高的稳态精度。文献[11]提出提升小波变换和变步长LMS相结合的自适应谐波检测算法，对谐波电流进行正交变换，有效减少输入数据的互相关性，加快LMS的收敛速度，稳态误差较小。

1 基于自适应线性神经元网络的谐波检测算法模型

自适应线性神经元网络(Adaptive Linear Neural Network，ADALINE)算法是一种采用最小二乘（LMS）寻找最优解的优化数学方法，其原理图如1所示。

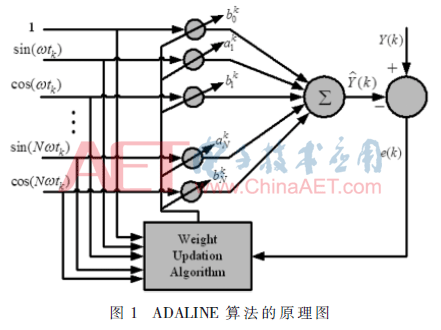
根据ADALINE的定义，任意信号Y(t)可表示为：

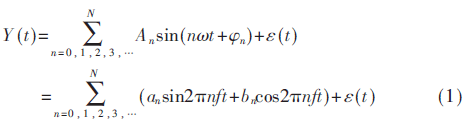
其中矩阵R为实对称阵。从式(6)看出，均方误差ε是关于权系数向量的二次函数，对ε求偏导得：

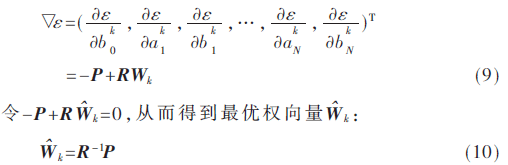
式（10）称为Weiner解，对应于权向量空间最优解的点，该点的目标函数取得最小值ε_min。采用这种方法计算最优权向量涉及到对矩阵求逆，当输入信号是谐波含量高的随机信号流时，难以实时计算准确的R^-1。因此，可对第k步平方误差ε_k直接求偏导得：

2 步长因子对谐波检测算法的影响

权系数向量的维数与估计的谐波次数有关。当估计的谐波次数远小于实际负载的谐波电流次数时，必然会引起较大的计算误差，反之又会引起计算量的增加。因此需要在两者之间进行折衷，同时权系数的精度也受到学习因子的影响，以下通过仿真进行分析。

不失一般性，设被检测的信号为：

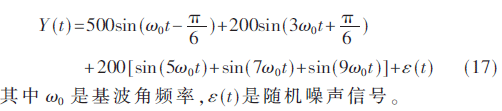
图2为在不同基波步长因子μ₁情况下，信号的基波幅值由500突变为1 000时，基波参数a₁sin(ω₀t)、b₁cos(ω₀t)和检测误差i_err的三维流形图，其中谐波步长因子μ_i=0.003 9（i=3，5，7，9）。图2表明，当μ₁=0.001 2时，三维流形的轨迹从i_err=0平面以500为半径的圆，基波幅值突增后，经过一系列的振荡，收敛到i_err=0平面以1 000为半径的圆；当μ₁=0.012，信号突变后i_err经过短暂的过渡过程收敛到i_err=0平面；当μ₁=0.12时，三维流形轨迹从初态到终态都严重地畸变。

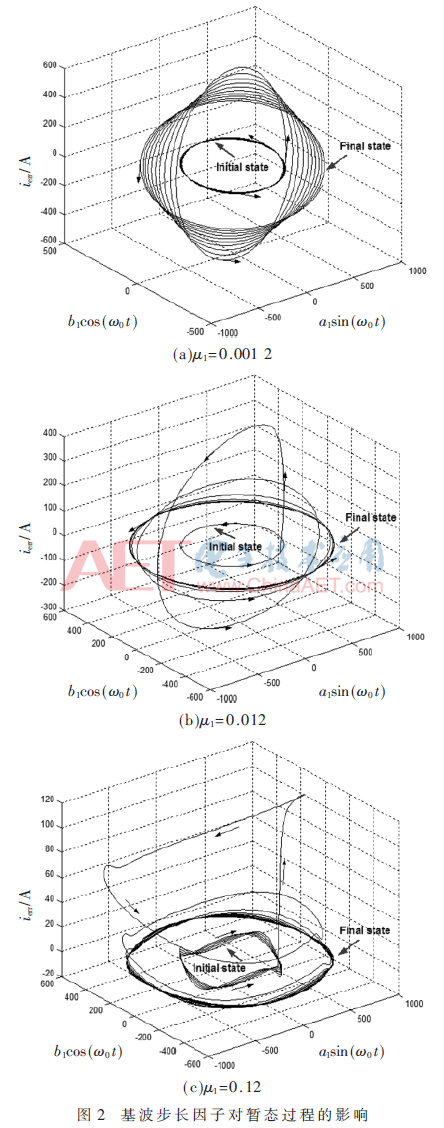
仿真结果表明，μ₁过小，尽管检测精度很高，但动态过程收敛缓慢；μ₁过大，又会引起检测值畸变严重，导致整个检测过程发散，系统失稳。因此μ₁需要在检测精度和动态响应速度两方面作折衷选择，其取值范围可以从三维流形的几何形状直观地看出。

3 基于CCS的算例分析

为了验证上述谐波检测算法的可行性，将该算法在浮点型DSP TMS320C6726硬件平台中通过编程实现。下面通过两个算例加以说明。图3、图4中横坐标表示采样点数，采样频率为10 kHz，纵坐标单位为A。

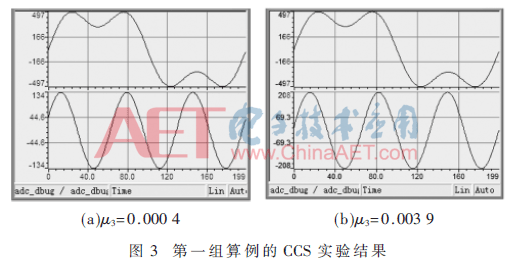
第一组算例中Y(t)=500sin(ω₀t)+200sin(3ω₀t)。图3分别给出了不同3次谐波步长因子μ₃下的采样电流和通过该检测算法重构的3次谐波波形，其中μ₃分别为0.000 4和0.003 9，基波因子μ₁均为0.012。当μ₃=0.000 4时，估计的3次谐波幅值为134 A，即3次谐波的估计误差达到33%，如图3(a)所示；当μ₃=0.003 9时，3次谐波幅值为208 A，误差减小至4%，如图3(b)所示。

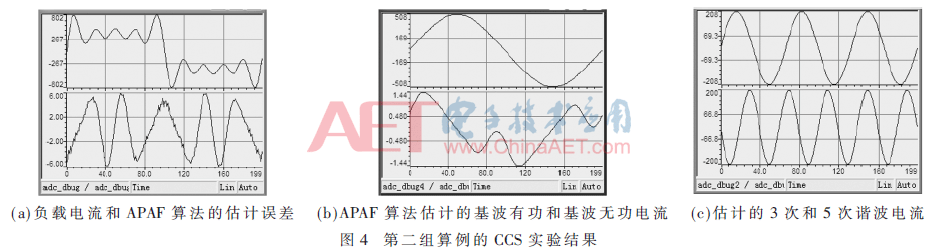
第二组算例中Y(t)=500sin(ω₀t)+200sin(3ω₀t)+200sin(5ω₀t)+sin(7ω₀t)+sin(9ω₀t)，其中μ₁=0.012、μ_i=0.003 9(i=3，5，7，9)。图4(a)为负载电流和APAF算法的估计误差波形图，其中估计误差在±6A之间波动，即估计误差在1%左右，确保了整个算法的收敛性；图4(b)为通过APAF算法重构的基波有功和基波无功电流分量，其中有功电流的估计误差为8 A(即1.6%)，而无功分量的估计误差为1.44 A(即0.28%)；图4(c)为APAF算法重构的3次、5次谐波分量结果，估计误差与图3非常类似，也就是说，步长因子在很大范围内是适用的，并不会随着负载电流谐波次数增加而改变。

算例分析结果表明，要实现快速准确地提取各次谐波分量，必须在考虑检测精度和动态响应速度两方面的前提下，合理地选择步长因子。

4 结论

基于自适应线性神经元网络ADALINE的谐波检测算法，能准确地提取基波有功、无功和各次谐波分量，克服了基于傅里叶变换（FFT）谐波检测算法运算量大、实时性不强、易受噪声影响的缺点，也避免了基于瞬时无功理论（IRPT）谐波检测算法易受电压畸变影响的不足，为实现APF可选择性谐波补偿奠定了基础。

参考文献

[1] 潘文，钱愈涛，周鹦.基于加窗插值FFT的电力谐波测量理论窗函数研究[J].电工技术学报，1994，9(1)：50-54.

[2] BARROS J，PEREZ E.An adaptive method for determining the reference compensating current in single-phase shunt active power filters[J].IEEE Transactions on Power Delivery，2003，18(4)：1578-1580.

[3] HAN B M，BAE B Y，OVASKA S J.Reference signal generator for active power filters using improved adaptive predictive filter[J].IEEE Transactions on Industrial Electronics，2005，52(2)：576-584.

[4] RUKONUZZAMAN M，UEMATSU T，NISHIDA K，et al.Harmonic and reactive currents estimation with adaptive neural network and their compensation with DSP control in single-phase shunt active power filter[C].Telecommunications Energy Conference，2003：358-365.

[5] RUKONUZZAMAN M，NAKAOKA M.Adaptive neural network based harmonic current compensation in active power filter[C].International Joint Conference on Neural Networks，2001，3：2281-2286.

[6] OSOWSKI S.Neural network for estimation of harmonic components in a power system[J].IEE Proc.C，Gener.Transm.Distrib.，1992，139(2)：129-135.

[7] KUMAMOTO A，HIKIHARA T，HIRANE Y，et al.Suppression of harmonic voltage distortion by neural network controller[C].Proc.IEEE Ind.Appl.Annual Meeting，Houston，Texas，USA，1992：754-761.

[8] ROUND S，MOHAN N.Comparison of frequency and time domain neural network controllers for an active power filter[C].Proc.IEEE IECON，Maui，Hawaii，USA，1993：1099-1104.

[9] KANDIL M，ABDELKADER S，ELMITWALLY A，et al.A novel three-phase active filter based on neural networks and sliding mode control[C].Proc.IEEE Industrial Elec.Conf.(IECON)，San Jose，California，USA，1999：867-872.

[10] PECHARANIN N,MITSUI H.Harmonic detection using neural network[C].Proc.IEEE Intl.Conf.On Neural Networks，Perth，Australia，1995：923-926.

[11] 高红霞，刘晓乐.电力谐波检测改进算法在DSP上的应用与实现[J].电子技术应用，2015，41(4)：125-128.

作者信息：

方树1，韩杨2，罗飞3，徐琳4

(1.国网四川省电力公司，四川成都610041；2.电子科技大学，四川成都611731；

3.国网凉山供电公司，四川西昌615050；4.国网四川省电力公司电力科学研究院，四川成都610072)

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容