简彩仁1，吕书龙2

　　(1.厦门大学 嘉庚学院,福建 漳州 363150; 2.福州大学 数学与计算机科学学院,福建 福州 350108)

　　摘要：基于表示理论的子空间分割方法有着广泛的应用。经典的子空间分割方法通过不同的正则项求解仿射矩阵，而忽略了特征属性对子空间分割的影响。针对这些问题，通过特征权重自适应的思想对最小二乘回归子空间分割方法进行改进，提出权自适应最小二乘回归子空间分割方法。在6个数据集上的实验结果表明该方法是有效的。

　　关键词：聚类；最小二乘回归；权自适应 ；子空间分割

　　中图分类号：TP311, TP371文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.10.016

　　引用格式：简彩仁，吕书龙.权自适应最小二乘回归子空间分割法［J］.微型机与应用，2017,36（10）：54-57,60.

0引言

　　*基金项目：福建省中青年教师教育科研社科A类项目（JAS151395）; 福州大学第九批高等教育教学改革工程项目（52001024）

　　子空间分割方法是近年来聚类方法研究的热点问题［17］，其目标是将数据集分割（或聚集）成几个簇，并使每一个簇对应于一个子空间。子空间分割方法已经成功应用在机器学习和计算机视觉等相关研究中。现实中的数据近乎可以视为是混合子空间，因此子空间分割方法在图像聚类、图像分割、运动物体识别和基因表达数据识别等领域有着广泛的应用［16］。

　　子空间分割方法［3］用数学语言可以描述为：给定k个子空间{Si}ki=1采样的数据向量集合X=［X1,…,Xk］=［x1,…,xn］∈Rm×n，其中Xi是从子空间Si中采样的ni个数据向量的集合，n=∑ki=1ni。子空间分割方法根据它们采样的基子空间分割数据。

　　子空间分割方法是一种重要的聚类方法，在过去的二十几年里，已经提出许多经典的子空间分割方法。根据其表示方式的不同子空间分割方法可以粗略地分为四类［3］：代数方法、迭代方法、统计方法、谱聚类方法。

　　基于谱聚类的子空间分割方法在于求解仿射矩阵Z=(Zij)n×n，其中Zij用来度量两个样本xi和xj的相似度。理想的仿射矩阵是块对角的，不同类的两个样本的仿射矩阵值Zij=0，这样就便于利用谱聚类分割仿射矩阵，从而达到子空间分割的目的。以距离为背景的度量是一种最常见的相似度计算方法，例如Zij=exp(－xi－xj/σ),σ>0，然而这些方法仅仅考虑了样本两两之间的相似度而不能很好地刻画数据的本质特征。得益于样本表示理论，基于谱聚类的子空间分割方法得到了很好的发展，例如低秩表示子空间分割方法［2］、最小二乘回归子空间分割方法［3］和图正则化子空间分割方法［5］提出了一些新的计算仿射矩阵的方法，这些方法通过表示理论来得到相似系数。

　　低秩表示子空间分割方法旨在通过秩最小化来构建相似矩阵，最小二乘回归子空间分割方法通过F范数正则化达到内聚度，图正则化子空间分割方法通过拉普拉斯图正则化保持相似度。但是现实数据存在各类噪声，因此样本重构时，很容易受到噪声的影响，然而这些方法都忽略了样本重构时特征属性噪声对子空间分割的影响。为了弥补这一不足，利用特征属性加权的方法改进最小二乘回归子空间分割方法，并通过对特征权重进行非负限制达到自适应选择特征权重的目的。该方法可以实现自适应选择特征权重，并保持最小二乘回归子空间分割方法的聚集性。

1相关研究

　　基于表示理论的子空间分割方法是近年来的研究热点，最小二乘回归子空间分割方法将经典的岭回归模型应用到子空间分割方法，文献［3］证明了该方法有很好的内聚性能。最小二乘回归子空间分割方法将每个样本点xi表示为其他样本点的线性组合xi=∑j≠iZijxj，并通过正则Z的F范数达到样本聚集的效果，最后用(Zij+Zji)/2表示xi和xj之间的相似度。

　　针对理想的无噪声数据集，最小二乘回归子空间分割方法为:

　　minZZFs.t.X=XZ

　　然而现实数据总是存在噪声，将该模型扩展为:

　　minZX－XZ2F+λZ2F

　　这是经典的岭回归模型，其解析解为Z*=(XTX+λI)－1XTX，其中，λ>0是正则参数，I是单位矩阵。

　　最小二乘回归子空间分割方法有很好的聚集性能，并且该方法有解析解，可以快速得到表示系数，然而它忽略了特征属性噪声对子空间分割的影响。

2权自适应最小二乘回归子空间分割

　　最小二乘回归子空间分割方法用X=XZ来重构样本，然而现实数据的特征属性总是存在噪声，但是最小二乘回归子空间分割方法没有考虑特征属性噪声对子空间分割的影响。针对这一不足，提出权自适应最小二乘回归子空间分割方法，该方法可以自适应地选择特征的权重，而不改变最小二乘回归子空间分割方法的聚集性能。

　　2.1目标函数

　　给定一个样本x=［x1,x2,…,xm］Τ∈Rm，由于现实数据在采样过程中存在噪声的影响，每个特征对模式识别方法的影响程度是不一样的，因此每个特征属性有不一样的权重，通过非负特征权重w=［w1,w2,…,wm］Τ∈Rm+的作用得到新的样本x~=［w1x1,w2x2,…,wmxm］Τ=diag(w)x，其中，diag(w)是一个m×m的以w为主对角线元素的对角矩阵，为达到特征权自适应的目的,限制∑mi=1wi=1,wi≥0,i=1,2,…,m。

　　因此，原始数据集X可以变为新的数据集diag(w)X，对其应用最小二乘回归子空间分割方法得到权自适应最小二乘回归子空间分割模型：

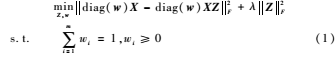
　　其中，λ>0是给定的正则参数。式（1）的第一项是加权重构项，其中参数wi表示第i个特征的重要程度，从而可以优化特征属性，使该方法更利于子空间分割；第二项是正则F范数，用以实现子空间分割的聚集性。

　　2.2目标优化

　　目标函数有两个参数w和Z，采用交替优化的方法实现问题（1）的求解。

　　（1）固定Z，优化w

　　固定参数Z，并且将无关的正则项去掉，式（1）变为：

　　下面的定理给出了求解方法。

　　（2）固定w，优化Z

　　固定w，并令X~=diag(w)X，则式（2）变为：

　　minZX~－X~Z2F+λZ2F（5）

　　令L(Z)=X~－X~Z2F+λZ2F，并将其展开：

　　L(Z)=Tr(X~TX~)+Tr(ZTX~TX~Z)－Tr(X~TX~Z)－Tr(ZTX~TX~)+λTr(ZTZ)

　　关于Z求导，并令其为0：

　　2X~TX~Z－2X~TX~+2λZ=0

　　从而得到解析解：

　　Z*=X~TX~+λI－1X~TX~（6）

　　其中，X~=diag(w)X，λ>0是正则参数，I是单位矩阵。

　　上述两个步骤都可以得到极小值，因此算法的收敛性可以得到保证，通过上述两个步骤的交替迭代过程可以得到式（2）的解。

　　2.3权自适应最小二乘回归子空间分割方法的聚集性质

　　最小二乘回归子空间分割方法有缩小相关数据系数和聚集性质［3］。定理2证明了权自适应最小二乘回归子空间分割方法也有这样的性质。

　　定理2给定一个向量y∈Rm，矩阵X∈Rm×n和参数λ>0，假设X已经按列标准化，z*是如下权自适应最小二乘回归子空间分割问题的解：

　　其中r=xTixj是样本相关系数。

　　证明：令L(z)=diag(w)y－diag(w)Xz22+λz22，由于z*是式（7）的解，必然有：

　　L(z*)zk=0

　　因此有：

　　－2xTidiag(w)(y－Xz*)+2λz*i=0

　　－2xTjdiag(w)(y－Xz*)+2λz*j=0

　　以上两式相减有：

　　z*i－z*j=1λ(xTi－xTj)diag(w)(y－Xz*)

　　X已经按列标准化，xi－xj2=2(1－r)，其中r=xTixj是样本相关系数。由于z*是式（7）的最优解，有：

　　diag(w)y－diag(w)Xz*22+λz*22=L(z*)≤L(0)=diag(w)y22（8）

　　因此diag(w)y－diag(w)Xz*2≤diag(w)y2，那么式（8）蕴含着：

　　z*i－z*j2y2≤1λ2(1－r)

　　定理2证明的权自适应最小二乘回归子空间分割方法的聚集能力表明模型的最优解是相关依赖的。假如xi和xj是高度相关的，即r=1，定理2表明xi和xj对应的表示系数zi和zj的不同程度为0，这样xi和xj就会聚成相同的簇。

　　2.4权自适应最小二乘回归子空间分割算法

　　类似于经典的基于表示理论的子空间分割方法，权自适应最小二乘回归子空间分割法（Adaptive Weight Least Square Regression Subspace Segmentation，ALSR）也是一种基于谱聚类的子空间分割方法，首先通过2.2节的方法解决式（2），得到该问题的解Z*，接着应用标准分割方法（Normalized Cuts）［8］对仿射矩阵(Z*+(Z*)T)/2进行分割。ALSR的计算步骤如下:

　　算法：权自适应最小二乘回归子空间分割算法（ALSR）

　　Input：数据矩阵X，正则参数λ，类数k

　　Output：k个类簇

　　(1)利用2.2小节的方法解决式（2），求得Z*：

　　①固定Z，利用式（4）优化w；

　　②固定w，利用式（6）优化Z；

　　直到收敛；

　　(2)计算矩阵 (Z*+(Z*)T)/2；

　　(3)应用标准分割方法将数据分成k个子空间。

3实验

　　为验证权自适应最小二乘回归子空间分割方法（ALSR）的有效性，与经典的子空间分割方法最小二乘回归子空间分割方法（LSR）［3］、图正则化子空间分割方法（GRSS）［5］、低秩表示子空间分割方法（LRR）［2］以及传统的聚类方法K均值（Kmeans）从聚类的准确率的角度进行比较。聚类准确率的计算公式［9］如下：

　　对一个给定的样本，令ri和si分别为聚类算法得到的类标签和样本自带的类标签，那么准确率的计算公式为：

　　其中，n为样本总数；δ(x,y)是一个函数，当x=y时，值为1，否则为0；map(ri)是一个正交函数，将每一个类标签ri映射成与样本自带的类标签等价的类标签。

　　3.1数据集

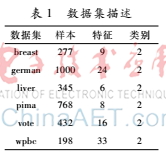
　　本文选用6个来自UCI数据库的常用于模式识别研究的公开数据集breast、german、liver、pima、vote和wpbc为研究对象，表1简要给出了它们的相关信息，更多的数据集描述可以参考UCI数据库的说明。

　　3.2实验结果与分析

　　本文的实验环境为Windows 7系统，内存2 GB，所有

　　方法都用MATLAB 2011b编程实现。实验结果用聚类准确率进行比较。实验中子空间分割方法ALSR、LSR、GRSS和LRR的正则参数设置为0.000 1，0.001，0.01，0.1，1，2，3，4，5，10。实验过程中遍历这些参数，实验结果选取平均聚类准确率最高的参数。GRSS的近邻数量固定为5。

　　为避免随机性，每种方法运行10次取聚类准确率的平均值。表2以聚类准确率的均值±标准差(P值)的形式给出实验结果。

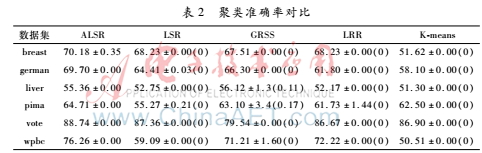
　　由实验结果得出以下结论：

　　（1）权自适应最小二乘回归子空间分割方法（ALSR）的聚类效果是理想的，除了在liver数据集上都取得最好的聚类准确率。其中，在liver数据集上聚类准确率不如图正则化子空间分割方法（GRSS），但是P值大于0.05，显示两者的聚类准确率相差不大。

　　（2）与经典的最小二乘回归子空间分割方法（LSR）对比，ALSR的聚类准确率显著高于LSR。这一结果说明考虑特征权重对于改进LSR是有效的。此外，与其他经典的子空间分割方法GRSS和LRR对比，ALSR方法也有较理想的聚类准确率。因此，ALSR是一种有效的子空间分割方法。

　　（3）与传统的K均值聚类方法（Kmeans）相比，ALSR在所有测试数据集上都可以取得更好的聚类准确率。尽管Kmeans聚类方法在某些数据集上有突出的聚类准确率，比如在vote数据集上可以达到86.90%的准确率，但是在其他数据集上聚类结果一般。因此，ALSR的聚类准确率比Kmeans聚类方法更突出。

　　3.3参数选择

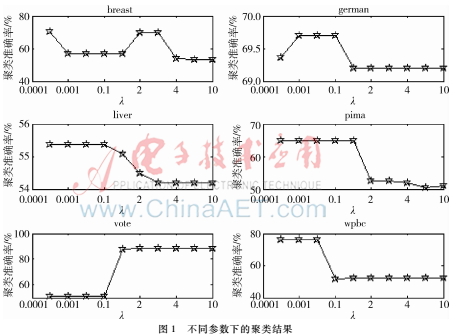
　　与LSR对比，ALSR通过自适应加权并没有增加新的参数，和LSR一样，ALSR只有一个参数：正则系数λ。图1的结果反映了正则参数λ对聚类准确率的影响。

　　从整体来看，聚类准确率对不同的正则参数λ较为敏感。但是从局部来看，ALSR的聚类准确率对不同的正则参数λ是相对稳定的，除了在vote数据集上，较小的正则参数λ具有较高的聚类准确率，这和文献［3］的研究结论是一致的。

4结论

　　本文用权自适应的思想对最小二乘回归子空间分割方法进行改进，提出权自适应最小二乘回归子空间分割方法。在6个数据集上的实验结果表明权自适应最小二乘回归子空间分割方法通过考虑不同特征权重对数据集的影响，可以得到较为理想的聚类准确率。如何降低正则参数λ对聚类准确率的影响将是对ALSR进行进一步研究的一个方向。

　　参考文献

　　［1］ ELHAMIFAR E, VIDAL R. Sparse subspace clustering［C］.Proceedings of 23rd IEEE Conference on Computer Vision and Pattern Recognition. Bonn, Germany, 2009: 2790-2797.

　　［2］ Liu Guangcan, Lin Zhouchen, Yu Yong. Robust subspace segmentation by low

　　rank representation［C］.Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 2010: 663-670.

　　［3］ Lu Canyi, Min Hai, Zhao Zhongqiu, et al. Robust and efficient subspace segmentation via least squares regression［C］.Proceedings of the 12th European Conference on Computer Vision, Firenze, Italy, 2012: 347-360.

　　［4］ 简彩仁, 陈晓云. 基于投影最小二乘回归子空间分割的基因表达数据聚类［J］. 模式识别与人工智能, 2015,28(8):728-734.