0 引言

    空间咨询数据委员会(CCSDS)推荐7/8码率LDPC码^[1]作为近地空间通信信道编码方案^[2-5]。这种LDPC码可以提供非常低的误码平台和较快的译码收敛速度^[6-8]，非常适合空间通信应用场景。7/8码率LDPC码串行编码的结构^[9-12]符合LDPC码线性分组码的特点，具有编码结构简单、编码速率快和编码器占用逻辑资源较少等优点。但是，随着空间通信要求的提高，串行编码的编码速率提升受到限制。

    本文提出一种低并行度高速编码结构设计。该编码结构通过合理的插“0”和改变生成矩阵结构，实现高速低并行度编码。

1 CCSDS标准LDPC编码原理

1.1 编码的数学原理

    LDPC的编码本质为矩阵的乘法运算。以（8 176，7 154）码[2]为例，输入7 154位待编码信息位，编码产生1 022位奇偶校验位，编码输出为8 176位系统码。

    待编码的信息位数据为长度为7 154的信息向量n：

    矩阵G分为两部分，左边是7 154×7 154的单位矩阵，其中I为511×511的单位子矩阵，0是511×511的零矩阵；右边是矩阵B_i，j(i=1，2…14；i=1，2)，B_i，j是511×511的循环矩阵。矩阵的左边部分用于生成7 154位信息码，右边部分用于生成1 022位校验码。

    编码生成的系统码向量N：

其中b_i，j为循环矩阵B_i，j的第一行。这样，在采用可编程逻辑器件实现编码器时，只需要保存28个循环子矩阵B_i，j各自的第一行数据b_i，j(i=1，2…14；j=1，2)即可，减少硬件资源使用。

1.2 编码器的结构设计原理

    图1为串行编码器结构设计原理图。为了适应循环编码，将待编码的信息向量n分割为14个向量n=(p₁  p₂  …  p₁₄)，且：

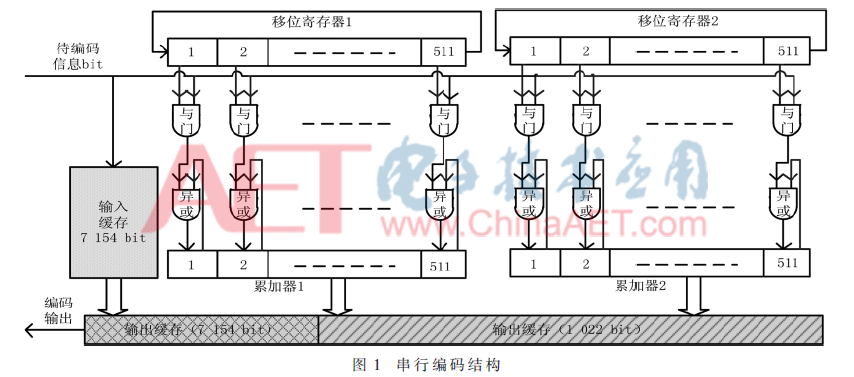
    编码过程如下：

    (1)初始时刻，循环移位寄存器1中存储的数据为b_1，1，循环移位寄存器2中存储的数据是b_1，2。累加器1中为511位0，累加器2中为511位0。

    同理，第2～511个时钟周期内，每个时钟周期循环移位寄存器1和2循环右移1位，对输入信息位重复第1个时钟周期相似的过程。511个时钟周期后，第一组循环校验矩阵结束。然后将循环移位寄存器1中数据b₁，1更换为b_2，1，循环移位寄存器2中数据b_1，2更换为b_2，2。

    (3)对输入的p₂，p₃，…，p₁₄向量，重复与p₁输入的处理相同的过程。当所有的7 154位待编码数据全部处理完毕，将输入的7 154位待编码数据和编码得到的累加器1、累加器2的数据组合为8 176位系统码，即最后得到的编码数据帧。

2 串行编码实现及存在的问题

    CCSDS给出的7/8LDPC码的编码帧格式^[3]为32+7 136+1 022+2 bit，为了保证编码的输入和输出同步，在待编码数据输入编码器之前，待编码数据转变为7 136位待编码数据+1 056位“0”，在编码器的校验矩阵B_i，j中添加第16、17组全“0”的校验循环矩阵。这样使得编码输入和输出数据位数完全一致，有利于编码器设计结构的简化。编码结构中插“0”结构如图2。

    串行编码器结构简单，占用资源少，但是存在不足之处：采用串行输入的方式，编码能够达到的最大速率有限，对于有图像数据传输的应用场合，显示出局限性。

3 低并行度编码结构设计

3.1 低并行度编码的数学原理

    本文根据7/8 LDPC码编码矩阵的特点提出了低并行度编码的数学原理。假设输入的待编码数据为7 154位的向量n，且有n=(n₁  n₂  …  n₇₁₅₄)，将向量n分割为14个长度511向量p_i(i=1，2，…，14)。为了使输入的待编码信息位符合奇偶位并行输入的特点，对14个信息位向量p_i(i=1，2，…，14)进行“0”位填充，使待编码信息变为7 168位的向量m，且有m=(k₁  k₂  …  k₁₄)，其中k_i(i=1，2，…，14)为长度512的向量。如下：

    设待编码信息位向量k拆分为奇位向量和偶位向量：奇位向量odd_k=(n₁  n₃  …  n₅₀9  n₅₁₁)，偶位向量even_k=(n₂  n₄  …  n₅₁₀  0)。

    将生成矩阵G的右边部分的两列B_i，j(i=1，2，…，14；j=1，2)循环子矩阵拆分成与奇编码矩阵odd_B_i，j和偶编码矩阵even_B_i，j，如下：

    所以可得编码校验位向量：

3.2 编码结构设计

    图3为低并行度编码器结构框图。根据低并行度编码数学原理，在编码之前先对数据每隔511位插入1个“0”，在插满14个“0”之后，在编码数据后补齐1 042个“0”，使待编码数据帧长度为8 192 bit。低并行度并行编码采用4个循环移位寄存器。编码过程如下：

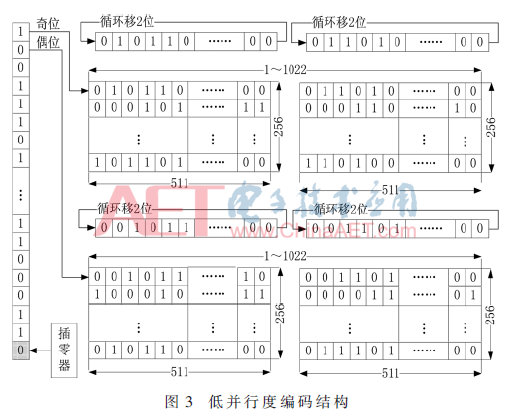
    (3)对于输入向量k₂，k₃，…k₁₄，重复与k1输入的处理相同的过程。当所有7 154位待编码数据全部处理完毕，将输入的7 154位待编码数据和编码得到的累加器1，累加器2的数据组合为8 176位系统码就是编码数据帧。

4 编码性能和编码效率分析

    定义衡量编码性能的公式如下：

5 结论

    本文提出的低并行度7/8码率LDPC编码是在CCSDS标准提出的串行编码结构上采用插“0”设计和改变生成矩阵的形式，设计新的编码结构，大幅度提升了编码速率和编码效率，扩展了LDPC编码的应用范围，具有创新性。另外，该低并行编码的并行度可以根据设计需求改变，对于工程应用有较好的适应性。

参考文献

[1] GALLAGER R G.Low-density parity-check codes[J].IRE Transactions on Information Theory，1962，8(1)：21-28.

[2] CCSDS.CCSDS 131.1-O-2-low density parity check codes for use in near-earth and deep space applications[R].Washington，DC，USA，2007.

[3] CCSDS.CCSDS 131.0-B-2-TM synchronization and channel coding[S].Washington，DC，USA，2011.

[4] CCSDS.CCSDS 230.2-G-1-next generation uplink[R].Washington，DC，USA，2014.

[5] CCSDS.CCSDS 231.1-O-1-short block length LDPC codes for TC synchronization and channel coding[R].Washington，DC，USA，2015.

[6] MACKAY D C.Good error-correcting codes based on very sparse matrices[J].IEEE Transactions on Information Theory，1999，45(2)：399-431.

[7] Lin Shu，Chen Lei，Xu Jun.Near shannon limit quasicyclic low-density parity-check codes[J].IEEE Transaction on Communication，2004，52(7)：1038-1042.

[8] 袁东风，张海刚.LDPC码理论与应用[M].北京：人民邮电出版社，2008：20-25.

[9] 燕威，薛长斌.高效低功耗低并行度LDPC编码方法[J].电子与信息学报，2016，38(9)：2268-2273.

[10] Sun Yang，KARKOOTI M，CAVALLARO J R.Vlsi decoder architecture for high throughput and variable block-size and multi-rate ldpc codes[C].IEEE International Symposium on Circuits and Systems，2007：2104-2107.

[11] CHENG L，LI G X，ZHU H P，et al.LDPC encoder design and FPGA implementation in deep space communication[C].Proceedings of the International Conference on Logistics，Engineering，Management and Computer Science，Paris，2014，101：343-346.

[12] 刘冬培，刘衡竹，张波涛.基于准循环双对角阵的LDPC编码算法研究[J].国防科技大学学报，2014(2)：156-160.

作者信息：

燕  威1，2，朱  岩1

（1.中国科学院国家空间科学中心，北京100190；2.中国科学院大学，北京100190）