0 引言

    随着现代生活节奏的逐步加快，人们生活压力的不断加大，由睡眠问题引起的疾病越来越多，所以基于交叉学科发展起来的睡眠医学，得到了很多医学研究机构以及高校的关注，致力于了解机体睡眠过程并解决睡眠功能障碍^[1]。目前，在睡眠医学领域内有人工睡眠分期和自动睡眠分期两种方法来分析睡眠过程，人工睡眠分期方法需要专家亲临现场分析，该方法会因为客观原因以及专家主观原因导致误判率高。自动睡眠分期方法是目前睡眠医学领域内主要的睡眠分析方法，该方法需要建立算法处理模型，对睡眠过程进行有效的特征提取和分类，常用的方法有样本熵（Sample Entropy，SE）^[2]、Hilbert-huang变换（HHT）^[3]、离散小波变换（Discrete Wavelet Transform，DWT）^[4]等，但是SE运行速度较慢，不适合大量数据的处理；HHT存在端点效应、模态混叠；DWT无法提取信号的非线性特征等问题。所以本文提出使用多尺度熵（Multi-scale Entropy，MSE）和主成分分析（Principe Component Analysis，PCA）的复合算法进行特征提取和降维，并在此基础上采用反馈神经网络（Back Propagation Neural Network，BPNN）实现对EEG睡眠状态的非线性映射和高分期准确率，同时，多尺度熵和主成分分析融合方法也是首次应用到自动睡眠分期领域，为自动睡眠分期提供了新的思路。

1 材料与方法

1.1 数据的获取和预处理

    仿真数据来自MIT-BIH生理信息库中Sleep-EDF的8组脑电（Electroencephalogram，EEG）实测数据，其中4组健康志愿者的睡眠数据（sc4002e0，sc4012e0，sc4102e0，sc4112e0），另外4组是有轻微失眠志愿者的睡眠数据（st7022j0，st7052j0，st7121j0，st7132j0），均采用Fpz-Cz导联方式。受试者包括男性和女性，年龄在21~35岁，未使用任何药物干扰，采样率均为100 Hz。数据库中每30 s EEG信号的睡眠分期结果已由经验丰富的睡眠专家人工标注^[5]。

    本文首先使用小波滤波方法实现对原始EEG信号去噪，根据EEG频率范围0.5~40 Hz，采用db4小波基和分解层数为8的自适应小波滤波。滤波完成后根据专家的分期结果将睡眠EEG数据（30 s）分为清醒期（Awake）、浅睡期（Light Sleep，LS）、深睡期（或慢波睡眠期Slow Wave Sleep，SWS）和快速眼动期（Rapid eyes movement，REM）共4个集合，为模式分类提供先验知识^[6]。

1.2 多尺度熵

    多尺度熵（MSE）是基于样本熵（SE）在不同尺度下的非线性分析方法，它能够描述信号在不同尺度下的复杂度和相关性^[7]。在睡眠分期特征提取中，通过计算EEG不同尺度的熵值来反映不同睡眠期之间的非线性特征。

    假设数据样本为N的某一离散时间序列{X_i}={x₁，x₂，…，x_N}，嵌入维数m和相似容限r（根据MSE的应用研究，在实验中优先选择m=2，r=0.15SD^[8]），原始数据的样本熵为：

1.3 PCA降维

    上述方法中采集到的多尺度熵值为睡眠期（30 s睡眠数据）在增加单位尺度的样本熵值，即一个维数。而EEG信号中包含大量的睡眠期，当增加过多尺度时，MSE维度过高将导致睡眠期的自动识别和运行速度上存在较大难度，因此本文采用主成分分析法（PCA）对MSE特征进行降维处理。

    PCA作为一种多元统计分析技术，首先对数据去相关，根据方差最大化原理，通过正交变换将原变量转换为一组线性不相关的主成分变量，压缩变量个数，最大化保存有效信息的同时剔除冗余信息，实现对数据的降维，一般主成分的选取标准是累计贡献率达到80%以上^[9-10]。

1.4 分类算法

    反馈神经网络（BPNN）的基本思想是根据最速下降法，对网络权值和阈值的不断调整，得到最小的网络误差平方和实现反向传播。在分类模型中，BPNN将PCA所包含主要信息的主成分作为输入参数，通过BP算法训练和实现对4种睡眠期的自动识别分类。

    BPNN的节点输出为：

    式(1)中x_i是节点输入，w_ij为输入节点j至隐含层节点i的连接权值，θ_j是隐含层节点的阈值，f是激活函数，一般选用Sigmoid函数，y_j是隐含层节点的输出，其结果为4种睡眠状态。

2 实验结果

2.1 多尺度熵结果

    序列的熵指数可以表征序列的复杂程度^[9]，图1为样本（sc4002e0，sc4012e0，st7022j0，st7052j0）的Awake、LS、SWS和REM四种睡眠期的多尺度熵值曲线，其结果在整体趋势上区别相对明显。同时，在相同尺度下，Awake、REM、LS、SWS的熵值逐渐递减，说明睡眠程度的加深与脑电信号的复杂程度呈负相关的变化趋势，其在特定尺度t下的主要统计分布如图2所示。图2显示出4种尺度下睡眠期的统计分布与MSE的结果保持一致，并且睡眠阶段之间存在显著性差异，因此多尺度熵可以区分四种不同的睡眠阶段。根据统计结果，为了不丢失信号的有效成分，采用尺度1-13的MSE值表征脑电EEG不同睡眠期的主要非线性动力学特征。

2.2 PCA降维结果

    为实现进一步对四种睡眠期的识别分类，采用PCA对MSE特征进行降维分析^[11]。通过MSE方法对EEG信号进行非线性特征提取，得到13个尺度下Awake、LS、SWS和REM的熵值特征，利用PCA对该特征进行降维，保证降低数据冗余的同时保留绝大多数EEG非线性特征，各成分所对应的累计贡献率如图3所示。

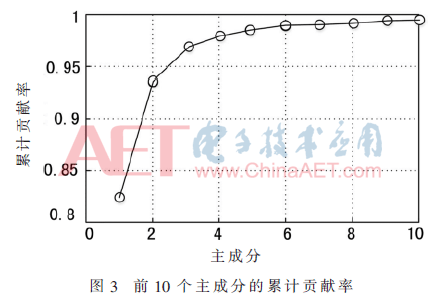
    由图3可知PCA前两个主成分的累计贡献率达到93.1%，表明它们已经包含了原变量的主要信息。因而选用PCA的前两个向量作为新的特征向量，代替原变量13个尺度的MSE特征，实现特征降维。

    当利用前2个主成分向量取代MSE特征，测试集样本为sc4002e0，sc4012e0，st7022j0，st7052j0的60组熵值特征，其中包含Awake、LS、SWS和REM各15组，PCA降维后的前2个主成分得分图如图4所示^[10]。图4显示四种睡眠阶段的熵值特征分布区域较为明显，说明通过前两个主成分已可以完全区分四种睡眠状态。

2.3 BPNN分类结果

    将受试者的1500个测试睡眠期输入已训练的BPNN分类模型，自动睡眠分期与专家人工分期的对比如图5所示，其结果的详细数据如表1。其中，专家分期结果在数据库中已由临床经验丰富的专家人工识别分类标注，该结果可以作为自动睡眠分期模型的性能评测依据。

3 讨论

    本研究通过MSE算法提取EEG信号的非线性动力学特征，利用PCA降维和BPNN分类，建立一种有效的自动睡眠分期方法。在表1中显示出本文模型相对于专家人工分期结果，自动分期模型Awake、LS、SWS和REM的识别准确率均在85%以上，平均准确率为87.9%，相比同类研究，达到较高的分期准确率。通过与专家分期结果的一致性检测，模型的kappa系数保持在了0.77，表明本文方法的自动分期结果相对于专家分期结果已达到高度的一致性，系统鲁棒性强。

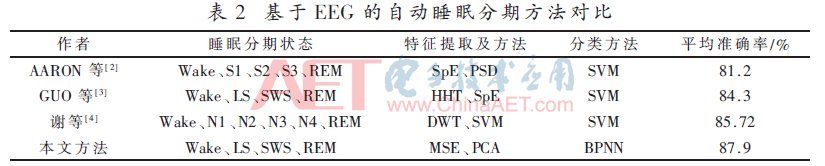
    本文主要对比了AARON等人^[2]、GUO等人^[3]、谢等人^[4]提出的自动睡眠分期方法，自动睡眠分期方法的对比如表2所示。发现本文所提方法对EEG信号睡眠阶段的分类准确性较高，同时PCA降低了系统的复杂性，模型的结构更为简单提升了系统的稳定性。

4 结论

    由于生理信号的特征提取和分类算法较为复杂，自动睡眠分期的准确率没有得到较大的提升。本文将MIT-BIH脑电EEG信号作为睡眠分期的生理数据样本，通过MSE-PCA模型将前2个主成分向量替代睡眠阶段的多尺度熵特征，不仅提取了EEG的非线性动力学特征，降低了模型的复杂性，而且更利于BPNN分类器对睡眠期的训练和分类。同时，自动分期的结果与数据库中的专家判定达到高度的一致性，说明MSE-PCA的融合方法能有效实现对EEG非线性特征的提取和降维，对睡眠过程的分析和研究有较大帮助。

参考文献

[1] 高群霞，周静，吴效明.基于脑电信号的自动睡眠分期研究进展[J].生物医学工程学杂志，2015，32(05)：1155-1159.

[2] AARON R S，LIANG C K.A study on sleep EEG using sample entropy and power spectrum analysis[C].Defense Science Research Conference and Expo(DSR)，Singapore，2011：1-4.

[3] GUO C，LU F，LIU S，et al.Sleep EEG staging based on Hilbert-Huang Transform and Sample Entropy[C].International Conference on Computational Intelligence and Communication Networks(CICN)，Jabalpur，2015：442-445.

[4] 谢宏，施小南.基于离散小波变换的脑电信号睡眠分期研究[J].微型机与应用，2015，34(432)：18-20.

[5] KEMP B.The sleep-edf database online.[Online].Available：http：//www.physionet.org/physiobank/database/sleep-edf/

[6] STOCHHOLM A，MIKKELSEN K，KIDMOSE P.Automatic sleep stage classification using EEG[C].Annual International Conference of the IEEE Engineering in Medicine and Biology Society(EMBC)，Orlando，2016：4751-4754.

[7] FRAIWAN L，LWEESY K.Newborn sleep stage identification using multi-scale entropy[C].IEEE 2nd Middle East Conference on Biomedical Engineering，Doha，2014：361-364.

[8] LIANG S F，KUO C E，HU Y H，et al.Automatic stage scoring of single-channel sleep EEG by using multi-scale entropy and autoregressive models[J].IEEE Transactions on Instrumentation and Measurement，2012，42(13)：1649-1657.

[9] 周鹏，李向新，张翼，等.基于主成分分析和支持向量机的睡眠分期研究[J].生物医学工程学杂志，2013，30(6)：1176-1179.

[10] 杨静，王成，谢成颖，等.基于主成分分析和反向传播神经网络的肝癌细胞后向散射显微光谱判别[J].生物医学工程学杂志，2017，34(2)：246-252.

[11] 王金甲，周丽娜.基于PCA和LDA数据降维的脑磁图脑机接口研究[J].生物医学工程学杂志，2011(6)：1069-1074.

作者信息：

刘雪峰1，马州生2，赵艳阳3，余传奇1，范文兵1

（1.郑州大学 信息工程学院，河南 郑州450001；2.河南省经贸学院，河南 郑州450046；

3.河南工业大学 电气工程学院，河南 郑州450001）