文献标识码: A
DOI:10.16157/j.issn.0258-7998.171650
中文引用格式: 侯玉涵,王耀力. 改进扩展卡尔曼滤波对四旋翼姿态解算的研究[J].电子技术应用,2017,43(10):83-85,93.
英文引用格式: Hou Yuhan,Wang Yaoli. Research on attitude solution of four-rotor based on improved EKF[J].Application of Electronic Technique,2017,43(10):83-85,93.
0 引言
四旋翼飞行器因为其结构简单对称、相对容易控制的特点,在监测、检查、救援、电子情报等很多重要的领域被广泛使用[1-2],最近几年在学术界和科研领域引起很大兴趣。四轴飞行器姿态角解算的速度和精度直接影响飞行器是否能获得实时、稳定的飞行姿态,所以姿态解算是四旋翼飞行器研究的核心之一。
对于四旋翼飞行器的姿态测量,采用集成了三轴陀螺仪和三轴加速度计的MPU6050进行姿态数据的采集,在较简单的硬件平台下,应该怎样滤除外部干扰,得到精确度比较高的数据变得十分重要。近几年姿态估计算法随着电子技术的发展相继出现。文献[3]应用互补滤波[3]对四旋翼的数据进行融合,该算法可以有效抑制因电机转动而带来的周期性干扰和因温度影响给MPU6050带来的漂移误差。但是应用互补滤波导致飞控系统有滞后现象,截止频率附近衰减较慢,处理后的数据存在误差,精确度较低。文献[4]提出基于欧拉角的迭代扩展卡尔曼[4](IEKF)姿态测量方法,该方法使用欧拉角方法描述姿态角,基于EKF滤波算法,在计算观测矩阵H时进行多次迭代,该算法估计出的姿态比普通EKF估计的姿态精度高。但该算法复杂、计算量大、循环周期长,仅适用于仿真,在实际工程上应用较少。文献[5-6]提出粒子滤波的算法,粒子滤波算法是在状态空间中寻找一组随机样本,近似地表示出概率密度函数,获得系统状态的最小方差,当样本数量趋于无穷时可以逼近任何形式的概率密度函数,摆脱了解决非线性滤波问题时随机量必须满足高斯分布的制约,因此粒子滤波能够比较精准地表达基于观测量和控制量的后验分布。但是粒子滤波需要大量的样本数量才能较准确地近似系统的后验概率密度,使得算法复杂度较高,而且重采样阶段会造成样本有效性和多样性的损失,导致样本出现贫化现象。
利用MPU6050采集姿态信息,为了获得较精确的姿态角,对EKF算法进行了改进,MPU6050在每一个采样时刻可以同时测得当前时刻飞行器的姿态角和姿态角变化率的信息,结合改进EKF算法对数据进行处理能够准确地估算飞行器当前的位置和姿态。飞行器在飞行过程中受非高斯白噪声的影响,本文在进行姿态解算时,为有效模拟飞行器测量过程的噪声,用两个加权高斯概率密度函数表示非高斯白噪声函数,选择合理高斯函数的权重、均值和方差。通过改进型EKF有效地滤除该噪声,减小了飞行器姿态偏差。
1 系统建模
为了获得四旋翼飞行器的姿态数据信息,首先选定两个基本坐标系:惯性坐标系E(XYZ)和机体坐标系B(X′Y′Z′)[7],如图1所示。


式中c代表cos,s代表sin,转换矩阵是非线性矩阵,为避免该矩阵出现奇点问题,飞行器在测试飞行过程中不会做出大幅度机动动作,因而可以认为系统满足以下假设:
(1)四旋翼飞行器横滚角与俯仰角满足以下不等式: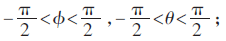
(2)在实际飞行中飞行器角速度信号由陀螺仪测量,因此可以假设飞行器横滚角速度与偏航角速度为有界信号L∞,即:wx∈L∞,wz∈L∞。
MPU6050可以快速、稳定地采集飞行器静止时的姿态信息,但当飞行器开始运动时,机体抖动及螺旋桨高频率的运动使得MPU6050测得的飞行器位姿存在明显的偏差。利用EKF将MPU6050采集的数据进行融合。EKF滤波原理是将非线性系统进行线性化处理,利用泰勒级数展开系统函数,取一次项作为EKF的系数矩阵,忽略了高阶项噪声。因此采用EKF进行姿态解算存在较大的滤波偏差。针对以上问题,本文提出改进型EKF,对四旋翼飞行器的姿态数据进行解算。
2 改进型扩展卡尔曼滤波原理及算法
为有效滤除噪声,测得精确的姿态数据,对EKF滤波算法进行了改进,采用两个EKF并行地对四旋翼飞行器的姿态数据进行预测和更新,将它们输出的状态变量加权整合后输出飞行器的最优状态估计,因此经改进EKF处理后的飞行器姿态数据达到最小均方误差。实现对飞行器位姿的有效操控,从理论上分析经过改进EKF滤波后的效果会更加接近真实值,有效地滤除噪声,且算法复杂度低、运算量小,不需要时频域的频繁转换,更不会因为样本数量的选择而导致样本重采样现象,融合后飞行器姿态数据精度高。具体步骤如下:
(1)EKF1 与EKF2 对四旋翼飞行器姿态数据并行地进行处理,输出对应的状态变量X1,k、X2,k和协方差P1,k、P2,k;
(2)计算EKF1 和EKF2的似然函数,求出对应的权重a1、a2;
(3)加权整合后更新四旋翼飞行器状态Xk和协方差Pk,输出飞行器姿态的最优估计;
(4)实时调整飞行器姿态,待飞行器下一个状态到达前返回步骤(1),继续下一次循环。
具体过程如图2所示。

对于一个随机系统,具体的估计过程如下:


3 仿真与实验
在改进型EKF理论的基础上进行仿真,在NI my RIO-1900的实验平台上对飞行器进行实验。
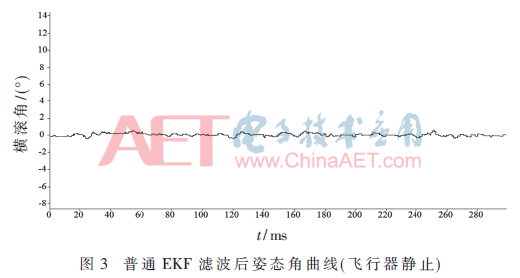
为保证飞行器初始时刻的稳定性及减小初始时刻姿态误差,对初始时刻四旋翼飞行器姿态数据进行滤波处理,以横滚角为例,采集飞行器静止时刻姿态数据,改进EKF滤波后姿态与普通EKF滤波后姿态进行对比,如图3、图4所示。普通EKF滤波后飞行器姿态有约1°左右的偏差,改进EKF滤波后飞行器姿态稳定性较好,偏差较小,几乎可以忽略。二者相比较,改进型EKF的滤波效果较好,鲁棒性强。

给飞行器横滚角一个操控命令,使其倾斜14°,飞行器在执行操控命令时,机体坐标系绕惯性坐标系旋转会产生一定旋转角,横滚角初始状态不是绝对的0°,经测试飞行器初始时刻横滚角为0.41°。如图5和图6所示,飞行器接收到操控命令后,普通EKF滤波后的飞行器经40 ms达到期望姿态,在140 ms 内有波动,140 ms 之后飞行器波动范围减小,但存在约0.5°左右的偏移。改进EKF滤波后的飞行器经38 ms后达到期望姿态,仅用时80 ms飞行器就达到理想状态,且偏移较小,可以忽略。从二者的对比图可得出,改进型EKF滤波后飞行器姿态角较稳定,提高了系统的准确性和可靠性。


通过MPU6050采集四旋翼飞行器0~100 s内的姿态数据,采集的姿态经改进EKF滤波后的动态测试如图7,在4 s~16 s、48 s~54 s、60 s~70 s、72 s~86 s、91 s~96 s时间段内,改进EKF估计值完全跟踪到理想值,在16 s~18 s、23 s~26 s、56 s~59 s、96 s~99 s时间段内,由于四旋翼飞行器姿态角度变化幅度较大,改进EKF估计值与理想值之间出现偏差,但在下一刻,即19 s、27 s、60 s、100 s时,改进EKF估计值快速恢复实时追踪。
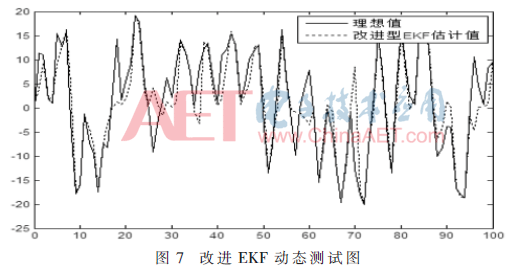
经计算,改进EKF估计值均方误差为3.306,普通EKF估计值均方误差为5.884 3。改进EKF估计值精度明显高于普通EKF估计值精度。精度提高的效率为:
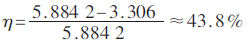
经过多次测试可知:该算法设计合理,姿态精度有较明显的改善,改进的算法已成功应用在四旋翼飞行器上,得到了理想的效果。
4 结论
本文改进的扩展卡尔曼了滤波算法,克服了非高斯白噪声对传感器姿态解算的影响,且该算法复杂度低、精度高、计算量小。实验结果表明,改进的算法可以准确地估计出姿态角,与经过普通EKF滤波后的姿态测量值对比,改进EKF在飞行器姿态精度上有较明显的改善,验证改进方法是有效的,为四旋翼无人机实时调整姿态提供了一种科学手段。该算法只对MPU6050采集的数据进行融合处理,进一步可将该算法应用至地磁计模块,对飞行器数据进一步进行融合处理,以快速实现飞行器的垂直起飞和悬停的控制操作。
参考文献
[1] ROSALES C,GANDOLFO D,SCAGLIA G,et al.Trajectory tracking of a mini four-rotor helicopter in dynamic environments-a linear algebra approach[J].Robotica,2015,33(8):1628-1652.
[2] LUPASHIN S,HEHN M,MUELLER M W,et al.A platform for aerial robotics research and demonstration:the flying machine arena[J].Mechatronics,2014,24(1):41-54.
[3] LU X,LI J,LIU W.A study of complementary filter algorithm for four-rotor helicopters attitude control system[J].Sensors & Transducers,2014,174(7):298-306.
[4] 贺海鹏,阎妍,马良,等.基于IEKF的四旋翼无人机姿态测量方法研究[J].计算机仿真,2015(4):56-60.
[5] MERCADO D A,CASTILLO P,LOZANO R.Quadrotors data fusion using a particle filter[C].Unmanned Aircraft Systems(ICUAS),2014 International Conference on.IEEE,2014.
[6] 曲仕茹,马志强.改进的粒子滤波在四旋翼姿态估计中的应用[J].飞行力学,2013(5):458-461,466.
[7] ZHAO S,AN H,LIU J,et al.Identification of aerodynamic parameter for quadrotor model[J].Journal of Electronic Measurement & Instrument,2013,27(8):744-749.
作者信息:
侯玉涵,王耀力
(太原理工大学 信息工程学院,山西 太原030024)

