文献标识码: A
DOI:10.16157/j.issn.0258-7998.170943
中文引用格式: 刘一兵,李荣宽. 一种基于传感器温度补偿的双指数函数拟合算法[J].电子技术应用,2017,43(11):47-50.
英文引用格式: Liu Yibing,Li Rongkuan. A double exponential function fitting algorithm based on sensor temperature compensation[J].Application of Electronic Technique,2017,43(11):47-50.
0 引言
目前基于传感器的温度补偿方法主要分为模拟硬件设计和数字信号处理两种方法。模拟硬件通常采用PTAT[1]和CTAT[2]等技术来设计读出电路。数字信号处理方法通常包括线性拟合、最小二乘多项式[4]拟合、BP神经网络[4]、卡尔曼滤波[3]、支持向量机等算法。本文在这些算法的基础上提出一种双指数函数模型的温度补偿算法,有以下优点:
(1)指数函数具有无限阶的泰勒展开式,因此双指数函数在对诸如传感器温度系数曲线这类非线性曲线的拟合上可以达到很高的精度。
(2)本文提出一种具有高精度初值的交替迭代法[5],即分离系数法。首先采用4组数据点,联立方程组,求出非线性系数的初始值,其次利用交替迭代法计算得到优化后的线性和非线性系数。整个算法解决了直接使用交替迭代法计算产生的迭代不收敛、精度较低、迭代次数较多的问题。
(3)在传感器温度补偿中,由于双指数函数系数只有4个,可以使用CORDIC算法设计硬件补偿电路来集成到传感器中,其中系数保存在ROM中即可,因此具有很好的工程实用价值。
1 交替迭代法拟合双指数函数
基于传感器温度补偿的双指数函数模型[6-7]为式(1)。


(5)重复步骤(2)、(3)和(4),使线性系数和非线性系数计算交替进行,直到均方误差Δ满足给定的范围为止。
交替迭代法仅使用非线性系数作为初值,在一定程度下降低了初值选取难度,不过对非线性系数依然有依赖性,因此在拟合过程中,非线性系数初值的选取就起到了至关重要的作用。
2 分离系数法计算非线性系数初值
本节采用分离系数法[9]来计算非线性初值。具体算法如下:
(1)在数据点中选择4组数据点{(Vtempi,Vouti)},i=1,2,3,4。其中Vtemp1<Vtemp2<Vtemp3<Vtemp4,且Vouti同号。
(2)将点1和点2带入双指数函数式(1)中得到式(4)和式(5):

(4)将点2和点3带入式(1)可以得到与式(6)类似的方程,二者联立可以消去线性参数α2,得到式(8),其中T2由式(7)下标加1得到。

(5)将式(8)两边取对数再近似带入中点微分消除对数可得式(9),其中中间变量A1、B1、C1、D1表达式由式(10)所示:

(6)再利用点2、3、4还可以导出类似于式(9)的方程,如式(11)。其中系数为式(10)下标加1即可。

(7)联立式(9)和式(11),消去一个非线性系数β2,求解一个一元二次方程组得到另一个非线性系数β1的两个解,再由式(9)求得β2。
分离系数法采用数据点对系数分离,最终将超越函数方程转换为一元二次方程求解。采用该方法时可以多次尝试不同的4点来对比拟合结果。一般来说,观测点相对密集和均匀时,误差相对较小。得到精度较高的非线性系数初始值后,将计算得到的初始值,利用第一节介绍的交替迭代法计算线性系数并优化结果,可以得到拟合精度较高的双指数函数方程,为温度补偿提供较为精准函数模型。
3 仿真实验与分析
3.1 双指数函数拟合
对两组数据(x1,y1)和(x2,y2)进行实验测试,具体数据见表1。
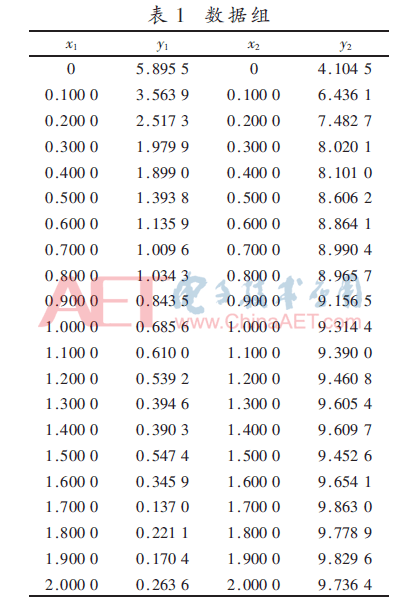
采用matlabR2013软件对数据(x1,y1)和(x2,y2)进行拟合。拟合结果如图1、图2所示。图1(a)和图2(a)采用本文提出的算法,首先算出高精度的非线性系数初始值,分别为β1=17.614 6、β2=1.314 7和β1=-0.092 9、β2=7.568 5,图1和图2(b)、图2(c)采用不同的线性初始值进行对比。表2和表3分别为对图1和图2三种拟合效果进行定量分析,使用均方根误差(RMSE)和确定系数(R_square)作为评价指标。


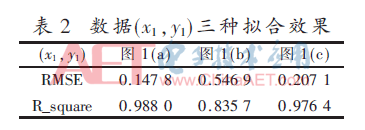

从表中结果可以看出,本文提出的算法,提高了初始值准确性,降低了均方误差,提高了确定系数,有较好的拟合效果。
3.2 基于传感器温度补偿
在本小节中,为了验证本文的算法和模型在传感器温度补偿中的有效性,使用一款MEMS加速度计,在温箱中进行零位温度循环实验。将采集到的数据进行预处理,具体步骤如下:
(1)实验数据导入MATLAB中进行数据理,取温度循环实验中的全温实验一段即Vtemp从0.4 V~0.67 V(实际温度相当于-40 ℃~60 ℃)。
(2)将数据进行小波降噪和剔除奇异值。
(3)采用移动平均法进行平滑处理并等间隔得采样50个数据点作为待拟合的数据。结果如图3(a)、图3(b)、图3(c)、图3(d)所示。
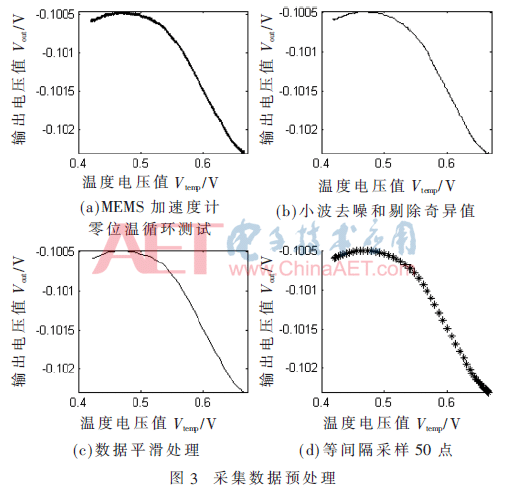
图4(a)、图4(b)为拟合结果图和最终补偿结果图。拟合结果RMSE=4.874 2×10-5,R_square=0.994 3。将MEMS加速度计原始输出进行补偿后,最大误差(峰峰值)从1.851 3×10-5下降到1.735 0×10-5。减少了一个数量级。

4 结束语
本文在现有温度补偿算法的基础上,首先提出了一种双指数函数模型的温度补偿方法。其次,在考虑到传统的交替迭代法进行双指数函数拟合过程中由于初值选取不当导致的迭代不收敛、精度较低、迭代次数较多的问题时,提出一种分离系数法 ,该方法能够有效地计算出高精度的初值,从而得到高精度的拟合结果。最终将算法应用到传感器温度补偿中,补偿结果表明温度系数曲线最大误差降低了一个数量级。具有一定实用价值。下一步可以采用CORDIC算法将双指数函数模型硬件实现,系数储存在ROM中,设计一款数字补偿电路集成到传感器芯片中,只需要改变4个系数,代替单片机,实现自动化的温度补偿。
参考文献
[1] ZHANG C,WU Q,YIN T,et al.A MEMS gyroscope readout circuit with temperature compensation,5th IEEE International Conference on Nano/Micro Engineered and Molecular Systems (NEMS),2010:458-462.
[2] YIN T,WU H,WU Q,et al.A TIA-based readout circuit with temperature compensation for MEMS capacitive gyroscope[C].IEEE International Conference on Nano/Micro Engineered and Molecular Systems(NEMS),2011:401-405.
[3] WU X,DUAN L,CHEN W.A Kalman filter approach based on random drift data of Fiber Optic Gyro[C].6th IEEE Conference on Industrial Electronics and Applications(ICIEA),2011:1933-1937.
[4] XIA D,CHEN S,WANG S,et al.Microgyroscope temperature effects and compensation-control methods[J].International Journal of Sensors 9,2009,10:8349-8376
[5] 陈华,邓少贵,范宜仁.同伦交替迭代法在双指数拟合中的应用[J].计算机工程与应用,2007,43(25):204-205.
[6] 韩丹,江春,付鹏涛,等.探测器信号波形离散序列的多项式与双指数曲线拟合及其在数字化核能谱中的应用[J].核电子学与探测技术,2010,30(8):1075-1078.
[7] 王永生,杜彬彬,孙瑾,等.Exponent及Gauss型遥测数据建模初始化算法[J].海军航空工程学院学报,2015,30(6):548-552.
[8] 赵林明,习华勇.数据拟合方法程序设计及其应用[M].石家庄:河北科学技术出版社,2000:79-80.
[9] 朱珉仁.确定双指数曲线参数初始值的循环搜索法[J].数学的实践与认知,2003,33(12):73-77.
作者信息:
刘一兵,李荣宽
(电子科技大学 电子工程学院,四川 成都611730)

