0 引言

    传统的信息隐藏算法在嵌入隐秘信息的同时会对载体图像造成永久性的损坏，而这些损坏在一些对数据认证要求较高，同时需要对原始载体进行无失真恢复的应用场合是不可接受的。比如医学影像的处理、法律取证、军事图像传输等。可逆信息隐藏作为信息隐藏技术的重要分支，能同时满足信息嵌入和无失真的恢复载体的要求^[1]。密文域可逆信息隐藏是指用于嵌入的载体是经过加密的，嵌入信息后仍然可以无差错解密出载体的技术^[2]。可逆信息隐藏方法主要包括：基于无损压缩^[3-4]、差值扩展^[5-7]和直方图平移^[8-10]。预测误差扩展^[11]属于差值扩展的一类，关键在于提高预测算法的准确度，以达到提高嵌入容量的目的。文献[11]提出根据图像区域的纹理复杂度选择性地嵌入秘密信息，但是只是选择图像平滑区域进行预测，对于纹理复杂区不变，嵌入容量有限。文献[12]对于图像均匀区域，利用水平像素平均值与垂直像素平均值之差表示预测像素值，对于图像非均匀区域，利用水平或垂直像素对的平均值作为像素的预测值。文献[13-15]利用局部边缘信息的修改提高预测精度，但是嵌入量提高有限，而且运算复杂度较高。文献[16]提出利用预测误差对进行可逆信息隐藏，对于像素的修改值最大为2，嵌入容量并不是很高。现有的预测误差算法多是针对明文域，具有嵌入容量高、计算复杂度低等特点，但是在密文域的应用有限。本文采用插值预测误差的方法，在保证预测算法的精度的前提下，提高信息嵌入容量。同时对于图像的像素点采用两种方式进行加密操作，在信息提取的过程中既能够在加密域操作，也能够在解密域操作，使得算法的可分离性和可逆性得到保证。

1 相关知识

    Paillier加密方案^[17]是一种具有加法同态性质的同态方案，其加密和解密机制如下：随机选择两个大素数p和q，满足gcd(pq，(p-1)(q-1))=1，计算n=pq，λ=lcm(p-1，q-1)。其中，lcm指最小公倍数，公钥为(n，g)，私钥为λ。

    由式(4)、式(5)可以看出密文域的乘法对应明文域的加法，而明文域的乘法对应密文域的幂的运算。

2 基于插值预测误差扩展的可逆信息隐藏

2.1 预处理过程

    假设原始图像是一副灰度图像，大小为N×N，像素值p(i，j)∈[0，255]，1≤i≤N，1≤j≤N。同时将图像的像素分为三类：第一类像素点是原始图像的像素点，即采样像素点(Sample Pixels，SP)，如图1中显示的深色的点，用p_SP表示，取值范围为：p_SP=p(2·i-1，2·j-1)，i，j=1，2，3，…，N/2；第二类像素点是需要插值的像素点，即非采样像素点(Non-Sample Pixels，NSP)，再将这些点分为三类，分别对应图1(b)(c)(d)中的①②③，分别记为pNSP1、pNSP2、pNSP3；第三类像素点是用于嵌入边信息，如图1(b)中所示的白色像素点。

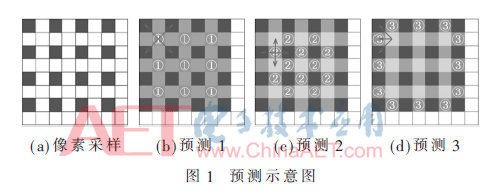
    对像素点分好类之后，先对①号像素点进行预测，①号像素点坐标可表示为p_NSP1=p(2·i，2·j)，i，j=1，2，3，…，N/2，主要利用距离其最近的4个原始像素点进行预测，其坐标分别是：p₁=p(2·i-1，2·j-1)，p₂=p(2·i-1，2·j+1)，p₃=p(2·i+1，2·j-1)，p₄=p(2·i+1，2·j+1)。

    方法步骤如下：

    在同一列上的像素点插值是利用同一列上的原始像素点和已经预测的①号像素点算法是：

其中，hist(e)表示在直方图上误差值为e的对应像素的个数，E表示预测误差的集合，通常情况下RP≥0，LP<0。

    将预测误差集合分为两部分：

    (1)左侧插值预测误差LE：满足e′(i，j)<LP；

    (2)右侧插值预测误差RE：满足e′(i，j)>RP。

    用LN和RN分别表示直方图中的两个最低点对应的预测误差值，表达式为：

    通过实验证明，本文插值算法计算出的像素点与原始像素点很接近，因此插值误差多为0。同时本算法的加密过程利用模运算能有效地避免溢出的发生。

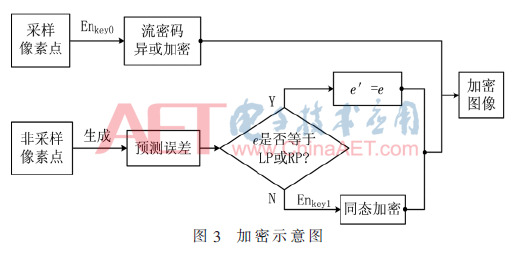
2.2 图像加密过程

    加密过程如图3。对于图像采用两种方式进行加密。对于采样像素点使用序列密码加密。将像素点表示为8位，如式(16)所示；按位将其与伪随机比特位相异或，如式(17)所示：

    此时得到一幅加密后的图像，图像的像素值可以表示为：

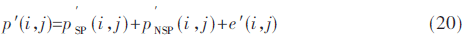
2.3 信息嵌入过程

2.4 信息提取过程

    在本方案中，隐藏的秘密信息既可以在加密域提取，也可以在解密域提取。信息提取与图像恢复如图4。

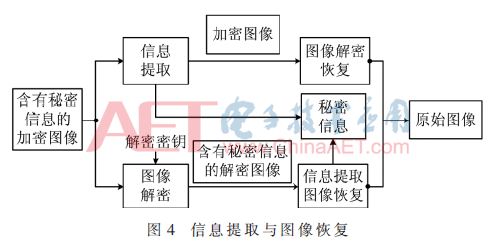
2.4.1 加密域信息提取与图像恢复

    根据信息的嵌入密钥从图像的边缘区域的最低有效位中获得LP、LN、RP、RN数值，根据信息可以提取出秘密信息并计算出加密之后的预测误差值，如式(24)、式(25)所示：

    当接收方同时拥有解密密钥时，就可以解密图像，进而得到原始载体图像。具体解密步骤如下：

    整个提取信息的过程都是在加密域中进行的，这样可以有效地避免原始图像的内容泄露。同时，嵌入的秘密信息能够被无失真地恢复。

2.4.2 解密域信息提取与图像恢复

    (2)信息提取与图像恢复

    ①提取隐藏的秘密信息并恢复原始预测误差值，如式(26)、式(27)所示：

    本节信息提取是在明文域进行，从文中算法可以看出，先解密图像并不会对秘密信息造成破坏，秘密信息和原始载体图像能够无失真地恢复。

3 仿真实验与算法分析

    利用MATLAB R2008b仿真实现了本文提出的可逆信息隐藏算法，使用512×512的灰度图像，图5分别为常见图像Lena、Baboon、Airplane和Hill的原始图像。

    通过对原始图像进行采样并预测，生成预测图像，进一步得到预测误差图像，生成预测误差图像的直方图，如图6所示。以图6(a)为例，该图为Lena图的预测误差图像生成的直方图，从图中可以看出，峰值点为数值为0的点，即为该文中用于嵌入秘密信息的点，以及1和-1的点也可以用于秘密信息的嵌入，这样既能够保证数据的嵌入容量，又能够保证嵌入之后的图像质量。

    生成预测误差图像之后，利用序列密码加密采样像素点，用Paillier同态算法加密非采样像素点，之后根据图6中选出的峰值点进行直方图平移的操作达到嵌入秘密信息的目的。图7即为加密后且嵌入秘密信息之后的图像，分析图7可以看出，由于图7(a)和图7(c)的原始图像纹理较为平滑，因此预测的相对较为准确，所以加过密之后的载体图像的基本纹理仍然能够看得出来；而对于图7(b)和图7(d)的图像纹理较为复杂，相比预测有一定误差，所以加密之后的图像基本的纹理不易看出来。

    当接收方收到含有秘密信息的加密图像后，根据掌握的密钥情况，若只有解密密钥，则只能对图像进行解密操作；若只有嵌入密钥，则只能在加密图像之中提取秘密信息而无法获得原始图像的内容；若同时掌握解密密钥和嵌入密钥，则可以获得原始图像和秘密信息，并且信息提取与图像恢复没有先后之分，可以根据接收方的需要进行操作。图8为解密后含有秘密信息的图像，通过实验验证图像的PSNR值均高于45 dB，通过人眼难以辨别出图像由于嵌入信息而引起的失真。

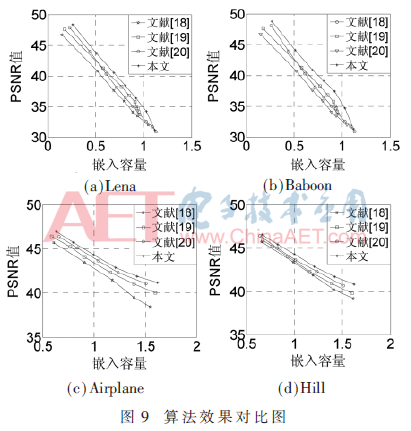
    将本文算法与之前算法进行对比，如图9和表1、表2所示，包括最大嵌入容量和PSNR的统计。分析图9可以看出，本文的算法性能好于之前的算法。表1表示在图像均嵌入50 000 bit秘密信息时，统计得到的不同图像的PSNR值，分析得出当嵌入量相同时，本文算法得到的图像的PSNR值更高，效果更好。分析表2可以看出，当PSNR值相同且均为45 dB时，本文算法的嵌入容量高于现有算法。

4 结论

    本文提出了一种改进的预测误差算法并将其应用于密文域，该方案使用插值技术生成被称为插值预测误差的剩余价值。通过对这些插值预测误差进行加法扩展，实现了一个高效的密文域可逆信息隐藏算法。根据实验结果，本文提出的可逆隐写算法能够提供更高的嵌入容量，获得更好的图像质量，同时能够保证一定的安全性。但是算法的安全性还没有达到最好，下一步将利用更加合适的加密算法进行加密，同时如何根据原始载体图像的纹理特征自适应地进行预测，提高预测精度和嵌入容量也是下一步的研究重点。

参考文献

[1] ZHANG X.Reversible data hiding in encrypted image[J].IEEE Signal Processing Letters，2011，18(4)：255-258.

[2] 张敏情，柯彦，苏婷婷.基于LWE的密文域可逆信息隐藏[J].电子与信息学报，2015，38(2)：354-360.

[3] JARALI A，RAO J.Unique LSB compression data hiding method[J].International Journal of Emerging Science and Engineering，2013，2(3)：17-21.

[4] KHAN A，SIDDIQA A，MUNIB S，et al.A recent survey of reversible watermarking techniques[J].Information Sciences，2014，279：251-272.

[5] TIAN J.Reversible data embedding using a difference expansion[J].IEEE Trans.Circuits Syst.Video Techn.，2003，13(8)：890-896.

[6] THODI D M，RODRIGUEZ J J.Expansion embedding techniques for reversible watermarking[J].IEEE Transactions on Image Processing，2007，16(3)：721-730.

[7] TSENG H W，CHANG C C.An extended difference expansion algorithm for reversible watermarking[J].Image and Vision Computing，2008，26(8)：1148-1153.

[8] LI X，LI B，YANG B，et al.General framework to histogram-shifting-based reversible data hiding[J].IEEE Transactions on Image Processing，2013，22(6)：2181-2191.

[9] DONG L，ZHOU J，TANG Y Y，et al.Estimation of capacity parameters for dynamic histogram shifting(DHS)-based reversible image watermarking[C].2014 IEEE International Conference on Multimedia and Expo(ICME).IEEE，2014：1-6.

[10] HU X，ZHANG W，LI X，et al.Minimum rate prediction and optimized histograms modification for reversible data hiding[J].IEEE Transactions on Information Forensics and Security，2015，10(3)：653-664.

[11] LI X，YANG B，ZENG T.Efficient reversible watermarking based on adaptive prediction-error expansion and pixel selection[J].IEEE Transactions on Image Processing，2011，20(12)：3524-3533.

[12] DRAGOI C，COLTUC D.Improved rhombus interpolation for reversible watermarking by difference expansion[C].Signal Processing Conference(EUSIPCO)，2012 Proceedings of the 20th European.IEEE，2012：1688-1692.

[13] FENG G，FAN L.Reversible data hiding of high payload using local edge sensing prediction[J].Journal of Systems and Software，2012，85(2)：392-399.

[14] YANG W J，CHUNG K L，LIAO H Y M，et al.Efficient reversible data hiding algorithm based on gradient-based edge direction prediction[J].Journal of Systems & Software，2013，86(2)：567–580.

[15] LU T C，TSENG C Y，DENG K M.Reversible data hiding using local edge sensing prediction methods and adaptive thresholds[J].Signal Processing，2014，104：152-166.

[16] OU B，LI X，ZHAO Y，et al.Pairwise prediction-error expansion for efficient reversible data hiding[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society，2013，22(12)：5010-21.

[17] PAILLIER P.Public-key cryptosystems based on composite degree residuosity classes[C].Lecture Notes in Computer Science，1999，5：223-238.

[18] CHANG Y T，HUANG C T，LEE C F，et al.Image interpolating based data hiding in conjunction with pixelshifting of histogram[J].The Journal of Supercomputing，2013，66(2)：1093-1110.

[19] LU T C，CHANG C C，HUANG Y H.High capacity reversible hiding scheme based on interpolation，difference expansion，and histogram shifting[J].Multimedia Tools and Applications，2014，72(1)：417-435.

[20] XU D，WANG R.Reversible data hiding in encrypted images using interpolation and histogram shifting[M].Digital-Forensics and Watermarking，2015.

作者信息：

牛向洲，张敏情，柯  彦

(武警工程大学 电子技术系 网络与信息安全武警部队重点实验室，陕西 西安710086)