0 引言

    粒子群优化(Particle Swarm Optimization，PSO)算法^[1]是由KENNEDY J和EBERHART R C等开发的一种新的进化算法。相对于遗传算法^[2]等，该算法参数较少、容易实现，能够解决复杂的优化问题，因此在众多优化问题领域都得到了广泛的应用^[3]，如控制决策、目标跟踪、深度学习等。然而，粒子群优化算法在实际应用中往往难以达到实时性的要求，特别是求解复杂的多维问题时，速度问题更加突出，难以满足实际应用的需求。

    随着嵌入式领域对性能、功耗和成本越来越高的要求，多核处理器应运而生^[4]。其中TI公司推出的基于KeyStone架构的多核处理器TMS320C6678^[5]是目前业界最高性能的量产多核DSP。其具有8个1.25 GHz DSP内核，最高可实现160 GFLOP的性能。与FPGA相比其具有更好的浮点性能和实时处理能力，并且具有较高的灵活性和可编程性，为实现更为复杂的算法提供了便利。因此其在4G通信、航空电子、机器视觉等领域得到了广泛的应用。

    本文针对粒子群算法在实际应用中的实时性需求，在对算法进行并行性分析的基础上，根据TMS320C6678多核处理器的架构特点，设计出高效的应用程序，充分发挥了TMS320C6678的性能优势，有效地提高了系统的实时处理能力。实验数据表明了该设计的合理性与有效性。

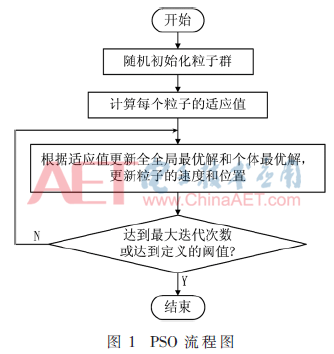
1 PSO算法简介

    PSO流程图如图1所示。粒子群算法的数学描述如下：m维的解空间中，X={x₁，x₂，…，x_n}表示整个种群，该种群由n个粒子组成。因此整个种群中的第i个粒子的位置可以表示为x_i={x_i1，x_i2，…，x_im}，该粒子对应的求解速度可以表示为v_i={v_i1，v_i2，…，v_im}，每个粒子对应的个体最优解表示为p_i={p_i1，p_i2，…，p_im}，整个种群的全局最优解可以表示为g_i={g_i1，g_i2，…，g_im}。在每一次的迭代中，每个粒子将个体最优解pbest和全局最优解gbest作为飞行经验，根据如下公式来更新自己的速度和位置：

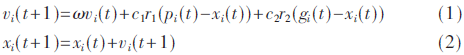
式中，t表示当前迭代次数，x_i(t)对应粒子当前时刻的位置，x_i(t+1)对应粒子下一时刻的位置，v_i(t)和v_i(t+1)分别表示粒子当前时刻和下一时刻的速度，ω为惯性因子，c₁和c₂为学习因子，r₁和r₂表示在0~1之间的随机数。此外在每一维，粒子都有最大的限制速度v_max，如果v_i>v_max，则有v_i=v_max；如果v_i<v_max，则有v_i=-v_max。

2 多核DSP任务并行设计

2.1 算法并行性分析

    粒子群算法和其他一些进化算法相比，其优势在于步骤简单、参数少、容易实现、无需梯度信息等。更重要的是粒子群算法是一种并行算法，非常适合在多核处理器上实现其并行计算。算法中各个粒子具有很高的独立性，所以各个粒子可以独立地完成信息的更新，从根本上实现各个粒子间的并行操作处理，提高算法的实时性。根据处理器的核心数，将粒子的更新任务平均映射到8个核上。运行时使用如下基本测试函数对该方案进行验证：

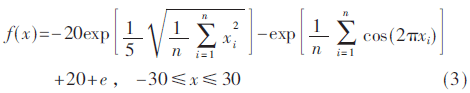
其中，n表示维数，该函数在x=(0，0，…，0)处取得全局最小值f_max=0。另外该函数比较复杂，是一个多峰函数。

2.2 并行处理模型设计

    将程序映射到多核处理器的第一步就是确定任务的并行性，并选择一种最合适的处理模型。前面已经分析了算法的并行性。

    两种最主要的模型是主从模型和数据流模型^[6]，分别如图2、图3所示。主从模型是一种控制集中、执行分布的模型。数据流模型代表分布式控制和执行。除此之外还有OpenMP模型^[7]，该模型是一种在共享内存并行体系中应用发展多线程的应用程序编程接口，如图4所示。

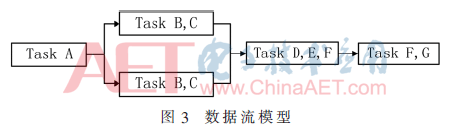
    结合前面算法的并行性分析，考虑到处理流程时间上的并行性和空间上的并行性，这其中包含了流水操作和并发操作，使用单一的模型都无法有效地解决，因此，突破性地将二者结合起来，设计出局部并行全局串行的并行模型，如图5所示，从而取得良好的并行度和加速比，这在测试数据及结果分析中可以看出。

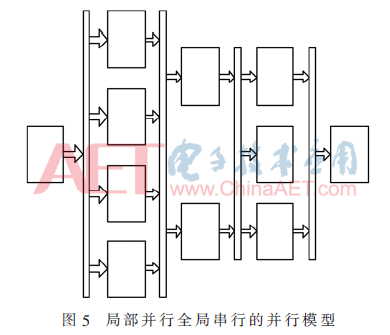
2.3 处理器之间的通信交流

    多核处理器中内核之间如何进行高效的通信交流，是多核系统所面临的主要难点。处理器之间的通信交流主要包括数据移动和同步^[8]。TMS320C6678提供了多种处理器之间的通信机制。软件是基于SYS/BIOS实时操作系统开发的。考虑到开发的难易程度及性能，采用IPC核间通信的组件来完成核间数据搬移和同步。该组件有“消息队列”(MessageQ)和“通知”(Notify)两种模型。除了Notify通知机制，还可以利用MessageQ来实现更为复杂的核间通信。考虑到需要同时实现数据搬移和同步，所以采用“消息队列”(MessageQ)模型。0核作为主核负责向从核发送事件，激活从核并进行一定的运算。主核与从核之间有相互连接。1~7核为从核，主要负责运算，从核之间没有连接。

3 基于TMS320C6678的PSO算法的实现

    软件部分是基于SYS/BIOS操作系统开发的，同时利用IPC组件。在实现过程中，利用DSP集成开发环境CCS5.2进行相应的编程开发。SYS/BIOS用来实现核间任务调度，IPC用来实现核间同步和通信。

    基于TMS320C6678的PSO算法系统框图如图6所示。首先是系统启动，8个核进行相应的初始化配置。初始化配置之后调用Ipc_start()函数将自动实现相应模块的配置，各个核进入同步等待的状态，直到8个核都进入同步等待状态，程序才会继续执行。一般情况下，在使用IPC组件时直接让每个核同所有核之间都有连接，而且各核之间连接都是相同且双向的，这样的配置方法并不高效，影响运行效率。因此这里有选择地进行核间连接，使用Ipc.ProcSync_PAIR在.cfg文件中进行配置，之后使用Ipc_attach()函数仅仅在主核与从核之间建立双向连接。主核首先进行整个粒子群的初始化，主要包括随机产生粒子的位置和速度，计算出每个粒子的适应度值作为局部最优解，求出对应的全局最优解等任务。主核在完成初始化工作后，将数据分为8份，通过MesssageQ_put()函数将每个核对应的数据的地址发送到对应的核，并启动从核进行相应的处理。之后所有的核进行循环迭代处理，实现算法对应的进化寻优处理。同时判断当前解是否满足预定的最小适应阈值或达到最大迭代次数。最后直到从核完成迭代，通知主核完成所有运算，输出最优解。

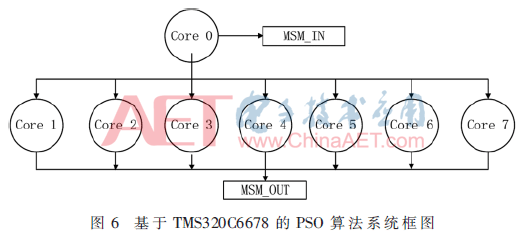
4 实验结果分析

4.1 存储空间分析

    KeyStone架构是一款精心设计且效率极高的多核心内存架构，其具备3个存储等级^[9]。处理器的每个内核都拥有自己的一级程序（L1P）和数据(L1D)存储器，均为32 KB大小，这里默认配置成cache使用。二级存储器L2可以做代码和数据存储器，为了提高程序性能，这里把L2的32 KB大小的空间也设置成cache，其余空间用作SRAM。当数据量太大时需要将数据置于DDR3中。该实验中设计粒子的个数为50，维度也为50，则算法对应的数据量大概为60 KB。另外考虑到共享存储器有4 MB大小，可以将程序运行涉及的主要数据存放在共享存储器里，包括粒子的位置、速度、个体最优解、全局最优解等。占用全部片内共享存储器（MSM）资源的1.5%左右。CCS仿真时的平均收敛曲线如图7所示。

4.2 运行时间分析

    TMS320C6678处理器每个内核频率为1.25 GHz，可以提供每秒高达40 GB MAC定点运算和20 GFLOP浮点运算能力；1片8核的TMS320C6678提供等效达10 GHz的内核频率，单精度浮点并行运算能力理论上可达160 GB FLOP。实验中有关算法的运行时间是通过C语言库中的clock()函数测量的。处理器运行时的主频配置为1.0 GHz，则算法迭代500次时运行时钟数如表1所示。

    由表1可以看出，基于TMS320C6678的PSO算法系统得到了较好的核间通信和并行处理性能。在相同的参数环境下，该系统的处理能力是C66x单核的5.19倍。实验结果表明，基于TMS320C6678的并行粒子群算法的实时处理能力有显著提升。

4.3 加速比和并行效率

    加速比^[10]和并行效率是衡量并行处理器性能的两个重要的指标。加速比(Speedup Rate)用来衡量并行系统或程序并行化的性能和效果。并行效率(Parallel Efficiency)表示在并行机执行并行算法时，平均每个处理机的执行效率。下面根据Amdahl定律^[11]来具体计算加速比和并行效率。

    假设一个任务在有N个单元的处理器上运行，其中可并行执行的部分为T_p，只能串行的部分为T_s。则在单处理器上运行时间为T_ser=T_s+T_p，T_par=T_s+T_p/P。这里用Sr来表示加速比，则根据表1测试的数据可以求出该系统的加速比如下：

    通过以上分析可以看出，通过增加并行处理单元个数可以提高加速比，但是其增加的倍数和增加的处理器的个数并不是严格对应的。这是因为处理器个数的增加会带来额外的通信开销，甚至在某些情况下会导致系统效率的下降。因此在设计系统时，应综合考虑处理单元个数、并行结构设计和任务的映射等因素。

5 结论

    本文针对粒子群算法在实际应用中的实时性需求，首先对算法进行并行性分析，并根据TMS320C6678多核处理器的架构特点，设计出局部并行全局串行的并行模型，高效地将应用程序映射到多核处理器。该设计也适用于其他架构的并行处理器，具有广泛的应用性。实验数据表明该设计充分发挥了TMS320C6678的性能优势，与单核处理相比有效提高了系统的实时处理能力。因此，该设计有效地推进了PSO算法在实际中的应用，对其他各种群智能算法有重要的借鉴意义。

参考文献

[1] KENNEDY J，EBERHART R C.Particle swarm optimization[C].IEEE International Conference on Neural Networks，1995：1942-1948.

[2] DEB K，PRATAP A，AGARWAL S，et al.A fast and elitist multiobjective genetic algorithm：NSGA-II[J].IEEE Transactions on Evolutionary Computation，2002，6(2)：182-197.

[3] Jin Nanbo,RAHMAT-SAMII Y.Advances in particle swarm optimization for antenna designs：real-number，Binary，single-objective and multiobjective implementations[J].IEEE Transactions on Antennas and Propagation，2007，55(3)：556-567.

[4] 郝朋朋，周煦林，唐艺菁，等.基于TMS320C6678多核处理器体系结构的研究[J].微电子学与计算机，2012，29(12)：171-175.

[5] Texas Instruments.TMS320C6678 mulicore fixed and floating-point digital signal processor[Z].2010.

[6] Texas Instruments. Multicore programming guide(Literature Number：SPRAB27B)[Z].2011.

[7] 牛金海.TMS320C66x KeyStone架构多核DSP入门与实例精解[M].上海：上海交通大学出版社，2014.

[8] 吴灏，肖吉阳，范红旗，等.TMS320C6678多核DSP的核间通信方法[J].电子技术应用，2012，38(9)：11-13.

[9] Texas Instruments.KeyStone architecture multicore shared memory controller(MSMC)(Literature Number：SPRUGW7A)[Z].2011.

[10] 谢超，麦联叨，都志辉，等.关于并行计算系统中加速比的研究与分析[J].计算机工程与应用，2003，39(26)：66-68.

[11] 李文石，姚宗宝.基于阿姆达尔定律和兰特法则计算多核架构的加速比[J].电子学报，2012，40(2)：230-234.