文献标识码: A
DOI:10.16157/j.issn.0258-7998.171767
中文引用格式: 余成波,李彩虹,曾亮. K-means指纹定位的优化算法[J].电子技术应用,2018,44(2):70-74.
英文引用格式: Yu Chengbo,Li Caihong,Zeng Liang. Optimization algorithm of K-means fingerprint location[J]. Application of Electronic Technique,2018,44(2):70-74.
0 引言
在智能终端快速更换的时代,人们生活水平不断提升,图书馆、博物馆等室内场景需提供精确位置信息来提供服务。技术成熟的全球定位系统(Global Positioning System,GPS)已实现了应用范围广、精度高、实时性好的室外定位[1],但在室内中受复杂环境因素的影响,GPS信号因受阻挡而急速衰减,无法满足人们的室内定位需求,因而催生出很多室内定位技术。其中,配备有蓝牙技术的iBeacon因其功耗低、成本低、效率高等优点备受人们的青睐。
iBeacon主要通过基于接收信号强度指示(Received Signal Strength Indication,RSSI)的位置指纹实现定位,即通过智能终端测量RSSI,依据采样点间RSSI的差异构建位置指纹库[2],再利用匹配定位算法得到定位结果。但是当定位区域较大时,指纹库中存储的位置信息较多,导致运算量过大并影响定位精度。对此,文献[3-6]采用K-means算法对指纹库进行聚类分析,选出相似度最高的子库进行匹配定位。该方法不仅可降低计算的负荷与能耗,还可有效提高定位的实时性。然而其多是依据经验选定聚类的个数,未对聚类优劣进行说明;且通过待测点与聚类中心的欧式聚类判断其所属类别,并未考虑各个变量之间的相关性。
针对上述存在的问题,本文提出优化算法:采用两步聚类算法根据AIC准则自动选定最优聚类情况,利用相关系数法得到与待测点最相似的子库,最后采用K邻近法与子库匹配得到定位结果。
1 K-means指纹定位
K-means指纹定位是在原指纹定位算法的基础上,先对指纹库进行聚类分析,再通过匹配算法估计待测点位置的一种算法。即离线阶段,构建指纹库后,通过K-means聚类根据特征参数将指纹库划分为k个子库;匹配阶段,首先比较待测点与各聚类中心的相似程度,选取距离最短的聚类中心所在的子库,再将其与待测点匹配估计最终坐标。具体操作流程如图1所示。

1.1 K-means聚类
指纹库中第i个参考点(Reference Point,RP)接收到接入点(Access Point,AP)的RSSI信号记为RSSIi=[RSSIi1,…,RSSIij,…,RSSIin],j=1,…,n,其中RP的个数为m,AP的个数为n。由其构建指纹库的RSSI=[RSSI1,RSSI2,…,RSSIi,…,RSSIm]T,i=1,…,m。已知聚类数目为k(k≤m)的前提下,将指纹库的RSSI分为k类RSSI=[C1,C2,…,Ck],随机选用k个向量作为初始聚类中心,以欧氏距离作为相似度准则就近分配指纹数据,不断迭代更新聚类中心,直至算法收敛或达到最大迭代次数。当总的类间离散度最小时认为算法收敛,即:

式中,k为聚类个数,Centert为第t个聚类中心。具体算法流程[7]如下。
K-means算法流程:
输入:从指纹库的RSSI中随机选取k个向量作为初始聚类中心;
输出:最终聚类结果。
For i=1:k
(1)计算样本中各指纹到每个聚类中心的距离,并根据就近原则分配指纹到不同类中;
(2)分配完样本中指纹后,重新计算k个聚类的中心;
(3)计算总的类间离散度Jc
If Jc最小,即算法收敛
Break;//跳出循环,结束迭代过程
End
End
1.2 匹配算法
本节所介绍的算法,主要选取相似度最高的子指纹库,并估计待测点的最终位置。
1.2.1 最邻近法
最邻近法(Nearest Neighborhood,NN)是最简单、最基础的算法,首先算出待测点RSSI与指纹库中各指纹的RSSI之间的距离,再选取距离最短的指纹坐标值作为待测点的估计位置。其中距离的公式为:

式中,Di表示待测点与第i个RP的距离,Sj表示待测点接收到第j个AP的信号强度,RSSIij表示第i个RP接收到第j个AP的信号强度。q=1时是绝对距离,q=2时是欧式距离,通过实际情况分析后选取合适的距离公式。
1.2.2 K邻近法
K邻近法(K Nearest Neighborhood,KNN)是对最邻近法的改进,其区别主要在于K邻近法并不直接选择距离最短的一个指纹来估算位置,而是选择距离最短的前K(K≥2)个指纹,并将这K个指纹的平均坐标作为最后的估计位置。即通过式(2)得到距离后将位置从小到大排序,选取前K个指纹坐标,利用式(3)计算出均值坐标并输出最后结果。

式中,(xi,yi)表示排序后选取的前K个指纹中第i个指纹的坐标值。
1.2.3 相关系数法
相关系数法通过计算两个物体间的相似程度[8],判断其距离的相对大小。地理学第一定律[9]指出,任何两个物体之间都是相似的,只是相似程度的大小不同,并且其相似程度随着距离的增加在不断减少。
在定位范围内,假设A、B两个待测点空间位置很近,其接收到AP的RSSI分别记为RSSIA=[SA1,SA2,…,SAn]和RSSIB=[SB1,SB2,…,SBn],根据式(4)计算两点间的相关系数:

式中,ρ(A,B)为两点间相关系数,(xi,yi)为所取K个指纹中第i个的坐标值。
由前面分析可知,K-means聚类需要预先给定聚类的数目,其多是依据经验进行选择并通过定位精度评估聚类的质量。而在实际情况中影响定位精度的原因有很多,所以需要一种准则来评估聚类结果。两步聚类是一种探索性聚类方法,通过分析数据间类别结构来构建聚类模型,根据AIC准则评估聚类质量并择优选出聚类个数。
2 优化后的指纹定位
2.1 AIC准则
AIC准则[11]是日本统计学家赤池宏次提出关于衡量统计模型优良的一种标准,主要在模型复杂度和参数个数之间找到一种平衡,从而选择最优模型。其定义为:

其中,k为参数的个数,L为样本集上的极大似然函数。为优化其拟合性可增加参数的个数,但要注意防止出现过度拟合。给定一组参数模型时,要优先考虑AIC值最小的模型,因为它包含最少的参数个数又最大程度地还原数据模型。
文献[12]给出了利用AIC准则选取最邻近聚类模型的具体理论分析,分析发现:类内误差随聚类数目k的增加而越小,为考虑聚类模型的紧凑型与实用性,选择AIC值最小的聚类模型,即可得到最优的分类情况。
2.2 两步聚类
两步聚类是一种探索性聚类方法,主要有两个阶段,其具体流程如图2所示。

(1)预聚类阶段:构建聚类特征树(Clustering Feature Tree,CFT),将指纹库分为许多子库。
首先,将某一个观测值置于根节点处并记录相关变量信息,根据给定的距离公式作为相似性依据,依次判断其他测量值与已有节点的相似性并进行分类,若没有相似节点,则生成新节点。所有RP分类后,根据AIC准则,确定预聚类的数目。
(2)正式聚类阶段:合并聚类,给出最终优化的聚类数目。
将预聚类的数目作为数据输入,使用分层聚类对其进行再聚类不断合并修剪预聚类结果,通过AIC准则评估现有分类的质量,最终给出符合准则的分类方案。
2.3 优化算法
K-means随机选取聚类个数与聚类中心带来极大的不稳定性,对此使用两步聚类算法选择最优聚类数并对其分类。文献[10]分析实验数据发现:RSSI相关系数匹配法比NN匹配定位精度高,但是实时性差。为提高定位精度、增强算法实时性,本文使用相关系数法选取子指纹库,使用KNN算法估计待测点位置。具体操作如图3所示。

3 实验布置与结果分析
3.1 实验环境
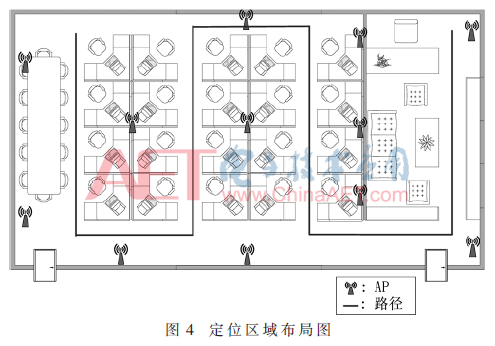
本实验在8 m×14 m的典型办公环境中进行,室内布局情况如图4所示,将信标节点AP呈大致均匀摆放,此区域放置12个AP。经测试发现,采集的RSSI数据在1 m范围内波动较小,由此可将定位区域划分为1 m×1 m的小区域,并在每个区域顶点采集数据,为消除方向引起的误差,在每个RP不同方向进行采样。受物体摆放情况的影响,最终共采集438组数据。根据移动路径(图4中路径),采集107组数据。
3.2 实验分析
为方便讨论定位效果,需选定合适的参数指标对其进行说明。一定程度上,平均定位误差可反映算法的整体效果,定位误差的标准差可说明定位精度的一致性[13];运算时间可反映算法的实时性。本文主要从考虑算法的精度和实时性出发,因而选用平均定位误差、误差的标准差和运算时间来判断算法的定位效果。
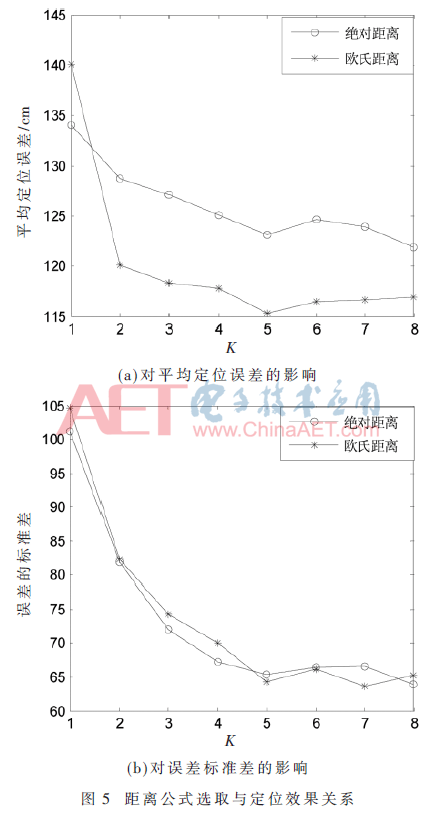
本文重点讨论聚类算法对定位结果的影响,为排除其他因素的影响,首先利用传统指纹定位选择最优的距离公式与K值,实验结果如图5所示。观察图5(a)可发现:使用NN算法定位时,绝对距离的效果优于欧式距离;而使用KNN算法时,欧式距离的效果更加显著;不论选择哪个距离公式,使用KNN算法的定位效果都优于NN算法,图5(b)也可得出此结论。因而,使用NN算法计算绝对距离判断所属子库;使用KNN算法估计最终位置坐标,并令k=5达到较好的定位效果。
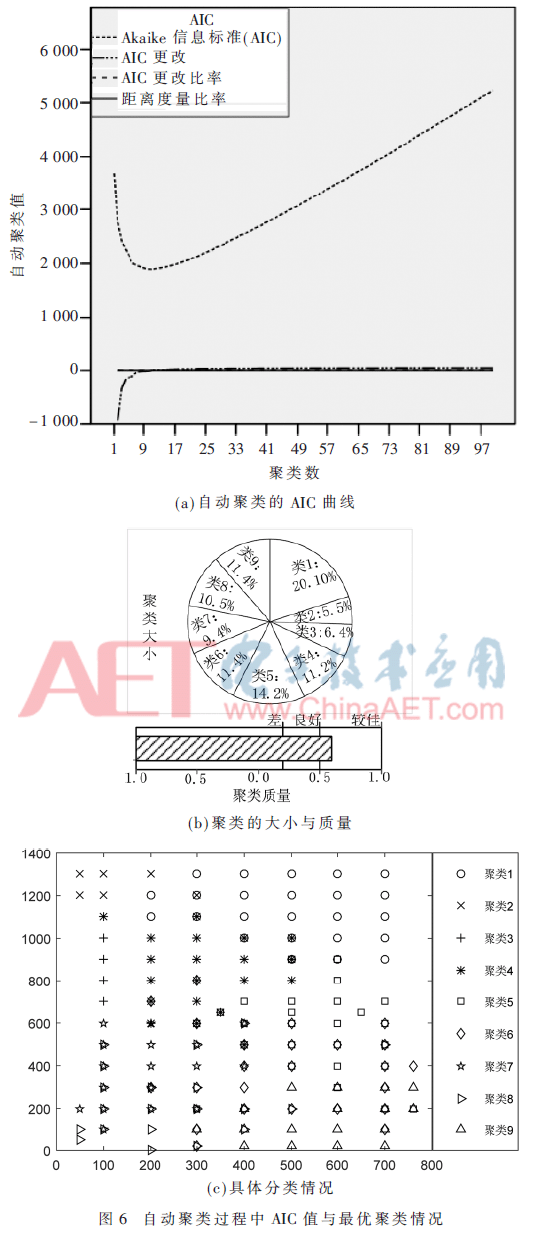
SPSS软件操作便捷、功能强大、运算速度快,直接使用该软件对指纹库RSSI进行两步聚类分析,根据AIC准则自动得到最优聚类个数与聚类分布情况。为排除所设聚类个数对结果的影响,设定最大聚类数目为100,自动聚类结果如图6所示。图6(a)显示出自动聚类过程中AIC值的变化情况:聚类效果的好坏并不随聚类数目的增加无限增长,而是呈凹曲线变化且最优的聚类个数较小。图6(b)显示出择优后的聚类情况:聚类数目为9,平均Silhouette为0.6,聚类质量良好且每类数目较均匀。图6(c)显示分类后每个类别的具体坐标值:同一位置的多个数据可能划分到不同类别,也验证了同一位置需在多个方向采集数据。
本文主要考证所提算法在定位精度与实时性方面有改善效果,因而选用定位效果较好的参数进行分析。即聚类个数为9,利用NN算法计算绝对距离判断所属子指纹库,使用k=5的KNN算法计算欧氏距离估计最终位置坐标。所提算法与KNN算法、K-means指纹定位进行比较,实验结果显示在表1中。

分析表1中数据可发现:(1)与传统指纹定位相比,聚类后的定位精度虽仅有较小幅度的改善,但运算时间缩短了37.84%~46.32%,即聚类处理后可显著提高定位的实时性。(2)确定聚类数目后,不论是用K-means还是两步聚类对数据进行聚类处理,最终的定位精度与实时性都相差无几,即聚类需预先得知最优的聚类个数。(3)所提算法与K-means指纹定位相比:虽然运算时间略有增加,但定位精度方面有小幅改善;且K-means指纹定位随机性大、稳定型差,而所提算法使用两步聚类依据AIC准则择优得到聚类数目,极大提高了算法的稳定性。综上述,本文所提算法相比当前已有算法在定位精度、实时性和稳定性方面都有一定的改善效果。
4 总结
本文通过蓝牙技术进行数据采集,针对K-means算法的定位精度较低、定位实时性差、聚类随机性导致稳定性差等问题,提出使用两步聚类根据AIC准则自动择优得到聚类数目,并使用相关系数法选择相似度最高的子指纹库来对其进行改进。实验结果表明:相关系数法可以有效提高算法的定位精度;两步聚类择优得到聚类个数后,可有效提高算法的稳定性和实时性。从整体来看,本文所提算法在定位精度、实时性和稳定性方面都有良好的改善。但本文仍有值得改进的地方,如已知聚类个数的情况下,本文所提算法是以时间为代价提高了定位精度与稳定性,接下来的工作中,需继续对其优化改进。
参考文献
[1] 田林青,余成波,孔庆达,等.基于蓝牙技术的推送系统的设计和实现[J].微型机与应用,2016,35(20):61-64.
[2] 陈空,宋春雷,陈家斌,等.基于改进WKNN的位置指纹室内定位算法[J].导航定位与授时,2016,3(4):58-64.
[3] CRAMARIUC A,HUTTUNEN H,LOHAN E S.Clustering benefits in mobile-centric WiFi positioning in multi-floor buildings[C].International Conference on Localization and Gnss.IEEE,2016.
[4] CUI Y,VOYLES R M.A mechanism for real-time decision making and system maintenance for resource constrained robotic systems through ReFrESH[J].Autonomous Robots,2015,39(4):487-502.
[5] LAITINEN E,LOHAN E S.On the choice of access point selection criterion and other position estimation characteristics for WLAN-based indoor positioning[J].Sensors,2016,16(5):737.
[6] 张杰,卓灵,朱韵攸.一种K-means聚类算法的改进与应用[J].电子技术应用,2015,41(1):125-128.
[7] 于睿,陆南.基于K均值聚类算法的位置指纹定位技术[J].信息技术,2015,39(10):185-188,191.
[8] 王艳丽,杨如民,余成波,等.相关性匹配蓝牙信标位置指纹库的室内定位[J].电讯技术,2017,57(2):145-150.
[9] TOBLER W R.A computer movie simulating urban growth in the Detroit region[J].Economic Geography,1970,46(Supp 1):234-240.
[10] 李奇.一种基于RSSI相关系数的指纹定位技术方法[J].广东通信技术,2013,33(3):29-32.
[11] AKAIKE H.Autoregressive model fitting for control[J].Annals of the Institute of Statistical Mathematics,1971,23(1):163-180.
[12] 秦宣云.基于AIC准则的最近邻聚类模型的优化算法[J].系统工程与电子技术,2005,27(2):257-259.
[13] 石欣,印爱民,陈曦.基于RSSI的多维标度室内定位算法[J].仪器仪表学报,2014,35(2):261-268.

