0 引言

    随着智能电网和电力系统的飞速发展，电力线载波通信(Power Line Communication，PLC)技术备受关注^[1-2]，然而电力线信道环境恶劣，传统单载波通信技术无法很好地抵御信道干扰，导致系统可靠性低，从而影响了电力线载波通信的应用和发展^[3]。G3-PLC标准是一种电力线载波通信规范，已经被IEEE、ITU和IEC/CENELEC等主要机构所采纳，可以有效地对输电网络、照明及智能电网应用进行管理、控制与监测^[4]，因此G3-PLC标准已成为面向智能电网通信技术的全球开放性协议^[5-6]。

    然而，OFDM系统的高频谱利用率和传输可靠性都是以其子载波之间的正交性为基础的，因此准确的符号定时同步技术是OFDM系统实现的关键。OFDM系统中的同步技术主要分两类：(1)利用循环前缀的方法；(2)利用训练序列的方法。当信道为严重的多径衰落信道时，第一类方法会使部分循环前缀区间受到ISI破坏，使定时估计性能恶化，因此不适用于电力线载波通信系统中。第二类方法主要用于如无线局域网(WLAN)的突发式传输系统，估计精度较高，在多径衰落信道下鲁棒性能较好，最具代表性的算法为Stanford大学的Schmidl和COX D C于1997年提出的Schmidl&Cox算法^[7]，但由于自相关平台效应，使S&C算法定时同步存在偏差。另一种经典的算法是Minn算法^[8]，虽然克服了S&C算法中符号定时测度的平台效应，但是其训练序列结构与G3-PLC标准的前导符号结构不相同，因此需要额外添加训练序列，使系统有效速率降低。

    因此，本文针对G3-PLC特有的前导符号结构，结合S&C算法的思想，提出了一种采用双重相关算法实现定时同步补偿的方法，并通过仿真对算法性能进行了验证。

1 G3-PLC信号帧结构

    一个完整G3-PLC的帧结构具体包括前导序列(Preamble)、帧控制头序列(Frame Control Header，FCH)以及数据位(DATA)。如图1所示，前导符号由8个SYNCP符号和1.5个SYNCM符号组成，其中每个SYNCP符号和SYNCM符号都包含256个采样点，同时，接收端为了方便进行相位检测，SYNCM符号相对于SYNCP符号有180°相位差。

    FCH帧控制头在前导符号之后，其包含了保证发送数据帧正确解调的必要信息。每一组数据帧中包含13个FCH符号，FCH之后是DATA数据信息，FCH本质上和数据位信息是一样的，因此其中也包含了循环前缀，但由于其重要性，导致其调制方式不可调，只可采用最安全的DBPSK调制映射方式，各个FCH数据段和DATA数据段在加窗之后需要进行相邻符号首尾重叠处理，重叠长度为8位。经过叠加之后，就形成了最后的数据帧。

2 双重相关检测同步原理

    SYNCP符号中有用的采样点码元由36个子载波的相位调制产生，其对应的36个相位信息如式(1)所示：

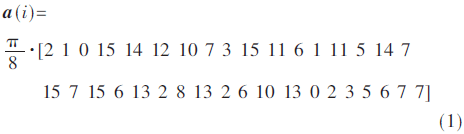
其中1≤i≤36表示有用载波序号。

    将式(1)中的各个相位值在频域建立对应的复数数据为：

    式(2)中的复数数据经过IFFT变换就可以产生前导序列中的一个SYNCP符号，为了使产生的SYNCP符号实数化，需对式(2)中的复数数据进行相应的频域编码，首先将式(2)中的36个复数数据位插入到N/2(其中N=256)个子载波中的第23～58位，其余位数补零，如式(3)所示：

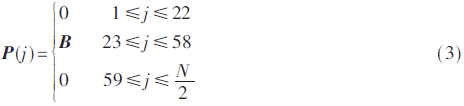
    再根据FFT原理，将式(3)形成的N/2个子载波P(j)按照式(4)映射到N个子载波的前N/2位，再将P(j)的第2～N/2位的共轭倒叙映射到N个子载波的后N/2-1位，第N/2+1位置零：

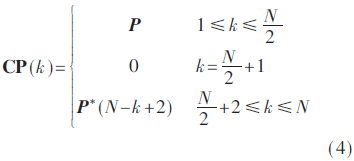
    再对该N个信息数据进行N点IFFT变换，得到的SYNCP符号如下式，即为实数序列：

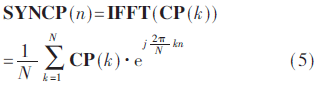
其中，0≤n≤N-1。

    SYNCM码元是由P码元反相产生的，如式(6)所示：

    在接收端，根据信道环境，在本地倒序选取一定长度的前导符号序列，假设接收端本地前导符号序列长度为发送端前导符号序列长度的1/2，即：

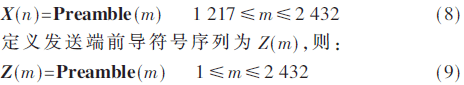
    定义接收端经过信道干扰的产生失步的信息帧为Y(m)，截取接收到的信息帧的前2 432位。

    根据相关检测原理，分别将Z(m)与X(n)和Y(m)与X(n)进行滑动互相关运算，即：

    接收端通过对失步量进行补偿即可精确地确定出每一帧信息中FCH位及DATA位的起始时刻。

3 系统性能验证

    为了验证本文基于前导的G3-PLC同步算法性能，采用Monte Carlo方法对系统进行仿真验证，结果如图2所示，其中仿真参数设置为：子载波数目N=256，保护间隔的长度为CP=30，采样频域F_S=0.4 MHz，SNR=-2 dB，符号偏差为399个载波符号周期，FCH符号数为N_FCH=13，数据位采用DQPSK调制方式，FCH位采用DBPSK调制方式。图2(a)为R_ZX(m)相关曲线，由图可以得出J₁=3 456；图2(b)为R_YX(m)相关曲线，其中J₂=3 058，得D=J₁-J₂=398，与符号偏差值399差一个载波符号周期，在接收端通过补偿即可判断出正确的FCH位及DATA位的起始位置。

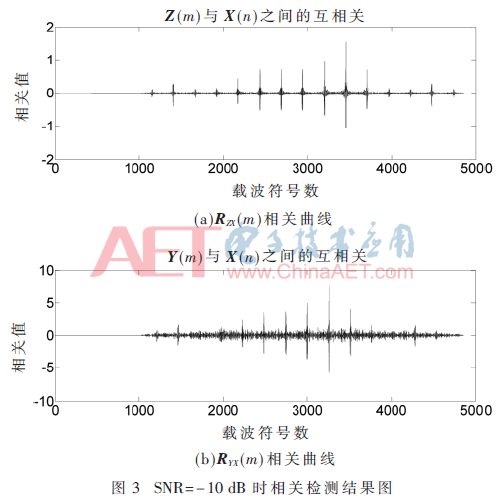
    其他参数SNR=-10 dB保持不变，恶化信道环境设置，符号偏差为200个载波符号周期。图3(a)为R_ZX(m)相关曲线，由图可以得出J₁=3 456；图3(b)为R_YX(m)相关曲线，其中J₂=3 257，得D=J₁-J₂=199，与符号偏差值200同样只差一个载波符号周期，在接收端通过补偿即可判断出正确的FCH位及DATA位的起始位置。

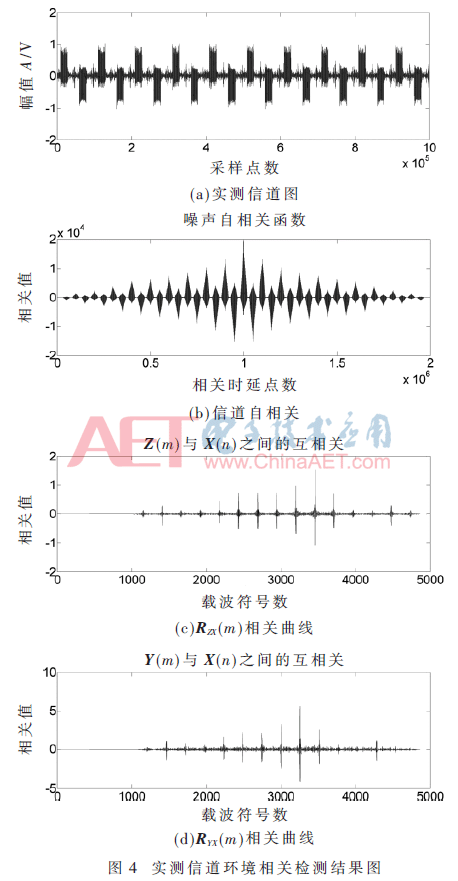
    为了进一步验证该算法对信道环境的适应性，其他参数保持不变，符号偏差为200载波符号周期,采用电力线载波实测信道参数环境，如图4(a)所示为实测信道时域图，由于电力线载波实际信道自相关曲线具有周期对称性，如图4(b)所示，因此其自相关程度近似为零，信号通过该信道后其相关性不会受到太大影响；图4(c)为R_ZX(m)相关曲线，由图可以得出J₁=3 456；图4(d)为R_YX(m)相关曲线，其中J₂=3 257，得D=J₁-J₂=199，与符号偏差值200同样只差一个载波符号周期，在接收端通过补偿即可判断出正确的FCH位及DATA位的起始位置。

4 结论

    由于低压电力线建设初期并没有考虑通信的要求，因此在传输信号过程中会受到噪声、多径干扰和频率选择性衰落等影响，造成定时同步不准确，在接收端产生漏检和误判。本文首先解析了G3-PLC电力线载波通信原理及G3-PLC信号帧结构，并根据G3-PLC电力线通信协议特有的帧格式，利用前导序列之间的相关性，提出采用两重相关的检测方法对系统的失步进行了有效的补偿，并且最后通过Monte Carlo方法对系统进行了仿真验证。结果表明，本文提出的系统同步补偿算法对不同信道环境适应性好，可以准确地检测到FCH位及DATA位的起始位置，使接收端能够正确地解调信息，算法实现简单，可靠性高。

参考文献

[1] 辛耀中，石俊杰，周京阳，等.智能电网调度控制系统现状与技术展望[J].电力系统自动化，2015，39(1)：2-8.

[2] 王继业，马士聪，仝杰，等.中日韩电网关键技术发展及趋势分析[J].电网技术，2016，40(2)：491-499.

[3] RAZAZIAN K，UMARI M，KAMALIZAD A，et al.G3-PLC specification for powerline communication：overview，system simulation and field trial results[C].IEEE International Symposium on Power Line Communications & Its Applications.Brazil，2010：313-318.

[4] HOCH M.Comparison of PLC_G3 and PRIME[C].IEEE International Symposium on Power Line Communication and Its Application.Udine，2011：165-169．

[5] SOUISSI S，DHIA A B，TLILI F，et al.OFDM modem design and implementation for narrowband Powerline communication[C].International Conference on Design & Technology of Integrated Systems in Nanoscale Era，Hammamet，tunisia，2010：1-4.

[6] 李春阳，黑勇，乔树山.OFDM电力线载波通信系统的定时同步和模式识别[J].电力系统自动化，2012，36(8)：58-60.

[7] SCHMIDL T M，COX D C.Robust frequency and timing synchronization for OFDM[J].IEEE Transactions on Communications，1997，45(12)：1613-1621.

[8] MINN H，ZENG M，BHARGAVA V K.On timing offset estimation for OFDM systems[J].IEEE Communications letters，2000，4(7)：242-244.