文献标识码: A
DOI:10.16157/j.issn.0258-7998.172989
中文引用格式: 董志翔,赵宜升,黄锦锦,等. 基于支持向量机的高速铁路通信系统信道预测算法[J].电子技术应用,2018,44(4):117-121.
英文引用格式: Dong Zhixiang,Zhao Yisheng,Huang Jinjin,et al. Support vector machine for channel prediction in high-speed railway communication systems[J]. Application of Electronic Technique,2018,44(4):117-121.
0 引言
在自适应调制编码过程中,如何高精度地获取信道状态信息是关键。在频分双工通信系统中,通过信道估计虽然可以得到信道状态信息,但由于存在反馈和处理时延,获取的信道状态信息已经过时,不能反映发送时刻的信道状况。信道预测可以根据过时的信道状态信息,预测未来发送时刻的信道状况,能够显著提高自适应调制编码的准确性。
信道预测问题已经引起了广泛的关注。一类信道预测算法是线性预测算法,比较成熟的算法主要是自回归(Autoregressive,AR)模型。针对瑞利衰落信道,文献[1]采用二阶AR模型进行信道预测。然而,对于具有非线性特性的快速时变信道,线性预测并不适用。另一类信道预测策略是非线性预测方案[2],其中一种是基于神经网络[3]的信道预测方法,但是神经网络无法克服过拟合和局部最小问题。因此,另一种基于支持向量机[4](Support Vector Machine,SVM)的信道预测方法受到重视。SVM是一种基于结构风险最小化原则的机器学习算法,通过映射至高维空间解决非线性问题[5]。该方法结构简单,数据处理能力强大,适用于预测快速时变信道[6]。然而,预测性能和复杂度受SVM模型中的惩罚系数和高斯核宽度影响,需要进行进一步优化。
本文采用SVM研究高速铁路通信系统的信道预测问题。首先,将信道数据分为训练集和测试集。然后,使用训练集,依据SVM理论求解最优超平面。采用对偶变化将原问题转为求解方程组的解,通过循环迭代实现多步预测。为了提升预测性能和降低复杂度,引入遗传算法(Genetic Algorithm,GA),对SVM模型中的惩罚系数和高斯核宽度进行优化。最后,根据测试集,对不同条件下的预测误差进行评估。同时,以归一化均方误差(Normalized Mean Squared Error,NMSE)作为性能参数,对预测值与实际值的拟合效果进行评价。
1 系统模型
1.1 网络结构
高速铁路通信系统的网络结构如图1所示,它主要由地面子系统和车载子系统组成。地面子系统包含基站(Base Station,BS)和远端天线单元(Remote Antenna Unit,RAU)[7]。BS为信号源,RAU在铁路沿线上灵活部署。多个RAU通过光纤分别连接到BS,可以扩大信号的覆盖区域。BS和RAU分别用于处理基带信号与射频信号,从BS发射的基带信号以光纤传输到RAU[8]。对于车载子系统,在列车的顶部安装一个车载台(Vehicular Station,VS),可以克服车体穿透损耗。同时,在每节车厢安装一个中继器(Repeater,R),R和VS通过有线方式连接。不同的用户设备(User Equipment,UE)以无线方式通过中继器接入网络。
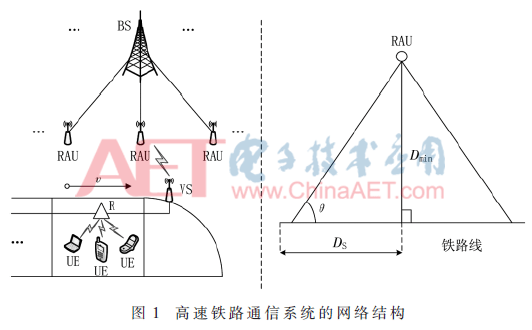
1.2 信道模型
对于高速铁路通信系统,接收端接收到的信号是由一条视距(Line-of-Sight,LOS)信号和多条多径效应产生的非视距(Non Line-of-Sight,NLOS)信号的叠加。此时接收信号的包络服从莱斯分布。RAU和VS之间的信道冲激响应为[9]:

其中,v表示列车的移动速度,c表示电磁波的传播速度,fc是载波频率。式(2)中θ为LOS分量到达时的角度,cosθ的值可以通过下式计算:
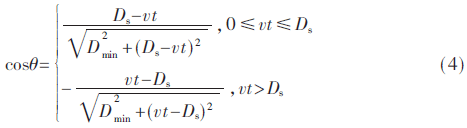
其中,Ds为铁路线方向上列车与RAU之间的初始距离,Dmin是RAU和铁路线之间的距离。
2 信道预测算法
2.1 支持向量机
本小节将介绍SVM的基本原理。SVM理论的切入点是,找出线性可分点集间的判决超平面,它的表达式为:

其中,K(·)为核函数[12]。由于简单地将低维空间映射至高维,会引起维度灾难。通过将高维空间的内积运算转为低维空间的核函数计算,可以避免维度灾难,极大地降低运算量。本文采用径向基函数作为核函数:

其中,σ是高斯核的宽度,在映射到新特性空间后,其隐式地确定支持向量的分布区间范围[13]。
参数C和σ影响SVM模型的学习能力。本文采用k折交叉验证(k-fold cross-validation,k-cv)优化这两个参数,即分别训练k组预测模型最后取平均误差作为总体性能。不失一般性,选择k=3。
2.2 遗传算法优化寻优
用启发式算法就可以不必遍历所有的参数点,从而得到和上述方法一样甚至更优的预测模型。本文采用GA改进参数寻优,将改进后的SVM模型表示为SVM-GA。遗传算法是一种通过模拟自然进化过程搜索最优解的方法,从代表问题可能潜在解集的一个种群开始,按照适者生存和优胜劣汰的原理,逐代演化产生出近似解。在每一代,根据问题域中个体的适应度选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新解集的种群[14]。具体流程如图2所示。
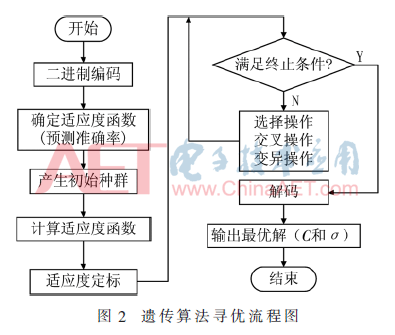
具体来说,本文是对C和σ进行寻优。首先对C和σ进行二进制编码,将其表示成遗传空间中由基因按一定结构组成的染色体。二进制编码是指由二进制字符集{0,1}产生0和1字符串来表示问题空间的候选解。进化论中的适应度是表示某一个体对环境的适应能力,也表示该个体繁殖后代的能力。遗传算法的适应度函数也叫评价函数,是用来判断群体中的个体的优劣程度的指标,它是根据所求问题的目标函数来进行评估的。本文采用cv意义下的预测准确率作为适应度函数值。当种群迭代次数达到设计的上限时,跳出循环,解码输出最优解,否则执行选择、交叉和变异3个基本遗传算子:
(1)选择:从群体中选择优胜的个体,淘汰劣质个体的操作。
(2)交叉:把两个父代个体的部分结构加以替换重组而生成新个体的操作。
(3)变异:对群体中的个体串的某些基因座上的基因值作变动。
2.3 预测算法设计
本节将给出基于SVM的信道预测算法的具体执行过程。基于SVM的高速铁路通信系统信道预测算法具体步骤如下:
(1)由式(1)所示的高速铁路通信系统信道模型,产生一组信道冲激响应序列。假设采样间隔为TS,可以得到500个信道冲激响应的采样值:h(TS),h(2TS),…,h(500TS)。
(2)将500个数据的实部和虚部分开处理。将实部表示为Re(TS),Re(2TS),…,Re(500TS)。同理,将虚部表示为Im(TS),Im(2TS),…,Im(500TS)。选择前400个作为训练集,剩下的100个作为测试集。
(3)将实部的训练集代入式(11),得到实部的拉格朗日乘子和预测模型。根据k-cv以及遗传算法,计算对应的C和σ。同理可得虚部的预测模型。
(4)根据超平面的表达式写出预测值,实部和虚部分别表示如下:

3 仿真结果和分析

图3显示了不同训练样本个数对基于SVM的信道预测算法预测误差的影响。预测目标均为测试集数据,训练数据分别选取如下:当选取200个训练样本时,选取其中{201,202,…,400}采样点数据作为训练集;当选取300个训练样本时,选取其中{101,102,…,400}采样点数据作为训练集;当选取400个训练样本时,选取训练集整体数据作为训练集。可以发现,由400个训练样本所得到预测模型最精确。此外,200个训练样本出现了明显欠拟合的情况,其原因是需要足够的数据来进行训练以获取能完整表述出预测模型的支持向量。在后续的仿真中,训练样本个数都设置为400。

图4给出了在不同最大进化代数情况下, SVM-GA算法在各个采样点的预测误差。在仿真时,没有考虑噪声的影响。可以看到,在进化代数更高时,预测的准确度越高。然而,进化次数并不是越高越好。因为采用遗传算法优化的主要目的还是减少训练时间,而迭代次数越大,算法的复杂度越高,反而会延长训练时间。在真实情况中,应该平衡实际需求和优化目标二者间的关系,在预测精度变化不大的前提下,可以适当牺牲准确度以提高预测效率。在后续的仿真中,进化代数都设置为200。

图5对比了AR、SVM和SVM-GA 3种预测模型在各个采样点的预测误差。在仿真时,没有考虑噪声的干扰。可以看出,SVM比AR具有更小的预测误差。这是因为在训练后产生的支持向量在预测中起着决定性的作用,在处理异常值时,使得SVM比AR更健壮。此外,SVM-GA的预测准确性也比SVM略高,这是因为经过遗传算法筛选寻优得到的参数C和σ比一般的网格寻优更能体现出整体预测模型的性质,所以其对预测目标的拟合程度也比不经过遗传算法改进的更高。

图6对比了AR、SVM和SVM-GA 3种不同预测模型在不同噪声功率下的NMSE。NMSE定义如下;

其中,Q是预测数据的总个数。在仿真中,参数Q的值设置为100。可以观察到,随着噪声功率的增大,3种模型的NMSE都在增加。同时,SVM模型的NMSE比AR模型的小得多,而SVM-GA模型的效果比这二者效果都好。因此,SVM-GA模型的信道预测方法在实际场景中具有更好的性能。

4 结论
本文研究了高速铁路通信系统的信道预测问题。根据SVM理论,通过求解二次优化问题和循环迭代,实现多步预测。此外,通过引入GA,对SVM模型中的惩罚系数和高斯核宽度进行优化处理。仿真结果显示,在预测误差和NMSE方面,本文提出的SVM-GA改进模型比AR模型以及单一的SVM模型具有更好的性能。在未来的工作中,将考虑回声状态网络(Echo State Network,ESN)预测模型,对信道预测问题进行进一步研究。
参考文献
[1] SHARMA P,CHANDRA K.Prediction of state transitions in Rayleigh fading channels[J].IEEE Transactions on Vehicular Technology,2007,56(2):416-425.
[2] 孙建成,张太镒,刘枫.一种新的快速衰落信道非线性预测算法[J].北京航空航天大学学报,2005,31(5):499-503.
[3] DING T,HIROSE A.Fading channel prediction based on combination of complex-valued neural networks and chirp z-transform[J].IEEE Transactions on Neural Networks and Learning Systems,2014,25(9):1686-1695.
[4] 相征,张太镒,孙建成.基于最小二乘支持向量机的衰落信道预测算法[J].电子与信息学报,2006,28(4):671-674.
[5] JIANG J,LI J.Modification of SVM’s optimal hyperplane based on minimal mistake[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(11):1483-1486.
[6] CHU W,CHONG J O,KEERTHI S S.An improved conjugate gradient scheme to the solution of least squares SVM[J].IEEE Transactions on Neural Networks,2005,16(2):498-501.
[7] WANG H H,HOU H A,CHEN J C.Design and analysis of an antenna control mechanism for time division duplexing distributed antenna systems over high-speed rail communications[J].IEEE Transactions on Emerging Topics in Computing,2016,4(4):516-527.
[8] ZHAO Y S,JI H,CHEN Z H.Admission control scheme for handover service in high-speed train communication system[J].Journal of Shanghai Jiaotong University(Science),2015,20(6):670-675.
[9] CHEN Y,BEAULIEU N C.Estimation of Ricean K parameter and local average SNR from noisy correlated channel samples[J].IEEE Transactions on Wireless Communications,2007,6(2):640-648.
[10] ZHANG Y,CHAI T,WANG D.An alternating identification algorithm for a class of nonlinear dynamical systems[J].IEEE Transactions on Neural Networks and Learning Systems,2017,28(7):1606-1617.
[11] YOON H,HYUN Y,HA K,et al.A method to improve the stability and accuracy of ANN- and SVM-based time series models for long-term groundwater level predictions[J].Computers and Geosciences,2016,90(PA):144-155.
[12] ELANGOVAN M,SUGUMARAN V,RAMACHANDRAN K I,et al.Effect of SVM kernel functions on classification of vibration signals of a single point cutting tool[J].Expert Systems with Applications,2011,38(12):15202-15207.
[13] DANTI A,SURESHA M.Arecanut grading based on three sigma controls and SVM[C].IEEE International Conference on Advances in Engineering,Science and Management,2012:372-376.
[14] 袁晓辉,袁艳斌,王乘,等.一种新型的自适应混沌遗传算法[J].电子学报,2006,34(4):708-712.
[15] CHANG C C,LIN C J.LIBSVM——A library for support vector machines[EB/OL].(2016-12-22)[2017-07-05].http://www.csie.ntu.edu.tw/~cjlin/libsvm/index.html.
作者信息:
董志翔,赵宜升,黄锦锦,陈梦嘉,陈忠辉
(福州大学 物理与信息工程学院,福建 福州350116)

