《电子技术应用》
您所在的位置：首页 > 测试测量 > 设计应用 > 概率神经网络多模型卡尔曼滤波定位导航算法
概率神经网络多模型卡尔曼滤波定位导航算法
2018年电子技术应用第6期
梁龙凯1，2，张丽英1，何文超1，2，吕绪浩1，2
1.东北师范大学 人文学院 理工学院 汽车电子与服务工程系，吉林 长春130117； 2.吉林省高校汽车电子技术工程研究中心，吉林 长春130117
摘要： 交互式多模型扩展卡尔曼滤波（IMM-EKF）算法是解决机动载体运动模型不确定的定位问题的次优算法，在载体做模型确定的运动时该方法仍得到次优解且浪费运算资源。针对IMM-EKF算法的此类缺陷，采用离线训练的概率神经网络模型，实时判断当前运动模型分类，在运动模型确定的状态下选择对应的单一模型进行运算，而在运动模型不确定的状态下选择IMM-EKF算法，既保证定位精度，又减少了不必要的运算量。仿真对比实验验证了相比于IMM-EKF算法，新算法在精度方面的优势。
中图分类号： TP29
文献标识码： A
DOI：10.16157/j.issn.0258-7998.174938
中文引用格式： 梁龙凯，张丽英，何文超，等. 概率神经网络多模型卡尔曼滤波定位导航算法[J].电子技术应用，2018，44(6)：60-62，67.
英文引用格式： Liang Longkai，Zhang Liying，He Wenchao，et al. Probabilistic neural network multi-model Kalman filter navigation algorithm[J]. Application of Electronic Technique，2018，44(6)：60-62，67.
Probabilistic neural network multi-model Kalman filter navigation algorithm
Liang Longkai1，2，Zhang Liying1，He Wenchao1，2，Lv Xuhao1，2
1.Automotive Electronics and Services Engineering Department，College of Humanities & Sciences of Northeast Normal University， Changchun 130117，China； 2.Jilin Provincial University Automotive Electronic Technology Engineering Research Center，Changchun 130117，China
Abstract： Interacting multiple model extended Kalman filter(IMM-EKF) algorithm is a sub-optimal algorithm which can solve the positioning problem in which the motion model is uncertain. But this method still gets sub-optimal solution and wastes computational resources when the carrier does the motion of which the model is certain. Aiming at this kind of defects of IMM-EKF, the off-line training probabilistic neural network model is adopted to judge the classification of current motion model in real time. We choose to operate with the single corresponding model when the motion model is in the state of certainty, and choose the IMM-EKF algorithm when the motion model is in the uncertain state. Thus it not only ensures the positioning accuracy, but also reduces the unnecessary computation burden. Simulation experiments verify the validity and accuracy of the algorithm, while the contrast test verifies the advantages in accuracy of the new algorithm compared with IMM-EKF algorithm.
Key words : navigation；extend Kalman filter(EKF)；probabilistic neural network(PNN)；BDS；GPS

0 引言

    扩展卡尔曼滤波(Extend Kalman Filter，EKF)需要一个准确的运动模型，如果运动载体的运动状态不确定，则扩展卡尔曼滤波的估计偏差将会很大甚至估计失败。针对这种模型不确定的情况，BLOM H和BAR-SHALOM Y于1988年提出了交互式多模型(Interacting Multiple Model，IMM)的次优算法[1]。因此采用交互式多模型扩展卡尔曼滤波(Interacting Multiple Model- Extend Kalman Filter，IMM-EKF)算法可实现运动模型不确定的非线性系统运动载体的卫星定位。

    然而IMM-EKF在计算过程中需要计算模型集中所有模型的卡尔曼滤波结果，运算量随模型集规模增加[2]，即使在运动载体的运动状态符合模型集中的某一模型的情况下，依然要进行其他模型的计算，且得到次优的估计结果[3]。

    针对上述不足，本文引入概率神经网络(PNN)算法，通过离线训练好的神经网络模型对运动状态进行分类，若运动状态与模型集中某模型类型匹配，则采用单一模型进行EKF得到最优估计；若运动状态与模型集中任何模型分类都不匹配，则采用IMM-EKF定位。

1 扩展卡尔曼滤波（EKF）

    离散非线性系统的状态空间描述为[4]：

ck3-gs1-7.gif

2 GPS/BDS系统滤波模型的建立

    选取GPS/BDS系统的状态变量为[5]：

ck3-gs8-9.gif

式中Wk-1为k-1时刻的系统过程噪声，是零均值的高斯白噪声[6]。式中Φ的具体表达形式取决于运动模型的形式[7]，运动模型可参考文献[5]和[7]中提到的模型。

3 交互式多模型卡尔曼滤波

ck3-gs10.gif

    ck3-gs11.gif

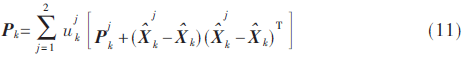
4 引入反馈的概率神经网络（BP-PNN）

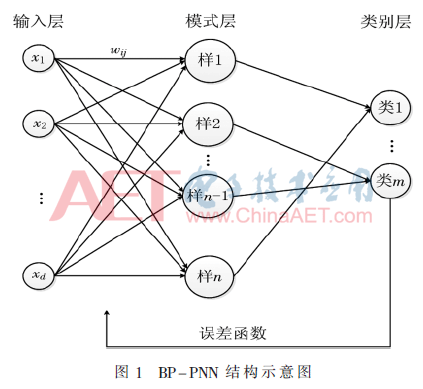
    概率神经网络是由SPECHT D F于1990年提出的，用于解决模式分类及决策问题[8]。李永立等人在此基础上提出了引入反向传播机制的概率神经网络[9]，使概率神经网络模型的空间开销减小，分类精度提高。BP-PNN结构如图1所示，算法如下。

ck3-t1.gif

ck3-gs12-17.gif

5 仿真

    运动轨迹分4个阶段，分别采用不同的运动状态，各运动状态可遵循不同的状态模型，具体运动轨迹如表1所示。

ck3-b1.gif

5.1 实验1：概率神经网络的离线学习、训练

    在表1的数据中分别提取第一阶段“匀速转弯”前3 s的数据和第三阶段“匀加速直线”前3 s的数据，将第一阶段数据目标归类定义为1；将第三阶段数据目标归类定义为2；其他两个阶段各提取前3 s数据，目标归类定义为3。利用各阶段前3 s的数据进行概率神经网络学习，再利用各阶段4～6 s数据进行概率神经网络训练。采用任意轨迹数据进行测试，仿真结果显示如表2所示。

ck3-b2.gif

    实验结果表明经过概率神经网络的离线训练，可以比较精确地对输入数据进行分类，尤其是匀加速直线运动的分类准确率最高。

5.2 实验2：PNN-EKF的准确性实验

ck3-5.2-x1.gif

    仿真结果如图2所示。

ck3-t2.gif

    从仿真结果可以看出PNN-EKF的定位精度要高于IMM-EKF，但在x轴方向起始阶段由于概率神经网络对状态判断不准确造成一定程度的偏差，后续阶段及y轴整体精度都优于IMM-EKF。

6 结束语

    本文提出一种利用概率神经网络判断运动状态,进而采用对应模型进行EKF的GPS/BDS导航定位算法。该算法当概率神经网络能够判断其对应运动模型时，采用单一模型进行最优解计算，如不能判断准确模型则归类为“其他”，“其他”类的数据采用IMM-EKF算法。这样就可以在多数情况下求得最优解，从而提高精度。通过仿真实验证明相较于IMM-EKF，本文算法定位精度有所提高，从理论推导中可以判断本文算法当模型集较大时运算时间会有所减少。

参考文献

[1] 翟岱亮，雷虎民，李炯，等.基于自适应IMM的高超声速飞行器轨迹预测[J].航空学报，2016，37(11)：3466-3475.

[2] 董宁，徐玉娇，刘向东.一种带自适应因子的IMM-UKF的GPS/DB-2导航方[J].宇航学报，2015，36（6）：676-683.

[3] 苗少帅，周峰.IMM迭代无迹Kalman粒子滤波目标跟踪算法[J].重庆邮电大学学报(自然科学版)，2015，27(1)：44-48.

[4] 吴甜甜，张云，刘永明，等.北斗/GPS组合定位方法[J].遥感学报，2014，18(5)：1087-1097.

[5] 徐玉娇.GPS/BD-2组合导航系统定位算法的研究[D].北京：北京理工大学，2015.

[6] MONTENBRUCK O，HAUSCHILD A，STEIGENBERGER P，et al.Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system[J].GPS Solutions，2013，17(2)：211-222.

[7] ZHOU H R，KUMAR K S P.A ‘current’ statistical model and adaptive algorithm for estimating maneuvering targets[J].Journal of Guidance，Control，and Dynamics，1984，7(5)：596-602.

[8] SPECHT D F.Probabilistic neural networks[J].Neural Networks，1990，3(1)：109-118.

[9] 李永立，吴冲，罗鹏.引入反向传播机制的概率神经网络模型[J].系统工程理论与实践，2014，34（11）：2921-2928.

[10] 苑津莎，尚海昆.基于主成分分析和概率神经网络的变压器局部放电模式识别[J].电力自动化设备，2013，33(6)：27-31.

[11] MICHAEL R B，JAY D.Constructive training of probabilistic neural networks[J].Neurocomputing，1998，19(1-3)：167-183.



作者信息:

梁龙凯1，2，张丽英1，何文超1，2，吕绪浩1，2

（1.东北师范大学 人文学院 理工学院 汽车电子与服务工程系，吉林 长春130117；

2.吉林省高校汽车电子技术工程研究中心，吉林 长春130117）

此内容为AET网站原创，未经授权禁止转载。

相关内容