文献标识码: A
DOI:10.16157/j.issn.0258-7998.174144
中文引用格式: 吴鹏,周杰,陈姜高路,等. 礼堂直达与非直达传播环境建模及性能研究[J].电子技术应用,2018,44(6):103-107.
英文引用格式: Wu Peng,Zhou Jie,Chen Jianggaolu,et al. Modeling and performance study of direct and indirect radio propagation environment in auditorium[J]. Application of Electronic Technique,2018,44(6):103-107.
0 引言
在无线传播环境中,由于信号可能遇到环境内的障碍物引起的反射、散射以及衍射,从各个方向传播到接收端的电磁信号路径各异。在过去的研究中常采用大量的测量方法并且得到了一些基于经验的统计模型[1-3]。然而这些模型只能在信道特性相同的环境中运用,否则产生误差较大。射线追踪法常被应用于随机信道的建模,射线传播遇到散射体时,根据衍射理论检测每一条路径获取该路径的信息[4],但这种方法建立模型依赖于传播环境结构及散射体的具体分布。因此,研究人员又提出集合散射模型,最初提出一个简单的环散射模型[5-6],之后根据该模型提出了双环散射模型[7-8]。此外,有研究人员通过放置一系列点散射体用于分析公路上车辆之间的信道[9],且其他研究人员将该方法用于模拟浅水区声音传播信道[10]。在建立理论模型时为降低复杂度,通常假设散射体服从均匀分布[6-10],以往的研究结果也表明均匀散射体分布模型能较好地拟合多种天线传播环境。上述文献中均假设空间对称分布,但对于内部结构不规则以及散射体性质区别极大的环境,都可能使得通信系统呈现出非对称性。为降低计算量并获得闭合的函数表达式,本文假设散射体均匀分布,其中接收端(Receiver,Rx)和发送端(Transmit,Tx)任意放置,不仅考虑到直达(Line Of Sight,LOS)散射,并将非直达(No Line Of Sight,NLOS)散射作为本文的特殊情况。此外,本文根据参考模型提出用于仿真的SOC(Sum Of Cisoids)信道模型,应用等面积几何算法(Generalized Method of Equal Areas,GMEA)和基本黎曼和方法(Basic Riemann Sum Method,BRSM)参数化SOC信道仿真模型,并以多普勒功率谱密度(Power Spectral Density,PSD)和时间自相关函数(Auto Correlation Function,ACF)为指标将二者的性能进行比较。
1 礼堂信道散射模型
如图1所示,通常礼堂由最后排观众席到主席台两侧的宽度逐渐变窄,外形近似为等腰梯形,将其竖直投影到二维水平面上,得到如图2所示的几何模型,实心黑点表示散射体,A和a分别表示此等腰梯形水平面的下底和上底长,h为等腰梯形的高。Tx和Rx在梯形内的任意位置,取梯形中心位置(即该梯形中位线的中点处)为坐标原点O,Rx沿着x轴匀速运动。假设NLOS信号只发生单次反射以及图2散射区域内所有的散射体均为全向辐射且无反射损耗。

2 信道参数及统计特征
2.1 信道参考模型
本文通过如下方程对非频率选择性衰落信道建立模型:


2.2 AOA概率密度函数
本文假设在坐标系用(x,y)表示散射体的位置,图2中O的坐标为(m,n),为了便于分析,将O移动到Rx处,新坐标系如图3所示,有x′=x-m,y′=y-n。由于Tx的位置对参考模型的统计特性无任何影响,因此图3中没有标出Tx的位置。

图3中达波信号的到达角度(Angle of Arrival,AOA)θ可表示:


2.3 多普勒Doppler PSD


3.1 计算方法
本文分别采用了GMEA和BRSM计算SOC仿真模型的参数ci、fi。根据GMEA方法,信道增益ci为:

3.2 SOC信道统计特征

4 数值结果与分析
本文假设梯形上底长a=20 m,下底长A=40 m,梯形的高h=40 m,其余参数设置为:fρ=60 Hz,σ2=1,φρ=0°,fmax=90 Hz,莱斯因子分别取0、3、6,SOC仿真模型中设置样本函数的个数I的值为20,取m=2,n=3。由图4可知,AOA的PDF在一定范围内单调递减或递增,且无论信道为宽带或窄带,AOA的PDF都相同。

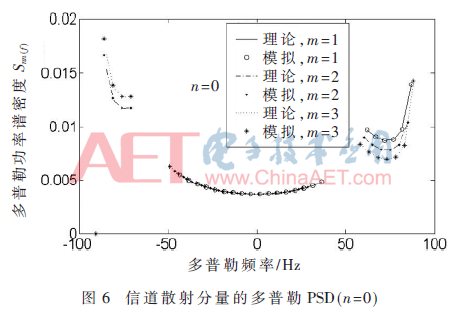
图5和图6表示根据式(18)仿真出信道散射分量n(t)的多普勒功率密度Snn(f),二者分别选定两个不同的Rx的位置(即分别改变m和n的值),由图可知,当多普勒频率增加时,其PSD也随之增加。图5表示出当m=0时,n(t)的Snn(f)为频率相关且对称[14]。而在图6中令n=0,情况有所改变。根据图5还可看出当m=0,在改变n的值的情况下,在|f|逼近±fmax时二者值相等。因此,可以得到结论:|f|逼近±fmax时,多普勒PSD与n的值无关,仅仅由m的取值决定[14]。

如图7所示,仿真模型选取不同的A的值,并研究其对散射分量Snn(f)的影响。由图可知,增大A的值,PSD的图形越来越趋向于完整的字母U的形状。在多普勒频率|f|逼近±fmax时,多普勒PSDSnn(f)随着频率的增加而增加。
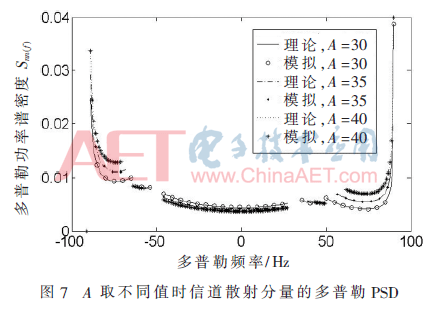
图8和图9分别表示在n(t)的多普勒PSDSnn(f)对称的情况下(取m=0,n=5),将GMEA和BRSM设计的SOC仿真模型与参考模型的时间ACF对比。由图可知,SOC仿真信道模型与参考模型在时间延迟较小时几乎重合。对比图8与图9,可以看出采用BRSM计算参数的SOC仿真信道模型与参考模型相匹配的时间延迟范围要大于GMEA。因此,在计算信道模型时间ACF方面,BRSM的性能优于GMEA。


图10和11分别表示在多普勒PSDSnn(f)非对称的情况下(m=2,n=0),采用GMEA和BRSM的SOC信道仿真模型的时间ACF与参考模型的对比。由图可知,SOC信道仿真模型在一定的时延内与参考模型较为吻合。此外,再次将GMEA与BRSM设计的SOC仿真信道对比可知,BRSM方法在与参考模型相匹配的时间延迟范围方面要大于前者。因此,计算信道模型ACF时,BRSM的SOC仿真模型的性能更好。


5 结论
本文针对典型的礼堂无线传播环境中信号传播的LOS与NLOS情况,提出基于几何的散射模型并改进得到参考模型。假设散射体在散射区域内均匀分布,推导出波达信号AOA的PDF、多普勒PSD以及时间ACF的表达式,并分析主要参数对信道模型统计特性的影响。此外,本文根据参考模型设计出SOC仿真模型以及BRSM和GMEA两种方法用于参数化仿真模型。结果表明,BRSM和GMEA都是计算模型参数高效准确的方法,仿真模型均与对应参考模型中的在统计特性方面较好匹配,而在时间ACF方面BRSM在一定程度上优于GMEA。文中的结论不但对于室内无线通信性能评估具有重要意义,且拓宽了高效仿真信道模型的研究。
参考文献
[1] BAPTISTA A,HOWE B,FREIRE J,et al.Scientific exploration in the era of ocean observatories[J].IEEE Computing in Science Engineering,2008,10(3):53-58.
[2] RASHID M T,ALI A A,ALI R S,et al.Wireless underwater mobile robot system based on ZigBee[M].New York:ICFCN,2012.
[3] DALBRO M.Wireless sensor networks for off-shore oil and gas installations[M].London:SENSORCOMM,2008.
[4] SHIN D,NA S Y,KIM J,et al.Fish robots for water pollution monitoring using ubiquitous sensor networks with sonar localization[M].New York:ICCIT,2007.
[5] CHITRE M.A high-frequency warm shallow water acoustic communications channel model and measurements[J].Journal of Acoustical Society America,2007,122(5):2580-2586.
[6] BREKHOVSKIKH L M,LYSANOV Y P.Fundamentals of ocean acoustics[M].New York:Springer,2002.
[7] STOJANOVIC M.Underwater acoustic communications:design considerations on the physical layer[M].London:5th Annu Conf Wireless Demand Netw Syst Services,2008.
[8] DOMINGO M C.Overview of channel models for underwater wireless communication networks[J].Physical Communication,2008,1(3):163-182.
[9] BOUVET P G,LOUSSERT A.Capacity analysis of under-water acoustic MIMO communications[M].Sydney:IEEE OCEANS,2010.
[10] HICHERI R,P?魧TZOLD M,TALHA B,et al.A study on the distribution of the envelope and the capacity of underwater acoustic channels[M].Macau.:IEEE International Conference on Communication Systems(ICCS),2014.
[11] TEAL P D,ABHAYAPALA T D,KENNEDY R A.Spatial correlation in non-isotropic scattering scenarios[C].2002 IEEE International Conference on Acoustics,Speech,and Signal Processing,2002:III-2833-III-2836.
[12] CHO Y,LEE J H.Effect of fading correlation on the SER performance of M-ary PSK with maximal ratio combining[J].IEEE Communications Letters,1999,3(7):199-201.
[13] LOYKA S L.Channel capacity of MIMO architecture using the exponential correlation matrix[J].Communications Letters,IEEE,2001,5(9):369-371.
[14] ZHOU Z,ISHIZAWA K,KIKUCHI H,et al.Generalized spatial correlation equations for antenna arrays in wireless diversity reception exact and approximate analyses[C].Proceedings of the 2003 International Conference on Neural Networks and Signal Processing,2003..IEEE,2003,1:180-184.
作者信息:
吴 鹏1,周 杰1,2,陈姜高路1,菊池久和2
(1.南京信息工程大学 电子与信息工程学院,江苏 南京210044;
2.日本国立新泻大学 工学部电气电子工学科,日本 新泻950-2181)

