0 引言

    DS证据理论因具有很强的处理不确定信息的能力，近年来在信息融合领域得到广泛应用。然而，如何构造DS证据理论中的基本概率赋值函数（Basic Probability Assignment，BPA），一直是信息融合中的一大难题。对此，许多学者都做出了研究^[1-8]。ZHU Y M等^[1]利用模糊-均值聚类实现了BPA的获取；蒋雯等^[2]基于样本差异度的方法构造初始BPA函数；FLOREA M C等^[3]基于隶属度生成BPA；周皓等^[4]将SVM通过Platt的概率模型来确定BPA；Ai Lingmei 等^[5]通过神经网络的输出来构造BPA。

    支持向量机（Support Vector Machine，SVM）是目前广泛应用的一种智能诊断分类器，该模型建立在统计学习理论和结构风险最小化原理上，不仅能够克服“维数灾难”、“过拟合”以及其他传统学习算法不可避免的问题，还在小样本学习问题上表现出较大优势。但SVM输出的是测试样本的类别标签，为硬输出，进行多个SVM输出映射时主要采用的是投票法，这很大程度上限制了SVM在信息融合领域中的应用。很多学者已经展开了对于SVM概率输出问题的研究^[9-12]。其中，由PLATT J C^[9]提出的计算后验概率的方法得到普遍的应用。

    本文提出一种SVM-DS决策融合方法，结合了DS与SVM的优点，同时解决了两者在实际应用中的一些局限性问题。通过Platt的概率模型分别将RBF核函数SVM分类器(SVM-RBF)、线性核函数SVM分类器(SVM-Linear)和多项式核函数SVM分类器(SVM-Quadratic)的硬输出转化为相应的后验概率；利用混淆矩阵来计算分类器的局部可信度；根据SVM后验概率以及分类器局部可信度，建立BPA函数，解决了DS理论在决策融合中BPA难以确定的问题。通过在UCI标准数据集、高速铁路转向架故障数据上的实验，也证明了本文决策融合方法能获得比单一分类器更高的分类准确率，且有效提高了方法稳定性。

1 DS证据理论

2 SVM介绍

2.1 SVM基本概念

2.2 SVM后验概率输出

    PLATT J C^[9]利用sigmoid函数，将SVM的硬输出映射到概率区间[0，1]，计算后验概率的模型为：

3 基于混淆矩阵的可信度计算

    在实际问题中，不同分类器对同一类别数据的识别能力是不一样的。将多个分类器的输出直接融合，没有考虑到分类器的可信度，这样可能会得到偏离实际的决策结果。因此，本文用混淆矩阵对分类器的局部可信度进行描述，并将得到的局部可信度作为DS融合时的折扣因子。

    假设待分类任务包含k个类别，数据集X中的样本数为M，每个模式类别中有Mi个样本(i=1，2，…，k)。利用分类器L对数据集分类后可以得到混淆矩阵C_l表示如下：

4 SVM与DS的融合分类方法

    (1)将训练样本分别通过SVM-RBF分类器、SVM- Linear分类器和SVM-Quadratic分类器进行训练，将各分类器的硬输出转化为软输出。

    (2)获得各分类器的混淆矩阵，计算出各分类器的局部可信度。

    (3)将获得的分类器局部可信度作为融合时的折扣因子。当分类器对某一样本x判决为w_i时，该分类器输出的结果可信度为PC(w_i)，后验概率为P_i，则按式(11)进行加权处理：

    (4)由式(11)获得DS决策融合时的BPA，通过DS融合得到最终决策结果。SVM-DS决策融合模型如图1所示。

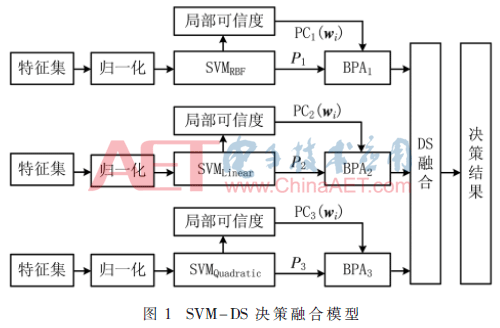
5 实验结果及分析

5.1 高铁转向架故障数据实验

    本文研究的高速列车转向架监测数据由实测得到。在速度为200 m/s的高速列车上共计安装了22个传感器，由此22个传感器对应输出的58个通道数据作为本文的实验数据。高速列车转向架单故障包含3种工况，分别为正常、横向减振器失效和抗蛇行减振器失效。

5.1.1 横向减振器单故障数据实验

    横向减振器失效包含4种不同故障类型，每种故障类型样本数均为140组。实验随机采用一半样本进行训练，另一半的样本用作测试。

    对高速列车横向减振器单故障的实测数据分别提取均值、方差、裕度指标等统计特征组成27维的特征集，特征分布情况见图2。

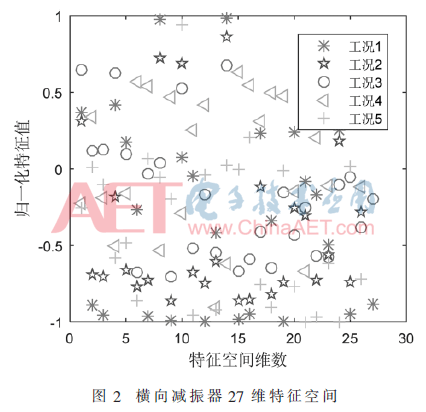
    将特征集输入不同核函数的SVM分类器得到混淆矩阵分别如下，其中CM¹、CM²、CM³分别表示SVM- Linear、SVM-Quadratic和SVM-RBF分类器输出的混淆矩阵。

    根据得到的混淆矩阵，由式（10）计算各分类器的局部可信度见表1。

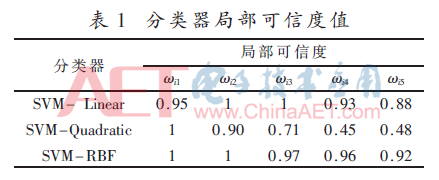
    按式（11）将局部可信度折扣到后验概率，再以DS理论融合后得到的分类混淆矩阵如下：

    对横向减振器单故障的测试样本最后的分类情况见表2。

    单一分类器中，SVM-Linear表现最好，SVM-Linear的标准差仅为0.008 6，稳定性明显高于其他两个单一分类器，其准确率为96.8%，略大于SVM-RBF分类器，比SVM-Quadratic高出2.09%。

    本文SVM-DS决策方法得到的准确率为97.41%，比单一分类器中表现最好的SVM-Linear分类器提高了0.61%。SVM-DS方法的标准差为0.005 5，稳定性远高于SVM-Quadratic和SVM-RBF分类器，比单一分类器中表现最好的SVM-Linear分类器的标准差降低了0.003 1，有效地提升了方法的稳定性。

5.1.2 抗蛇行减振器单故障数据实验

    抗蛇行减振器失效包含5种不同故障类型，样本数为150组。实验中随机采用一半的样本进行训练，另一半的样本用作测试。

    由于抗蛇行单故障中各故障类型之间相似度较大，因而各分类器得到的分类准确率都不太高。由表3知，在单一分类器中，SVM-RBF分类准确率为84.28%，高于其他两个分类器。SVM-Quadratic与SVM- Linear分类器分类准确率相差不大。就稳定性而已，表现最好的是SVM-Linear分类器。本文提出的SVM-DS决策融合方法准确率为86.14%，比单一分类器中表现最好的SVM-RBF提高了1.86%。SVM-DS方法标准差为0.016 1，比SVM-Linear降低了0.005 3，比SVM-Quadratic降低了0.011 5。可见在抗蛇行单故障中，SVM-DS决策融合方法的稳定性远高于各单一分类器。

    对比两种工况的分类结果可以看出，在横向减振器单故障实验中，表现最好的是SVM-Linear，在抗蛇行单故障实验中分类准确率最好的是SVM-RBF，稳定性最好的是SVM-Linear。这说明，分类器对不同故障数据的分类能力是不一样的，单一分类器几乎无法做到对各种工况的故障数据都表现良好，这也是本文要采用多分类器联合的决策融合方法的原因。高铁转向架单故障数据实验验证了本文SVM-DS决策融合方法的有效性，该方法实现了故障分类的优化，稳定地提升了故障识别率。

5.2 UCI标准数据集验证

    为了充分验证SVM-DS决策融合方法的有效性，本文使用表4所示UCI数据集进行实验分析。

    限于篇幅，特征分布图以Iris数据集的特征集为例。图3是Iris标准数据集是特征集归一化后的特征分布图。

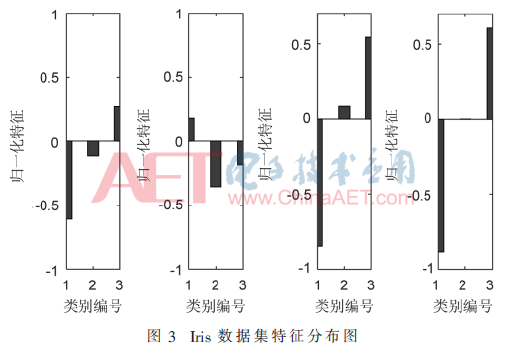
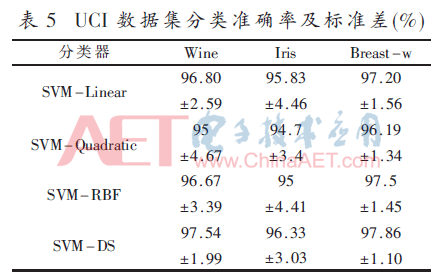
    在Wine和Iris数据集上，单一分类器表现最好的都是SVM-Linear分类器。在Breast-w数据集上，不同核函数SVM分类器分类效果差异不大。但SVM-DS方法在3种数据集上的准确率都高于各单一分类器，稳定性也是最好的。这验证了SVM-DS方法在UCI标准数据集上提高分类准确率的同时，也提高了方法的稳定性。

6 结束语

    本文提出一种基于SVM与DS相结合的决策融合方法。该方法根据SVM的实际分类结果，从中获取分类标签、后验概率和混淆矩阵等信息。用混淆矩阵来衡量分类器性能，计算局部可信度，再结合SVM分类器后验概率来构造BPA，使获得的基本概率赋值函数更加可靠和符合实际，从而有效解决了证据理论应用中的一大难题。从实验结果可以看出，与单一分类器的分类结果相比，结合3种不同SVM分类器的SVM-DS决策融合方法能够稳定地提高分类准确率。 

参考文献

[1] ZHU Y M，BENTABET L，DUPUIS O，et al.Automatic determination of mass functions in Dempster-Shafer theory using fuzzy c-means and spatial neighborhood information for image segmentation[J].Optical Engineering，2002，41(4)：760-770.

[2] 蒋雯，陈运东，汤潮，等.基于样本差异度的基本概率指派生成方法[J].控制与决策，2015，30(1)：71-75.

[3] FLOREA M C，JOUSSELME A L，GRENIER D，et al.Approximation techniques for the transformation of fuzzy sets into random sets[J].Fuzzy Sets and Systems，2008，159(3)：270-288.

[4] 周皓，李少洪.支持向量机与证据理论在信息融合中的结合[J].传感器技术学报，2008，21(9)：1566-1570.

[5] Ai Lingmei，Wang Jue，Wang Xuelian.Multi-features fusion diagnosis of tremor based on artificial neural network and D-S evidence theory[J].Signal Processing，2008，88(12)：2927-2935.

[6] Han Deqiang，Deng Yong，Han Chongzhao.Novel approaches for the transformation of fuzzy membership function into basic probability assignment based on uncertain optimization[J].International Journal of Uncertainty Fuzziness and Knowledge-Based Systems，2013，21(2)：289-322.

[7] 韩德强，杨艺，韩崇昭.DS证据理论研究进展及相关问题探讨[J].控制与决策，2014，29(1)：1-11.

[8] SUH D，YOOK J.A method to determine basic probability assignment in context awareness of a moving object[J].International Journal of Distributed Sensor Networks，2013(2)：167-174.

[9] PLATT J C.Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods[J].Advances in Large Margain Classifiers，2000，10(4)：61-74.

[10] 王磊.支持向量机学习算法的若干问题研究[D].长沙：国防科学技术大学研究生院，2009.

[11] CHANG C C，LIN C J. LIBSVM：a library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology(TIST)，2011，2(3)：1-27.

[12] 雷蕾，王晓丹，邢雅琼，等.结合SVM和DS证据理论的多极化HRRP分类研究[J].控制与决策，2013(6)：861-866.

[13] 张静，宋锐，郁文贤，等.基于混淆矩阵和Fisher准则构造层次化分类器[J].软件学报，2005，16(9)：1560-1567.

[14] 袁宪锋，宋沐民，周风余，等.多PCA模型及SVM-DS融合决策的服务机器人故障诊断[J].振动、测试与诊断，2015，35(3)：434-440.

作者信息:

朱  菲，金炜东

（西南交通大学 电气工程学院，四川 成都610031）