0 引言

    采样作为数字处理的前提和基础，一直以来都是信号处理领域的热点。但是随着各领域信号带宽不断增加，信号频率不断增大，目前的商用数字模拟转换设备（Analog-to-Digital Convertor，ADC）已经难以达到所需的采样率要求，就算达到了采样率要求，大量的样本数据的存储和传输也将是一大难题。压缩感知(Compressed Sensing，CS)^[1-2]的出现解决了稀疏宽带信号采样后数据量过大的问题，ELDAR Y^[3-4]团队基于此理论提出了调制宽带转换器(Modulated Wideband Converter，MWC)系统及其硬件实现方案，实现了稀疏多带信号的同步压缩采样。由于通信、雷达、医疗等应用领域的信号都可以建模为稀疏多带信号，因此MWC结构具有很强的实用性。MWC由天线作为信号接收装置，接收到的无线传输信号为低功率信号，信号不可避免会混入噪声，现有的重构算法都对噪声比较敏感^[5-11]，这将直接影响恢复效果。因此有必要将经过MWC系统得到的样本数据进行预处理，去除噪声后再进行重构。

    本文将小波阈值去噪的思想引入到MWC系统中，为了尽可能保留信号的边缘信息，提出了基于小波区域阈值去噪的优化还原算法。首先对样本进行平稳小波变换（Stationary Wavelet Transform，SWT），根据设计的小波系数的选取规则选择将小波系数置零或保留；然后通过小波重构恢复信号,得到去噪过后的样本数据，将去噪过后的样本信号与去噪前的样本信号相加作为新的样本，利用现有恢复算法求解支撑集，将该支撑集与不去噪直接求解的支撑集求并集得到最终的支撑集，最后通过求伪逆得到原始信号的恢复信号。

1 MWC的研究现状

    MWC^[3]的系统框图如图1所示，稀疏多带信号x(t)同时进入m个通道，与在各通道内的周期为T_p的在±1之间随机变化的伪随机序列p_i(t)进行混频。混频后通过截止频率为f_s/2的低通滤波器进行滤波，其中f_s=1/T_s。最后通过采样率为f_s的ADC得到m组采样序列y_i(n)。将采样序列y_i(n)送入恢复算法进行恢复，即可求得原始稀疏多带信号x(t)的支撑集，进而通过频谱逆搬移重建出信号。

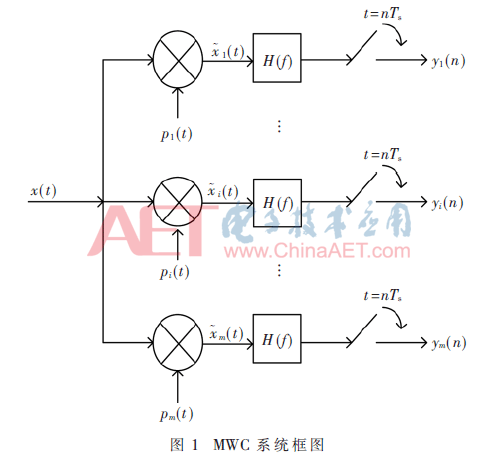
    支撑集重构作为MWC系统的核心部分之一，一直以来都广受关注^[5-11]。近年来提出的多种算法中正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法^[5]是最经典的恢复算法。ReMBo^[6]、RPMB^[7]、RMMV^[8]、MVT等算法都在一定程度上提高了恢复速率，ISOMP算法^[10]提高了在高信噪比（Signal to Noise Ratio，SNR）条件下的信号重构概率。由上可知，目前的MWC恢复算法研究大多集中于提高恢复速率及改进高SNR条件下的恢复率，在对低信噪比下的恢复性能的改善方面没有太多进展。

2 基于小波区域阈值去噪的MWC优化还原算法

    传统的信号去噪方法主要有：傅里叶变换、Wiener滤波、中值滤波、均值滤波、经验模态分解（Empirical Mode Decomposition，EMD）、小波变换等。傅里叶变换去噪适用于信号与噪声不重合或重合较少的情况，在MWC系统中，采样之前已经有一个低通滤波器滤除了不需要的高频部分，剩下的低频部分中信号与噪声是重叠的。Wiener滤波适用于信号的基准信号已知的情况，而MWC系统中，样本信号来源于输入信号x(t)与伪随机序列p_i(t)的混频，是完全随机的，无法提供该基准信号。中值滤波与均值滤波都对噪声进行平滑，对冲击变化的保留效果不好。EMD分解^[12]速度非常慢，严重影响了MWC的恢复速率。而小波变换由于其多分辨率特性，能够有效检测到信号的突变点，进而区分信号的突变部分和噪声，从而广泛地应用于信号和图像的去噪^[13-14]。

    小波变换与傅里叶变换不同，傅里叶变换在频域有较好的局部化能力，但是在时域没有局部化能力，在频域的微小变化都会使时域每个位置的值产生变化。而小波变换在时频域都是局部的，能很好地对各时刻附近的频率信息进行处理。因为MWC中输入信号x(t)是实时连续信号，伪随机序列p_i(t)是随机的序列，所以样本信号是完全随机的，在任一时刻附近的频率特征都很重要。所以用小波变换分析MWC样本将大大提高准确率。且快速傅里叶变换的时间复杂度是O(nlog₂(n))，而快速小波变换的时间复杂度是O(n)，所以一般情况下，快速小波变换比傅里叶变换快。用下面的公式定义f(n)，n=1，…，N的小波分解：

2.1 小波阈值去噪原理

    DONOHO D^[15]提出小波阈值去噪以来，很多人在其上做了改进。主要思想为：对含噪信号进行各尺度下的小波分解，保留大尺度下的全部小波系数，对于各小尺度下的小波系数设定一个阈值，幅值低于该阈值的小波系数置为0，高于该阈值的小波系数完整保留或做相应收缩处理，最后将处理过后的小波系数利用小波逆变换进行重构，得到去噪后的信号。

    对小波系数一般采用软阈值和硬阈值方法进行处理^[16]。软硬阈值各有优缺点，软阈值整体连续性好，但是软阈值函数对大于阈值的小波系数进行恒定压缩，直接影响了重构信号与真实信号的逼近程度，而硬阈值则相反，本文采用如式(2)所示的阈值折中方法，利用一个调节因子α对阈值进行调节，在SNR较低时可将其设置得大一点，SNR较高时可设置得小一点，一定程度上避免了过平滑带来的失真。

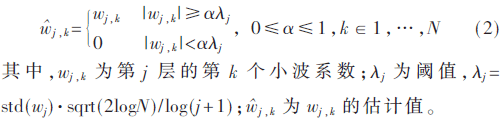
2.2 小波区域阈值去噪

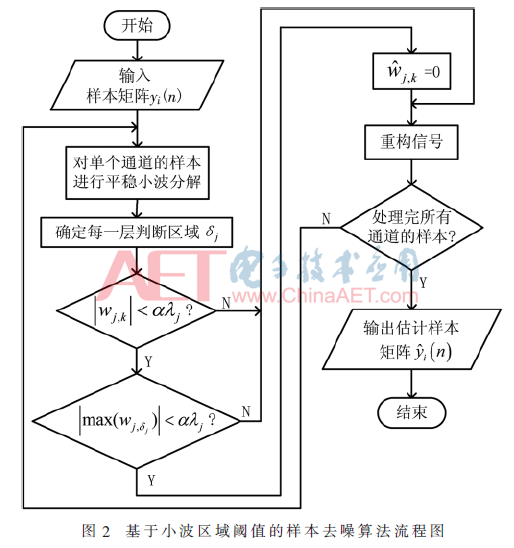
    以上的小波阈值去噪在去除噪声的同时将幅度较小的信号也去除了，直接影响重构信号的准确度。考虑到噪声幅度是随机的，但是信号幅度是连续变化的，所以本文提出了基于小波区域阈值去噪的MWC优化还原算法，首先对样本进行小波区域阈值去噪，然后将MWC样本去噪后与原样本相加得到新的样本，达到增强信号的目的，再用现有恢复算法求解支撑集，将该支撑集与不去噪直接求解的支撑集求并集得到最终的支撑集，最后通过求伪逆得到原始信号的恢复信号。该去噪方法能在有效平滑噪声的同时保留信号的边缘特性，如式（3）所示：

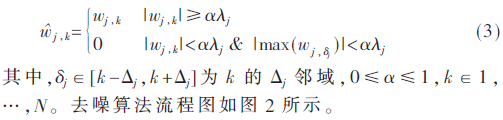
3 实验仿真与结果分析

    为了验证本算法的有效性，本节设计了3个实验：

    (1)随机取一个单通道的样本，进行小波区域阈值去噪，对比去噪前后的样本信号。

    (2)利用OMPMMV算法求解支撑集。相同条件下对比原始信号、去噪前的恢复信号、去噪后的恢复信号。

    (3)相同条件下对比去噪前与去噪后的恢复成功率。

    采用文献[3]中的信号模型和采样参数，实验中的多带信号由式(4)产生：

其中，参数E_i、B_i、f_i、τ_i分别代表第i个频带的能量系数、带宽、载波频率和延迟时间；n(t)为高斯白噪声；N为频带数。以下实验以6个(对称的3对)频带的信号为例，具体信号参数设置为：E={1，2，3}；B={50，50，50}MHz；τ={6.989，3.994，2.995}μs；载波频率随机分布在[-f_nyq/2，f_nyq/2]，f_nyq=10 GHz；伪随机序列长度L=195；f_s=f_p=f_nyq/L=51.28 MHz。

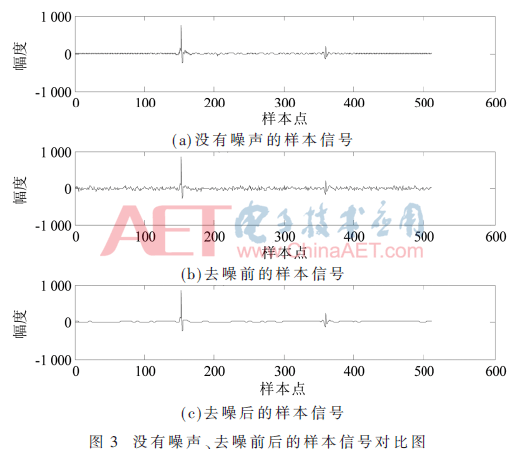
    设置SNR=0 dB，通道数m=50，每通道样本长度为512。随机取一个通道的样本进行小波区域阈值去噪，其中小波基为db1，分解层数为5，对前4层采取区域阈值去噪，第5层小波系数不变，前4层的判断区域分别设置为[k-3，k+3]、[k-4，k+4]、[k-5，k+5]、[k-10，k+10]，阈值调节因子α=0.5。图3为无噪声样本、有噪声样本以及对有噪声样本去噪后的样本信号对比图，可以看出本文的方法可以有效去除部分噪声。

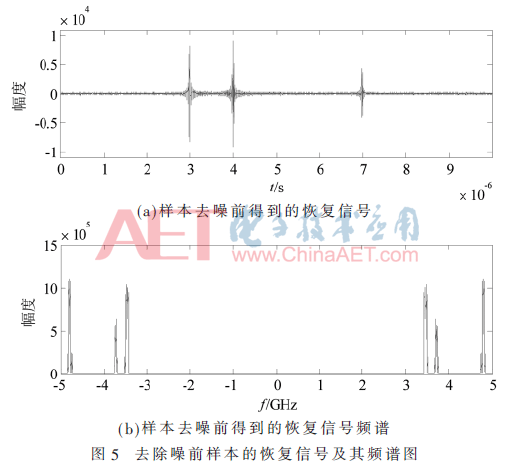
    在以上实验的基础上设置SNR=10 dB，图4为一个加入高斯白噪声的信号及其频谱图。图5和图6分别显示出图4信号MWC采样后用去噪前的样本和去噪后的样本恢复的信号及其频谱图。从图5和图6可以看出，此时，去噪后样本的恢复效果在时域和频域显示都很好。

    计算恢复成功率时，进行500次蒙特卡罗实验，将支撑集恢复成功的百分率作为恢复率。这里的恢复成功计算方法见文献[3]。图7给出了在以上实验的基础上，当SNR∈[-10,20]dB时去噪前后的重构成功率对比图。可见去噪后的方法在SNR较小时相对于去噪前恢复效果更好，重构率最高可以比去噪前高21.8%(SNR=-6 dB时，去噪前后恢复率分别为43%、64.8%)。

4 结论

    本文利用小波阈值去噪思想，提出了基于小波区域阈值去噪的MWC优化还原算法，在去除样本噪声的同时尽可能保留了信号的边缘信息。仿真实验表明，本文的算法恢复性能优于去噪前，且在SNR较低时，效果更明显，重构率最高可以比去噪前高21.8%。本文的算法因为是直接对样本进行操作，所以可移植性强，可以与其他的减少通道数、减少运行时间等算法并用，进一步提高整个系统的性能。

参考文献

[1] CANDES J，ROMBERG J，TAO T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory，2006，52(2)：489-509.

[2] DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory，2006，52(4)：1289-1306.

[3] MISHALI M，ELDAR Y.From theory to practice：sub-nyquist sampling of sparse wideband analog signals[J].IEEE Journal of Selected Topics in Signal Processing，2010，4(2)：375-391.

[4] MISHALI M，ELDAR Y，DOUNAEVSKY O，et al.Xampling：analog to digital at sub-nyquist rates[J].IET Circuits Devices & Systems，2011，5(1)：8-20.

[5] Chen Jie，Huo Xiaoming.Theoretical results on sparse representations of multiple-measurement vectors[J].IEEE Transactions on Signal Processing，2006，54(12)：4634-4643.

[6] MISHALI M，ELDAR Y.Reduce and boost：recovering arbitrary sets of jointly sparse vectors[J].IEEE Transactions on Signal Processing，2008，56(10)：4692-4702.

[7] 盖建新，付平，孙继禹，等.基于随机投影思想的MWC亚奈奎斯特采样重构算法[J].电子学报，2014，42(9)：1686-1692.

[8] Yao Bo，Li Zhi，Hua Wei，et al.Efficient recovery of support set in modulated wideband converter system[J].Journal of Information and Computational Science，2015，12(16)：6043-6055.

[9] 邓伯华，李健，李智.基于测量向量转换的MWC支撑集恢复算法[J].四川大学学报(工程科学版)，2015，47(2)：161-165.

[10] Jia Min，Shi Yao，Gu Xuemai，et al.Improved algorithm based on modulated wideband converter for multiband signal reconstruction[J].EURASIP Journal on Wireless Communication and Networking，2016，2016(1)：1-9.

[11] 那美丽，周志刚，李霈霈.基于稀疏傅里叶变换的低采样率宽带频谱感知[J].电子技术应用，2015，41(11)：85-88.

[12] 徐晓刚，徐冠雷，王孝通，等.经验模式分解(EMD)及其应用[J].电子学报，2009，37(3)：581-585.

[13] HASSANEIN M，HANNA M，SEIF N，et al.Signal denoising using optimized trimmed thresholding[J].Circuits Systems & Signal Processing，2018，37(6)：2413-2432.

[14] 刘明君，董增寿.基于改进小波变换的手臂肌电信号去噪算法的研究[J].电子技术应用，2018，44(3)：122-125.

[15] DONOHO D.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory，2002，41(3)：613-627.

[16] 赵瑞珍，宋国乡，王红.小波系数阈值估计的改进模型[J].西北工业大学学报，2001，19(4)：625-628.

作者信息:

文婉滢，李  智

（四川大学 电子信息学院，四川 成都610065）