0 引言

    实际运动中的载体动力学模型误差不可避免，而观测噪声的统计特性又具有不确定性，无法完全模型化，观测粗差对导航精度的影响也不容忽略^[1-3]。结合上述因素，组合滤波模型的精确度无法得到保障，卡尔曼滤波在组合导航中的应用也会失去最优性，使状态估计值精度降低，甚至发散^[4]。因此需要在最初卡尔曼滤波（标准卡尔曼滤波或非线性卡尔曼滤波）的基础上增加抗差性与自适应性，补偿上述因素对组合导航的影响，提高组合导航性能^[5-6]。本文提出一种RAEKF方法。基于惯性导航、卫星导航原理与误差模型确定紧组合工作模式下的卡尔曼滤波数学模型推导常用EKF模型并构造抗差自适应卡尔曼滤波，通过自适应调整观测值的使用权重提高滤波精度。

1 GPS/INS紧组合误差观测方程建立

1.1 状态方程

    基于伪距/伪距率紧组合模式，GNSS状态方程与INS状态方程构成组合导航卡尔曼滤波器状态模型。利用状态扩充法将GNSS误差状态作为状态变量扩充到组合系统整体状态量中，GNSS的误差状态取接收机钟差与钟频。在实际应用中通常取等效时钟误差相应的距离率δt_u与等效时钟频率误差相应的距离率δt_ru，其相关时间为：

1.2 伪距观测方程

    由INS解算得到的载体所在三维的位置信息(x_I，y_I，z_I)，根据卫星星历解算可见卫星在地心地固坐标系下的三维位置信息为(x_S，y_S，z_S)，则可以计算得到在INS中载体到第i颗卫星的伪距为：

其中，v_ρi为多路径效应、对流层延迟误差、电离层误差等引起伪距观测噪声。因为δ_tu是伪距观测中的主要误差源，因此在建立伪距模型时，也应要考虑上述因素对伪距观测值造成的影响。则伪距测值可以写成：

1.3 伪距率观测方程

    基于INS推算载体与卫星i之间伪距率为：

2 抗差自适应原理分析

    利用抗差估计原理能够抵制观测粗差对滤波结果的影响，另外抗差自适应因子使滤波参数自适应调整，从而达到参数的最佳值。由上一节状态方程和观测方程可知其状态估计协方差为：

3 紧组合EKF滤波建模

    EKF是在最小方差准则下针对非线性系统的次优滤波器，易于实现，是常用非线性滤波。它通过对非线性系统进行一阶泰勒线性展开，高阶项截断，再应用卡尔曼滤波模型递推解算的非线性算法。

    同理，观测矩阵为：

    EKF滤波应用必须满足两点假设：(1)满足小扰动假设，即非线性方程的理论理与实际解之差为小量，即EKF只适合弱非线性系统，但在强非线性系统中，这些假设条件很可能会破坏滤波器的性能，导致滤波结果不准确甚至发散；(2)需要计算Jacobian矩阵及其幂。

4 实验结果及分析

    车载实验过程中易受周围建筑物遮挡或干扰，使导航结果受观测卫星条件观测限制。可见卫星数目少于4颗时或者卫星几何结构PDOP不佳，导致在预测残差中无法分辨出上述误差带来的影响。尤其在紧组合过程中，观测量是卫星原始观测信息，若不预处理，观测值质量很难得到保证。通过对自适应因子作适当改进以适应紧组合工作原理与实际需求：

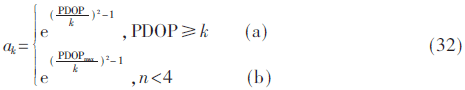
式中，k为PDOP值的阈值；n为可见卫星个数。当PDOP<k、n>4时，即可见卫星几何分布较合理，卫星观测条件好，无需自适应过程，只进行标准EKF滤波；当PDOP≥k、n>4时，即可见卫星几何分布不佳，利用式(32)中式(a)自适应因子抑制对导航误差的影响；当n<4时，可见卫星数目较少，也无法进行PDOP计算，利用式(32)中式(b)构造自适应因子，使组合导航系统性能主要依赖惯性导航解算结果。实验中设定阈值k=7，其滤波结果如图1和图2所示，导航误差特性统计如表1所示。

    根据卫星可见数目与卫星几何结构PDOP构造抗差自适应因子，当可见卫星数目不足或几何分布不佳的状态下，尤其本次实验中604～606 s、1 108 s～1 110 s及1 130～1 133 s这三个时间段，降低对卫星观测数据的权重，避免观测值不佳状态对滤波结果的影响，使组合导航性能更依赖于惯性导航解算结果。从图1和图2可看出在三个时间段内速度误差、位置误差得到了有效抑制。表1中也进一步验证了数据统计特性值得到一定改善。

5 结论

    本文针对模型不准确与解决卫星观测粗差问题研究了抗差自适应算法，围绕载体运动难免会受到外界因素的干扰且观测粗差不可避免，构造基于预测残差向量构造的抗差自适应滤波。实验结果表明，基于RAEKF的紧组合方案获取的水平位置误差优于3 m、高度误差优于8 m、三个方向上的速度误差优于0.24 m/s，该结果可满足车载导航需求，为进一步提升系统动态定位精度提供技术支撑。

参考文献

[1] LI Z，WANG J，LI B，et al.GPS/INS/O dometer integrated system using fuzzy neural network for land vehicle navigation applications[J].Journal of Navigation，2014，67(6)：967-983.

[2] 孙伟，段顺利，孔莹，等.基于GPS广播星历的载体速度和加速度多普勒测定方法[J].传感技术学报，2017，30(11)：1630-1635.

[3] 谭兴龙，王坚，赵长胜.神经网络辅助的GPS/INS组合导航自适应UKF算法[J].测绘学报，2015，44(4)：384-391.

[4] YANG Y X，HE H，XU G.Adaptively robust filtering for kinematic geodetic positioning[J].Journal of Geodesy，2001，75(2)：109-116.

[5] 杨元喜，任夏，许艳.自适应抗差滤波理论及应用的主要进展[J].导航定位学报，2013，1(1)：9-15.

[6] YANG Y X，SONG L，XU T.Robust estimator for correlated observations based on bifactor equivalent weights[J].Journal of Geodesy，2002，76(6)：353-358.

作者信息:

李敏涛

(温州职业技术学院 电气电子工程系，浙江 温州325000)