0 引言

    功率因数校正（Power Factor Correction，PFC）引起国内外许多研究者的关注，与传统的三相PFC拓扑相比，VIENNA整流器拓扑结构具有开关器件较少、开关应力小、无死时间、效率高等优点^[1]。新型VIENNA整流器中的LCL滤波器，它可以有效降低输入电流谐波，在单位功率下高效运行。该拓扑应用在非车载充电机前级等领域有着重要的地位。

    文献[2]采用改进的准直接功率控制的双环结构抑制LCL滤波的谐振峰值，整流器的性能得到提升。文献[3]运用DSP控制芯片内部的数字延时设置谐振频率；前馈占空比控制，对PFC的LCL滤波中出现过渡补偿进行修正。文献[4]从工程设计的角度优化控制环路中指定次谐波，减小输入电流畸变。

    传统的参数整定方法存在整定耗时、设计复杂等缺点。随着人工智能技术的蓬勃发展，文献[5]～[7]运用智能算法对逆变器或整流器的控制器参数进行优化，校正结果显著，其中粒子群优化性能独特。

    本文通过VIENNA整流器的建模，设计LCL滤波器和PI控制器，提出了一种多目标多群体多位置多速度粒子群优化(MMMMPSO)算法，对其参数整体优化。建立离线优化模型，仿真对比标准粒子群(PSO)下的VIENNA整流器的优化效果。搭建一台5 kW三相整流器实验样机，证明该方案的可靠性和正确性。

1 三相VIENNA整流器的设计

1.1 LCL滤波器的数学模型及设计

    LCL滤波器的VIENNA整流器拓扑如图1所示^[1]。LCL滤波器可改善传统L滤波器的缺点，但参数设计复杂且工作量较大。简化LCL滤波模型及设计如下。

    将a相电路建立其数学模型为：

1.2 PI数字控制器的设计

    为降低模型的复杂度，按传统L滤波器的拓扑结构，即L=L_g+L_r。VIENNA整流器在abc轴系下各相间较强的耦合性不利于控制器设计。内环电流经过坐标变换后，dq轴间的耦合影响较小，可看成具有对称性的控制，只需单独考虑一个轴。以d轴为例，d轴控制有外环直流电压控制，q轴则没有，其指令电流为给定值，PI控制的三相整流系统结构框图如图2所示。

    图中u_dref、e_d(s)、e_dn(s)、i_dref、R_L(s)、i_d、i_do、u_dc分别为直流电压指令信号、外环指令电压信号与反馈电压信号的误差、内环指令电流信号与反馈电流信号的误差、交流侧输出信号、直流侧负载、电流指令信号、直流侧负载电流、直流侧负载电压。K_Pv、K_Iv分别为电压环比例、积分系数；K_Pi、K_Ii分别为电流环比例、积分系数；T_s、K_pwm分别为采样周期和PWM模块等效增益。

2 MMMMPSO和离线优化模型

2.1 MMMMPSO的原理和设计

    本文提出一种新颖MMMMPSO算法。多目标优化克服了传统单目标的局限性获得最优解。主种群和若干辅助种群构成整个种群。每个辅助种群剔选单个目标类中的粒子独立优化，保证了种群的多样性；由信息交叉选择演变给主种群优化整体目标，保证算法的收敛性。多位置多速度能够更好权衡局部和全局最优，进一步提高迭代范围。此算法的整体构架如图3所示。

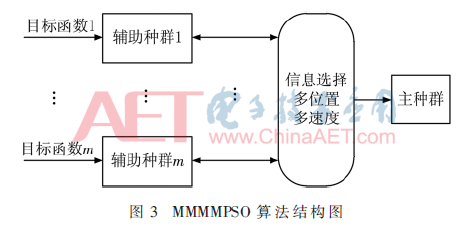
2.1.1 主种群与多位置更新方式

    主种群更新方程基于标准粒子群^[8]，定义如下：

其中w_max、w_min、t、t_max、k和r₃分别为最大惯性权重、最小惯性权重、当前迭代、最大迭代、常数和随机区间[0，1]。

2.1.2 辅助种群与多速度更新方式

    辅助种群使粒子群中较差的粒子通过多次迭代信息选择获得最小适应值，形成新的种群增强主种群的多样性。多速度由改进的压缩因子更新法及混沌更新法组成。

    (1)利用压缩因子改进的速度更新如下式：

式中τ为经验值。

    混沌变量为：

2.2 优化目标函数

2.2.1 LCL滤波器的参数优化

    粒子群优化的个体粒子由一组4维向量表示为：X=[L_g L_r C_f F]，其最后一项为粒子的适应值。目标函数为式(2)、式(3)；约束条件为式(4)~式(8)。

2.2.2 PI数字控制器的参数优化

    三相旋转坐标系下的控制为直流量，为保证e_d(s)、e_dn(s)的值及id的总谐波畸变率都尽可能小，将总谐波畸变率（THD）和时间乘以误差绝对值积分（ITAE）作为三相PI控制的整流系统优化目标函数。该组合公式为：

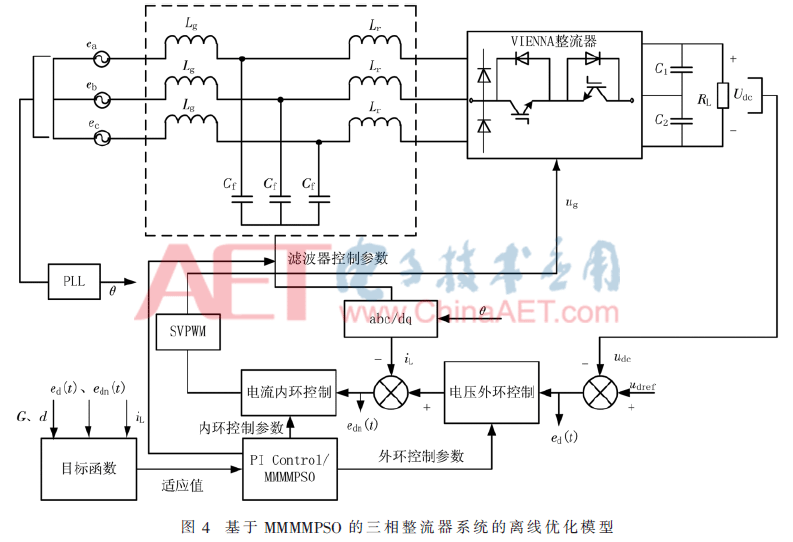
2.3 系统的离线优化模型

    基于MMMMPSO的三相整流系统离线优化模型如图4所示。

3 仿真与实验

3.1 仿真结果分析

根据上述分析建立MATLAB/Simulink仿真模型，主要参数为输入三相相电压220 V，额定输出电压560 V，直流侧电容(c1=c2)0.6 mF，开关频率100 kHz。基于PSO与MMMMPSO的系统在稳态下的电网侧电压电流均高度近似正弦波且同相位，但后者纹波较小，明显改善了波形。然后分别对输入电流快速傅里叶分析(FFT)如图5所示。PSO的THD为20.65%，MMMMPSO的THD为1.88%。表明MMMMPSO能有效避免粒子群陷入局部最优区域而无法跳出的情况出现，有高效的抑制谐波能力。

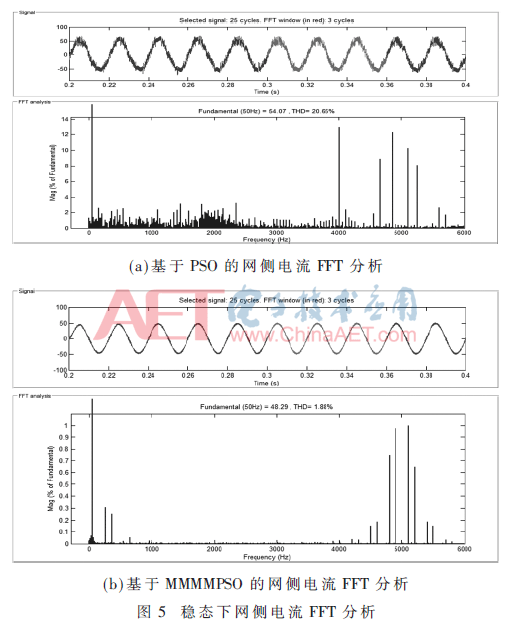
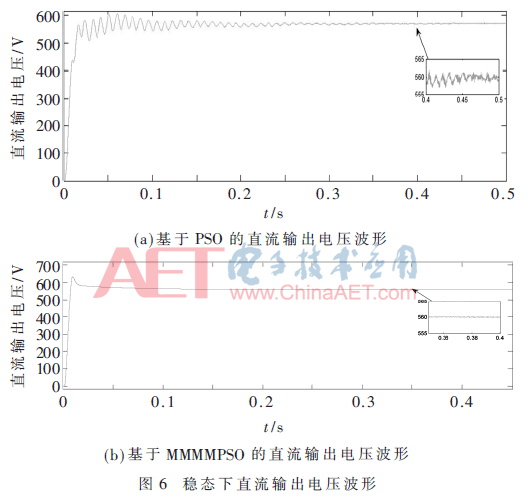
    图6是两者的直流输出电压波形。图6(a)为输出电压在0.35 s左右时趋于稳定，响应和超调都较为理想。图6(b)为输出电压在0.17 s左右达到平衡且稳态性更好。

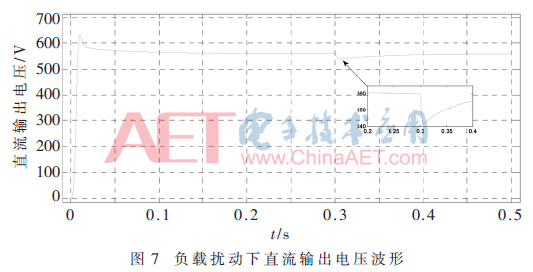
    在0.03 s时MMMMPSO系统下切载动态响应如图7所示。直流输出电压跃变后迅速恢复于给定值560 V。负载扰动下网侧电压电流波形如图8所示，可知网侧电流突增1倍而网侧电压不变，仍然接近同相脉动。

3.2 实验验证

    本文采用DSP控制芯片TMS320F28033，基于MMMMPSO优化算法，搭建一个5 kW三相VIENNA整流器实验样机平台，样机参数和仿真参数相同。

    稳态时a相网侧电压电流及输出电压波形如图9所示；负载突变从2.5 kW到5 kW时网侧电压电流和输出电压波形如图10所示。同步状态下整流器功率因数基本是1且谐波含量满足设计要求；网侧电流始终呈正弦化且过渡平稳；输出电压纹波较小且动态响应良好。

4 结论

    本文设计一种基于新颖粒子群算法应用在三相VIENNA整流器中。主要利用MMMMPSO算法对整流器的前端LCL滤波器和PI数字控制器参数的优化，通过与传统PSO的仿真对比表明，改进的算法有效改善了网侧电流波形且降低了其总谐波畸变率，整流器输出电压获得了良好的稳态与动态性能。由实验样机验证，当负载突变时，输入电流和输出电压都在极短时间获得动态平衡，输入电压电流始终保持同步，表明VIENNA整流器在该方案下有较强的鲁棒性和优越性。

参考文献

[1] VIITANCE T，TUUSA H.Space vector modulation and control of a unidirectional three phase/switch VIENNA I rectifier with LCL-type AC filer[C].Power Electronics Specialist Conference，2003.PESC’03.2003 IEEE 34th Annual，2003(3)：1063-1068.

[2] 王晓刚，谢运祥，张杰，等.LCL滤波PWM整流器的新型准直接功率控制[J].电力系统保护与控制，2013，41(9)：80-85.

[3] 林壮.VIENNA拓扑整流器的控制技术研究[D].杭州：浙江大学，2014.

[4] 刘源，梅烨，曹丰文，等.VIENNA整流器的设计与优化[J].电源学报，2018(2)：110-118.

[5] 赵葵银.PWM整流器的模糊滑模变结构控制[J].电工技术学报，2006，21(7)：49-53.

[6] Sun Wei，Chen Zhe，Wu Xiaojie.Intelligent optimize design of LCL filter for three phase voltage source PWM rectifier[C].2009 IEEE 6th International Power Electronics and Motion Control Conference，2009：970-974.

[7] Ren Haipeng，Guo Xin.Optimization controller design of CACZVS three phase PFC converter using particle swarm optimization[C].IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society，2014：1665-1671.

[8] SHI Y，EBERHART R.A modified particle swarm optimizer[C].IEEE International Conference on Evolutionary，1998：69-73.

作者信息:

许文钱，邵如平，袁东林

(南京工业大学 电气工程与控制科学学院，江苏 南京211816)