0 引言

    忆阻器是由物理学家蔡少棠教授在1971年提出的第四种电路基本元器件，其忆阻值联系磁通量和电荷量两个电路参量^[1]。由于其非易失性（忆阻值可以存储起来）、忆阻值可通过对器件端压的调制实现连续变化等优点，可作为神经元突触来构建神经网络^[2]。

    研究发现同一个忆阻器在相同的驱动下测得的多条传输特性曲线之间存在差异；相同制造工艺下，不同忆阻器的性能也不一样，即忆阻器件的性能并不稳定^[3]。这些稳定性问题会对忆阻神经网络的收敛速度和功能实现产生影响。

    本文的研究目的是基于一种具有等效电阻拓扑结构的忆阻器模型，探究忆阻器稳定性问题对忆阻神经网络性能的影响，从而得出在保证忆阻神经网络性能的前提下模型参数的允许波动范围。根据忆阻器模型参数的意义，映射到器件工艺层次的参量波动，为忆阻器件的工艺制造和选型提供参考。

1 忆阻器模型及稳定性仿真

    本文采用了一种具有等效电阻拓扑结构的忆阻器模型，该模型不仅能描述忆阻器的传输特性，而且能准确描述忆阻器的不稳定现象。通过设置波动的忆阻器参数，模拟忆阻器的不稳定性，为忆阻神经网络的搭建做准备。

1.1 忆阻器模型

    随着忆阻器研究的发展，很多证据表明忆阻器的电阻转换现象是由于器件中作为导电通道的导电丝的形成和消失造成的^[4]，外加电压控制着导电丝的形成和消失，这样就可以把忆阻器划分为通道区域和无通道区域，导电通道则包括高阻和低阻区域，然后再通过一个合适的拓扑结构将这若干个通道结合起来，这就是本文使用的忆阻器模型^[5]。其示意图及数学模型简化过程如图1所示。图(a)为忆阻器件结构图，可等效为图(b)，其中由斜划线填充的柱体表示无通道区域，阻值远大于有通道区域(其他柱体)，故由于并联可进一步简化为图(c)。

    基于上述模型的数学表达式如下，假设在忆阻器中存在N个导电通道，即图1(c)中的通道数，R_l表示低阻区域完全占据通道时一个导电通道的阻值；R_h表示高阻区域完全占据通道时一个导电通道的阻值。D为导电通道的总长度，X_i为低阻区域占据通道的长度(X_i≤D)。

    所以，第i个导电通道的忆阻值为：

其中，C_i指定一个统计分布来描述在忆阻器中导电通道长度的不均匀性，θ和α决定通道的初始状态，θ用来调制C_i以给出合适的初值，α则对其进行进一步的调控；γ₀用来对通道初始长度进行微调；β和λ则描述随着磁通量(偏压v(t)对时间t的积分)的积累，导电通道的动态变化过程。

    将式(5)、式(6)、式(7)带入式(4)得忆阻值M：

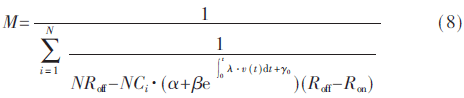
1.2 忆阻器稳定性仿真

    将上述模型应用于一个Pt/TiO₂/TiO_2+x/Pt结构的实际忆阻器件中，对各项参数设值为：D=20 nm，R_off=1.39 kΩ，R_on=25 Ω，N=20。θ=0.05和α=1决定初始导电通道长度及其分布，γ₀=-5.9对初始长度进行微调。λ=5.76和β=1将状态转换速度限制在一个比较低的水平，这种情况下忆阻值只能在25 Ω~220.71 Ω的范围内变化，通过MATLAB仿真得到该模型在周期性电压下I-V特性曲线，即如图2中所示β=1对应的曲线。

    该伏安特性曲线的形状表现为滞回曲线，而且忆阻值随时间变化的趋势与忆阻器相同，在后文中，以该忆阻器模型各参数的取值变化来模拟忆阻器的不稳定性。图2为参数β不同取值时忆阻器的传输特性曲线，其他参数α、γ₀、λ不同取值时与之类似。这种对忆阻器不稳定性的模拟结果与YANG J J等人搭建的忆阻器测试得到的不稳定性表现类似^[6]，说明该模型可以作为忆阻器件的仿真模型。

2 忆阻BP神经网络设计与实现

    为了探究忆阻器的稳定性对忆阻神经网络的收敛速度和准确性的影响，搭建了一个三层的忆阻BP神经网络，并用手写数据集MNIST进行训练和测试。

2.1 忆阻BP神经网络MATLAB实现

    本文中使用MNIST数据集^[7]搭建3层全连接忆阻BP神经网络，网络结构为：输入层785个节点(图片28×28个输入节点和一个偏置点)，隐藏层130个节点，输出层10个节点，网络结构如图3所示，隐藏层节点及输出层节点激活函数均为logistic函数^[8]。

    即用权值变化量等效磁通量积累（磁通量积累由电压v(t)随时间t的积分得到），对忆阻值即权值进行更新。

2.2 忆阻BP神经网络训练与测试

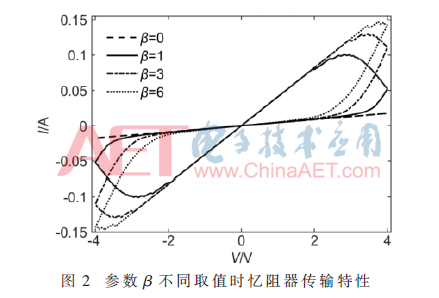
    不考虑忆阻器模型中的参数波动，设参数α=1，β=1，γ₀=-5.9，λ=5.76，对神经网络进行训练及测试，图4为基于MNIST数据集训练的收敛过程，识别率在训练次数超过600次之后变化不显著；训练1 500次之后测试识别率为94.32%。由训练记录数据知，训练次数超过573次之后，模型能够对训练集中超过56 000组数据进行正确的分类，此时测试识别率为93.35%左右，这个结果将作为后续考虑忆阻器性能波动时的对照组。

3 忆阻神经网络稳定性分析

    本节主要分析忆阻器模型中的各个参数波动模拟的忆阻器稳定性问题对忆阻神经网络训练及测试结果的影响，并从忆阻器模型的参数波动回溯到器件结构或性能层次的变化，得到模型参数及器件参量的允许波动范围。

3.1 模型参数与忆阻器件的联系

    本文中忆阻器的忆阻值主要由N=20个相互独立的导电丝中低阻区域和高阻区域的相对长度决定，而低阻区域的初始长度X_i由式(5)、式(6)、式(7)决定：

    参数α、β、γ₀决定X_i的初始长度，但由于γ₀为负指数，β对其调控作用很小，故只考虑参数α和γ₀对X_i的调控。由式(10)可以算出X_i的分布范围为[0.429 4D~0.947 5D]。分析式(8)可知，参数β、λ决定了忆阻器通电之后忆阻值随磁通量的变化速度，参数β、λ越大，忆阻值变化的越快。

3.2 忆阻器参数波动对神经网络的影响

    为了定量地讨论忆阻器稳定性问题对忆阻神经网络的影响，对各个参数设置了不同的波动范围，参数在给定范围内随机取值，记录各种情况下训练中能够对训练集中56 000组数据正确分类时需要的训练次数，并在训练后用测试集数据进行测试。认为训练次数较无参数波动时的573次增加10%，即630次以上时，忆阻器性能波动对网络收敛速度产生显著影响；测试识别率降到90%以下时对网络功能产生显著影响，那么忆阻器的波动就应该限制在该波动程度范围内。

3.2.1 参数α的波动对网络的影响

    参数α是模型中调制导电通道初始长度的参量，初始值为1，对其设置了从±0.001α至±0.3α等多种程度的波动，分别训练多次之后得到各种波动程度下的平均训练次数如图5所示，图中也用散点表示了各种波动时的部分训练次数分布情况。训练完之后对所有情况进行了测试，准确率均在93%左右。

    由图5可以发现参数α的波动程度较小时，训练次数均小于573次，甚至小于450次，也就是说α的小范围波动加快了忆阻神经网络的训练收敛，而且不损失测试准确率。而随着波动程度的增大，训练需要的次数也慢慢增大，最终超过630次，虽然测试准确率仍然是93%左右，但严重影响了网络的收敛速度。

    所以可以得到在不影响忆阻神经网络稳定性的情况下，允许参数α的最大波动范围为±0.22α，即参数α取值应该在0.78~1.22之间。而参数α控制导电丝中低阻部分初始长度X_i，由式(10)可以得到一个忆阻器中X_i值的范围在0.335 2D~1D之间，基于实际忆阻器件即6.704 nm~20 nm之间。

3.2.2 参数β的波动对网络的影响

    参数β是模型中控制忆阻值随磁通量变化速度的参量，也就是影响忆阻神经网络突触权值更新幅度的参量，初始值为1，对其设置了从±0.005β至±8β等多种程度的波动，分别训练多次之后得到各种波动程度下的平均训练次数如图6所示，对各种情况进行了测试，准确率也均在93%左右。

    由图6可以看出，参数β较小程度波动时忆阻神经网络的收敛速度较无波动时快，而波动程度大于±5β之后，训练次数则普遍高于630次，对网络收敛速度产生显著影响，所以β取值范围应该在0~6之间。β主要调控忆阻值随磁通量的变化速度，只能从传输曲线表征，图2为β从小到大变化时忆阻器的传输曲线，忆阻器的传输曲线应该落在β=0和β=6对应曲线之间(其中β=0意味着忆阻器变成定值电阻)。

3.2.3 参数γ₀的波动对网络的影响

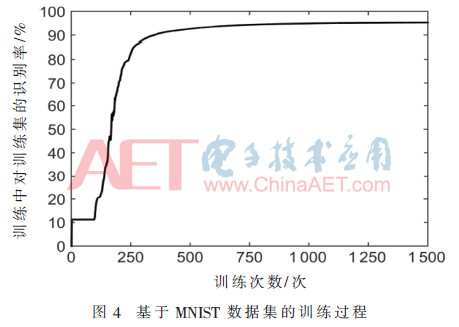
    参数γ₀是模型中对导电通道初始长度进行微调的参量，初始值设为-5.9，对其设置了从±γ₀/20、±γ₀/10至±γ₀/2等多个波动范围，各种情况下忆阻神经网络训练次数如图7所示；训练完之后对所有情况进行了测试，准确率均在93%左右，几乎无损失。

    由图7仍然可以发现参数γ₀的波动程度较小时，忆阻神经网络训练收敛速度较无波动时更快，而且不损失测试准确率；波动程度达到±0.34γ₀以上时，网络训练速度过慢，所以其波动应该控制±0.34γ₀以内，即γ₀取值应该在-7.906~-3.894之间。其调控的X_i的初始值范围应该在0.4283D~0.9641D之间，基于实际忆阻器件X_i的值为：8.566 nm~19.282 nm。

3.2.4 参数λ的波动对网络的影响

    参数λ是模型中最直接控制忆阻值随磁通量变化速度的参量，与参数β的意义相似。初始值为5.76，对其设置了从±λ/10至±9λ等多种波动范围，忆阻神经网络训练次数如图8所示，在波动超过±8.4λ之后训练次数均超过1 000，在图8中用1 000表示。测试准确率保持在92%~93%，几乎无损失。

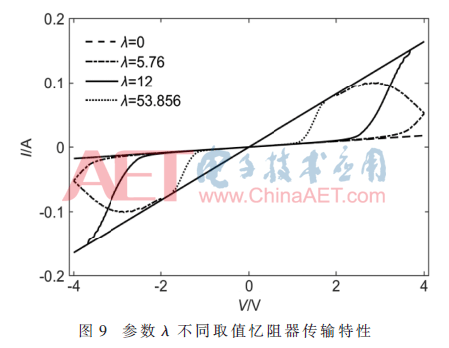
    不难看出，参数λ一定程度内的波动仍然会加快训练收敛速度，但是当波动程度过大之后，训练次数会急剧增加，很快超过1 000次。由训练数据得到：参数λ波动范围在±8.35λ时，平均训练次数为618次，所以参数λ的波动应该控制在±8.35λ以内，这样才能保证忆阻神经网络的稳定性，即参数λ取值在0~53.856之间。λ对忆阻器特性的调控与β相似，从传输曲线上表征。其不同取值时忆阻器传输特性曲线如图9所示，即用作突触的忆阻器的传输曲线应该落在λ=0和λ=53.856对应的曲线之间(其中λ=0意味着忆阻器变成定值电阻)。

4 结论

    本文基于一种等效电阻拓扑结构的忆阻器模型，探究了忆阻器作为神经网络突触时，其不稳定现象对忆阻神经网络的稳定性及功能实现的影响，并得出了基于MNIST手写数据集的忆阻神经网络中忆阻器性能参数在初始设置基础上的最大波动范围：参数α：±0.22α；参数β：±5β；参数γ₀：±0.34γ₀；参数λ:±8.35λ。反映到忆阻器模型中对应的器件参数上，即导电丝(总长度D=20 nm)中低阻部分初始长度Xi应该控制在0.428 3 D~0.964 1 D之间，即8.566 nm~19.282 nm；忆阻值随磁通量的变化速度则从传输曲线上表征。本文的实验结果不仅证实了忆阻器作为神经网络突触结构的可行性，还发现作为突触的忆阻器一定程度内的性能波动会促进神经网络的收敛；此外，器件参量结果也为忆阻神经网络硬件化中忆阻器件的工艺制造和选用提供了一种参考。

参考文献

[1] CHUA L.Memristor-the missing circuit element[J].IEEE Transactions on Circuit Theory，1971，18(5)：507-519.

[2] 王丽丹，段美涛，段书凯.基于STDP规则的忆阻神经网络在图像存储中的应用[J].电子科技大学学报，2013(5)：642-647.

[3] QUERLIOZ D，BICHLER O，GAMRAT C.Simulation of a memristor-based spiking neural network immune to device variations[C].The 2011 International Joint Conference on Neural Networks(IJCNN).IEEE，2011：1775-1781.

[4] KWON D H，KIM K M，JANG J H，et al.Atomic structure of conducting nanofilaments in TiO2 resistive switching memory[J].Nature nanotechnology，2010，5(2)：148.

[5] ZHU R，CHANG S，WANG H，et al.A versatile and accurate compact model of memristor with equivalent resistor topology[J].IEEE Electron Device Letters，2017，38(10)：1367-1370.

[6] YANG J J，PICKETT M D，LI X，et al.Memristive switching mechanism for metal/oxide/metal nanodevices[J].Nature Nanotechnology，2008，3(7)：429.

[7] 黄睿，陆许明，邬依林.基于TensorFlow深度学习手写体数字识别及应用[J].电子技术应用，2018，44(10)：6-10.

[8] 王蒙，常胜，王豪.一种自适应训练的BP神经网络FPGA设计[J].现代电子技术，2016，39(15)：115-118.

作者信息:

田  野，朱若华，汤知日，常  胜

（武汉大学 物理科学与技术学院，湖北 武汉 430072）