0 引言

    在现代战场情景中，空间电磁环境变得日益复杂，使得无人机的探测及其雷达散射截面(Radar Cross Section，RCS)的计算变得更加困难。由于无人机具有“小(低RCS)、慢(速度慢)、低(低飞)”等特点，因此在雷达探测技术中无人机具有较低的探测概率^[1]。同时，无人机的探测概率受复杂地理环境(陆地、城市、海洋等)、气象环境(降雨及云雾等)以及非合作辐射源干扰的影响显著，再加上无人机涂敷吸波材料等造成的隐身性能增强，这样就造成了返回信号的强度极其微弱，返回波形的特征变得复杂。对于雷达系统来说，直接的影响就是影响了其对动态目标的检测和探测，使得现有雷达系统的应用场景受到极大程度的限制^[2]。复杂电磁环境下无人机探测技术成为影响雷达性能的关键制约因素,也是世界性难题。因此在复杂电磁环境下寻求无人机的高效电磁算法，计算目标的RCS，提高雷达的探测性能已成为目前雷达技术发展所面临的一项亟待解决的问题^[3]。

    目前国内外对复杂电磁环境下目标的RCS分析可以分为如下几个部分：

    (1)对目标物的模型进行建立

    在复杂电磁环境中，使用建模软件对目标(飞机、导弹、雷达等)的基本外形和目标本身的复合材料进行建模。再通过软件对上述模型进行计算和分析，主要的兴趣点为目标的电磁吸收和散射等参数。但是通过软件对目标进行建模具有极大的局限性，而目标的形状尺寸等具体参数不尽相同，不同形状的目标其电磁参数也发生了巨大的变化。特别是在电子对抗中，由于被探测的目标具有很高的随机性，因此该方法在电子对抗中的应用较低。

    (2)建立传播模型

    针对于在复杂环境中的电磁波，分析与之对应的电磁波传播衰减模型。诸如文献[4-7]等，国内外已经有大量的学者对此进行了深入的研究。综合上述文章，可以看出，在实际应用中，地理场景、气象场景、非合作辐射场景等是目前的热点，建立在上述情形下的传播模型被当作研究重点。由于建模需要进行运算，因此该方法对计算效率有着很高的要求。

1 复杂电磁环境的定义

    复杂电磁环境特指由于地理因素、气象因素和非合作雷达辐射源等造成的复杂电磁环境。在复杂电磁环境中，雷达回波主要受地理因素、气象因素和非合作辐射源的影响而改变。

    地面、海面等地理因素造成的半空间技术会引起电磁波的强烈反射，这种反射不仅改变了目标的RCS，也将宽带噪声引入到了回波信号中，造成回波信噪比增大，提高了探测难度。

    降雨及云雾等气象因素会对电场波的传播造成不同程度的衰减，大气中水汽凝结物颗粒的大小、几何形状、介电常数和电导率、下降速度、分布特性等都对电磁波的散射和吸收造成不同的影响。

    非合作雷达辐射源照射目标时，通过雷达天线的主波束进入到接收机的双站散射信号和直接通过雷达天线主瓣或副瓣进入雷达接收机的信号对目标回波有着极其复杂的影响。所以，在非合作雷达辐射源干扰背景下检测出目标信号是一个非常困难的问题。

2 复杂电磁环境下无人机等目标的RCS的研究进展

    从1930年以来，采用米氏理论和索末菲积分求解麦克斯韦方程组的解析解被研究人员广泛地使用。但是这种方法有着很大的局限性，它只可以对在规则几何形状中的波传播问题和具有规则结构器件内的平面波传输问题进行求解。从1930年到1960年的初期，许多研究人员通过使用数学上的近似、转化、变换和简化等处理方法来得到麦克斯韦方程组的近似解。采用上述方法，分析电磁学问题的手段和处理应用领域中问题的能力都随之显著提高，但是数学方法的应用范围仍旧有着很大的制约性。虽然基于数学的方法可以极大程度地提高问题的应用场景，得到电磁场问题的精确解，但是仍旧存在着一些问题，如只能求解具有规则边界的简单向题，对任意形状的边界则无能为力或需要很高的数学技巧。由电磁散射理论为基础的麦克斯韦方程可知，可以把电磁散射计算作为边界问题来解。但是精确求解的方法对现实中各种复杂物体的电磁散射问题是无能为力的。

    自1960年，伴随着硬件性能和制作工艺的不断提高和软件编程环境与逻辑的不断优化，同时电磁环境不断变得极其复杂，所以人们需要一种求解方法简洁、计算效率高、有着广泛的应用范围的方法来对目标方程进行直接求解。这就使得一门新兴学科孕育而生——计算电磁学。目前电磁散射计算方法的研究是计算电磁学中最活跃的课题之一，在国内外一直都是研究的热点。各种计算方法包括：高频近似方法、低频数值方法以及关于计算各种媒质散射特性的方法等，都在被广泛研究。在最近的几十年内，随着计算电磁学的发展，已经衍生出多种分析散射问题的方法。

    电磁散射问题的分析方法主要有两种，即高频近似方法、低频数值方法，二者均有其特点和局限。计算RCS的低频方法都是数值方法，按照原理可分为两类：(1)微分方程法，如有限元法和时域有限差分法；(2)积分方程法，如矩量法。有限元法主要可以求解微分方程问题，该方法适应性强，能适应各种形状的边界，但有着计算量大、不适合无界区域、花费时间长等缺点^[8-9]。时域有限差分法对于时域的分析是有效的，但由于计算量大的原因，目前也只能用于电中尺寸物体^[10-13]。作为计算方法中最具代表性的矩量法，它在理论上可以适用于求解任意目标在任意入射场下的散射问题。然而在实际求解过程中，该算法的可行性受到实际情况的限制^[14-15]：一方面，在计算大型目标时，矩量法的矩阵求解复杂度太大，可能会碰到矩阵求逆不收敛的问题；另一方面，在高频区，高频局部散射特性使得目标各部分之间的相互影响较小，从而降低了应用此类过于复杂算法的必要性。

2.1 无人机等目标电磁特征

    目前，探测无人机等目标最主要的手段是使用雷达进行探测。雷达系统在无人机等目标的探测、监视和预警等安全领域有着广泛的适用范围^[2]。但是，因为其主要受复杂背景环境因素的制约，例如：地理因素、气象环境（降雨及云雾等）及复杂运动特性等。而且，由于在目标的设计中采用涂敷吸波材料等方法，使得其隐身性能得到了提高。在复杂背景环境下接受到的雷达回波信号极其微弱、信号的特征极其复杂，使得回波信号的观测性降低，这样直接导致了现有的雷达系统难以满足观测的需求，这也就成为了一个急需解决的问题^[3]。

    目标的雷达回波不仅包括本身，还受复杂探测环境的影响，其中气象因素、地理因素和非合作辐射源对雷达回波造成的干扰较为显著。通过这些背景产生的回波对目标检测产生了不利的影响，这类波被称为背景杂波。本节以海杂波为例进行阐述，进行海杂波中的雷达目标检测技术研究首先要掌握海杂波的特性，但由于受气象、地理等诸多环境因素的影响，海面非线性随机变化，杂波形成机理非常复杂，并且海杂波还与雷达平台、波段、极化、擦地角、高度、分辨率等参数有关。在高海况或低入射角时，还会表现出明显的时变、非高斯、非线性和非平稳特性，使得海杂波特性认知极其困难^[16]。由于目标具有低可观测特性，使得回波信噪比低，增大了雷达检测的难度。

    低可观测特性的目标可以分为多个种类^[1]：(1)由于目标的规模较小（例如小木船等），在探测的过程中导致返回的雷达回波强度很微弱；(2)由于现代国防的需要，目标的隐身技术尤为重要，由于采用了隐身技术，这就使得目标的RCS足够小，为雷达的探测带来了极大的困难；(3)由于目标的尺度足够大，在距离足够远的情形下，基于现有技术的雷达分辨率有限，导致了单元的信噪比降低，制约了雷达技术的发展；(4)由于目标的高速运动，导致了现距离、多普勒走动等现象。以上现象的出现直接导致了导致能量分散^[17-18]。目前，目标等低空飞行器具有“低、慢、小、快、隐”等低可观测性的特性。而且，一些简易航空器容易偏离预定航线和空域，严重威胁民事和军事安全。创新目标检测技术，创建高效电磁计算方法，提高雷达在复杂电磁环境下的目标探测能力是一个迫切需要发展的领域。

    目标RCS的“小”是由于其外形尺寸和材料造成的。当目标外形设计由于空气动力学、任务需求和隐身(低RCS)等约束已达瓶颈时，涂覆隐身材料是有效降低RCS的最有效的措施之一。所以，涂覆目标RCS是目标回波计算中需要关注的关键技术。由于涂覆涂层厚度一般只有几十分之一波长，如果目标尺寸在几十个电波长甚至更长的量级上，那么涂覆目标的电磁散射计算就属于多尺度工程问题。忽略涂层厚度的几何模型会给数值计算的离散化剖分带来很大的困难，同时，在全波算法中会产生奇异的系数矩阵使得算法无法求解。因此，在数值建模时不能因为涂层厚度很薄而忽略。

    文献[19-20]通过引入阻抗边界条件，计算涂覆目标表面的等效反射系数，将等效反射系数带入频域物理光学法的表达式，推导出适用于涂覆目标的时域物理光学法积分表达式并计算涂覆目标的瞬态散射特性，从其等效阻抗边界条件分析可以看出，该方法不适用于极薄层涂覆目标的散射计算。为了解决极薄层涂覆目标的散射计算这一多尺度难题，刘莹等将极薄层边界条件等效阻抗原理应用于多层天线罩的设计研究，解决了多项国防亟需^[21]。此外，在多尺度工程领域，MAO Y R等采用等效阻抗方法解决多尺度电大尺寸问题的计算仿真，并将这一方法用在网状天下无源互调计算中^[22]。

    当目标在“低”飞情况下，地面/海面半空间的强烈反射是造成探测困难的重要原因，这种反射不仅改变了目标的RCS，也将宽带噪声引到回波信号中。雷达接收机工作频段内的非合作辐射源辐射的信号都可以混入到目标的回波信号中，这就与传统单辐射源RCS的分析产生了较大的差别。同时，由于降雨和云雾等气象因素对电磁波的散射和吸收所引起的衰减也不可忽视，而且，不同时频域特性的雷达信号和非合作辐射源信号在回波中的叠加以及气象因素造成的衰减对于信噪比的影响是不同的，这就需要结合三者的时频域特征进行分析。

    无论是地理影响、气象影响，还是非合作辐射源影响，由于目标后向散射信号之间的叠加相位和幅度的互相耦合，产生随机性的特点。为了解决此类问题，需要应用统计电磁学方法，分析回波信号的统计分布规律。

    可以看到，复杂电磁环境下目标的RCS是包含有涂覆目标多尺度计算、气象衰减、多辐射源回波分析方法和统计电磁学等方法，现有商业软件和公开发表文献均无相应结果来验证计算分析的正确性。

    确定性问题的计算电磁学分析技术只能对确定参数下的物理问题进行分析评估，不能模拟和分析该物理问题由于输入参数的随机性而导致的输出量的随机分布问题。统计电磁学是从数学上解空间中的统计概率分布，包括输出解的最大值、最小值和范围，以及输出解的概率密度分布函数，与计算电磁学方法相对应，称之为统计电磁学^[23]。统计电磁学的数值分析方法实际上是计算电磁学与统计方法相结合的方式，工程中可以采用蒙特卡洛数据统计方法结合计算电磁学来分析^[24]。

    在1970年左右，学者们便在实际的电磁工程问题中使用上述方法进行分析和计算，其主要应用场景包括：阵列天线的设计、电磁耦合、复杂结构运算等。这些问题的共同点是它们都是关于多参数是随机取值情形下电磁响应的随机分布。

2.2 地理因素影响下无人机等目标的RCS研究进展

    目前多数雷达系统为了提高识别目标的能力都工作在厘米波、毫米波波段，对于目标来说，其散射性质处于高频区，满足高频近似的要求。同时，由于低频方法受到存储量和运算时间的限制，因此在实际工程应用中，大都将高频近似方法作为复杂目标RCS评估软件所采用的主要方法。西安电子科技大学李晓峰等在半空间环境下的目标特性进行过深入研究，做了大量的原创性工作^[25-28]。文献[25-28]将半空间并矢格林函数引入传统的物理光学方法，在等效电磁流方法中，对半空间复杂目标面元和棱边的电磁模型进行计算处理。同时结合图形电磁学，对半空间目标进行消隐处理，提取单位象素面元法矢量和深度值等有效信息，与地面反射波对目标的二次照射贡献相叠加，得到半空间电大目标的雷达散射截面。在此基础上，进一步展开对半空间介质、涂覆目标的电磁散射特性进行分析。研究结果表明，目标在半空间环境下对入射电磁波的调制效应与独立目标存在时的调制效应大大不同。

    如图1所示，与高空目标所处的自由空间相比，海面/地面半空间的反射会造成低飞飞弹、地面车辆或海面舰船等目标的回波相互作用。这种相互作用，在频率域中来看，造成其单个频点上的RCS值的显著变化。其中，E^inc和H^inc是入射的电场和磁场强度，E_S和H_S是散射的电场和磁场强度，E_Swedge和H_Swedge是棱边散射的电场和磁场强度，E_Sface和H_Sface是散射体面上的电场和磁场强度，E_Sref和H_Sref是半空间多重散射场。

    目标-半空间之间的多次相互作用很难用射线方法进行分析，一般采用半空间格林函数方法进行分析，将土壤(或海水)的电磁参数和目标距离半空间的高度等信息等效进半空间格林函数，高效地评估半空间地理信息对于目标回波的影响。

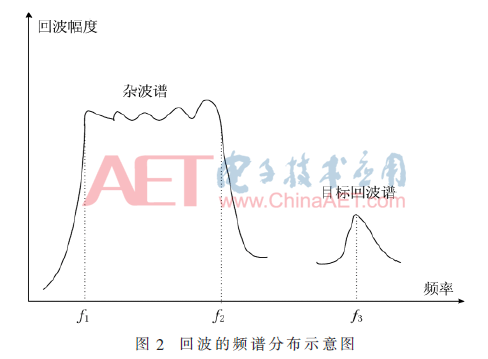
    实际上，地面和海面是起伏的粗糙表面，这种粗糙表面的强烈反射会从雷达天线的主瓣和副瓣进入雷达接收机。如果雷达探测平台具有一定的相对运动性，则产生的回波中的噪声是一个具有很宽频谱带宽、很强幅度的噪声信号。相对而言，信号回波频谱的幅度很低，如图2所示，如果没有相对的多普勒频率差异，很容易陷入噪声中无法检测，而当具有足够的多普勒频差时，目标的观测则相对容易很多。

2.3 气象因素影响下目标RCS的研究进展

    气象因素对电磁波的传输、散射、衰减特性与应用的影响的研究一直都受到国内外学者的关注。VAN VLECK J H在20世纪40年代就对此问题展开了研究，并用量子理论推导出电波被氧气吸收最通用的表达式，研究结果表明在吸收线附近频率电波衰减的计算结果与测量结果一致，但是，频率较远时其电波衰减却差别较大^[29]；20世纪50年代，GROSS B在VAN VLECK J H研究的基础上作了进一步研究，得到了离吸收线较远频率处与测量更吻合的结果^[30]。1975年ROSENKRANZ H S在VAN VLECK J H和GROSS B公式的基础上提出了修正后的计算公式，使电波衰减的计算值与测量值更吻合^[31]。直到1985年，用温度、压强和水汽压三要素表示大气吸收的公式才被LIEBE H J提出，用该公式得到的计算结果与测量结果能较好吻合，并且该公式已被CCIR所采用^[32]。近年来，我国也结合历年探空数据得开展了适合各地区的大气吸收模型的相关研究，分析了吸收率的高度剖面分布和地域分布特点^[33]。1990年SALONEN E等提出了适用于干空气中，频率低于60 GHz电磁波在倾斜路径的电波衰减预报模型^[34]，1993年形成了MPM计算模型。1998年ITU-R提出了计算晴空大气对电波衰减的预报模型^[35]。

    在降雨对电波传播的影响的研究中，一般将雨滴外形视作球形来研究，采用Mie理论计算雨滴的散射截面和吸收截面，并应用于对电波的衰减的研究中^[33，36-37]。有时为了更真实地描述雨滴的外部形状，将雨滴视为扁椭球状或者底部有一凹槽的扁椭球状的Pruppacher-Pitter型雨滴^[38]，并伴随产生了计算其散射特性的各种方法，如点匹配法、Fredholm积分法等^[36，39-40]，并在此基础上对不同极化和不同频率电波的降雨衰减和雨致去极化进行了广泛的研究，得到了不同频率雨致特征衰减与降雨率的指数关系^[41-43]，在大量实验数据的基础上得到了较多的雨衰模型和去极化模型。

    云层对电波衰减的影响研究主要体现在毫米波波段。LHERMITTE R M做了毫米波多谱勒雷达对云和降水的观测实验后证明94 GHz的毫米波多普勒雷达能用于气象观测，而且具有优良的多普勒特性^[44]，并能有效观测云边界及初始阶段的云。ALTSHULER E E和MARR R A采用工作在15 GHz和35 GHz的雷达，测量了Boston地区有云覆盖条件下的整个大气衰减^[45]。DINTELMANN F和ORTGIES G提出了一种云衰减全年累积统计预测的半经验模型，并由辐射计测量得到了模型参数^[46]。ORTGIES G等报告了卫星链路在20 GHz和30 GHz时晴空大气的衰减特性^[47]。DAVIES O T等把无线电探空得到的云衰减模型和一年的93 GHz无线电探测仪测量的云衰减结果进行了比较，发现两者衰减一致^[48]。DISSANAYKE A等提出了在SHF(3～30 GHz)和EHF(30～300 GHz)频段的全球可用的云衰减模型^[49]。

    以上虽然给出了一些降雨和云层对电波衰减的模型，但都很难得到具体地域（位置）的气象数据和测量结果，因此需要研究不同地域的降雨和云层的分布情况，由于降雨和云层受季节和气候影响较大，因此已有衰减模型还需在不同地区及不同气候条件下进行深入的实验和理论研究。

2.4 非合作雷达辐射源对无人机等目标RCS影响的分析方法

    非合作雷达辐射源对目标雷达回波的影响主要体现在辐射源照射无人机的情形，其双站散射信号进入雷达主波束，或非合作辐射源的辐射信号直接通过雷达天线方向图主瓣或副瓣进入雷达接收机，对雷达自身发射的电磁波对目标照射产生的回波造成的影响。

    在非合作雷达辐射源识别动目标指示功能方面，SCHOENENBERGER J G和FORREST J R在1982年开发出了使用独立接收机的民用机场交通管制双多基地雷达系统^[50]。而不用直接接收雷达发射信号就可实现动目标指示功能的方案在1984年被GRIFFITHS H D和CARTER S M提出^[51]。YAMANO L C等人在1984年申请了具有在接收雷达信号中补偿遇到的相位变化的相干雷达接收机的专利^[52]。美国Technology Service公司的THOMPSON E C在1989年发表的论文中提出了利用预警机作为非合作辐射源来发现和检测飞行目标，利用联合监视目标攻击雷达系统作为非协同照射源来发现和检测地面目标的方案^[53]。

    在非合作辐射源对目标的威胁性方面，美空军实验室在2001年的一项研究报告中意识到了无源雷达系统对非合作雷达辐射源的威胁性，并增加了敌方探测的难度，从而削弱了无源雷达系统探测的能力^[54-55]。在美国2005年与2007年召开的雷达会议上，OLSEN K E等人利用L波段民用空中交通管制雷达作为非合作辐射源, 接收机采用单个全向天线接收非合作雷达辐射源的直达波和目标散射回波绘制了目标航迹^[56-57]。

    总之，目前对非合作雷达辐射源在无人机等目标无源相干检测及定位等核心技术上取得了一定进展，但对于非合作辐射源对目标有源雷达回波干扰的影响未曾有报道，仍处于探索研究阶段。

    非合作辐射源对雷达回波造成的影响应从非相干干扰和相干干扰方面分别分析。如果非合作雷达辐射源产生的目标回波到达雷达接收天线的信号与雷达主动辐射信号的回波信号呈现稳定的相位关系，则非合作雷辐射源对雷达回波产生相干干扰，如果不能保持稳定的相位关系，则产生非相干干扰。

3 结论

    本文针对于无人机等目标在复杂电磁环境下的 “小、慢、低”特性，给出了地理因素、气象因素、非合作雷达辐射源等复杂电磁环境的特征以及对无人机目标回波特性的影响。通过对半空间雷达散射截面、气象因素对电波衰减的影响及非合作雷达辐射源对雷达回波造成的影响，介绍了复杂电磁环境下无人机雷达散射截面的研究进展。

参考文献

[1] 陈小龙，关键，董云龙，等.稀疏域海杂波抑制与微动目标检测方法[J].电子学报，2016，44(4)：860-867.

[2] 杨建宇.雷达技术发展规律和宏观趋势分析[J].雷达学报，2012，1(1)：19-27.

[3] 何友，黄勇，关键，等.海杂波中的雷达目标检测技术综述[J].现代雷达，2014，36(12)：1-9.

[4] ENGEL K，HADWIGER M，KNISS M J，et al.Real-time volume graphics[M].Wellesley MA：A K Peters，Ltd，2006.

[5] 魏岳江.复杂电磁环境下的联合训练[J].国防科技，2008，29(4)：62-67.

[6] 周海飞，尤峰.对提高复杂电磁环境下装甲机械化部队通信训练质量的思考[J].兵工自动化，2008，27(1)：61-62.

[7] 孙国至，刘尚合.电磁环境效应内涵研究[J].中国电子科学研究院学报，2010，5(3)：260-263.

[8] ZIENKIEWICZ O C，TAYLOR R L.The finite element method 4th[M].New York：McGraw-Hill，1989.

[9] NORRIE D H，VRIES G D.The finite element method: fundamentals and applications[M].London：Academic Press，1973.

[10] YEE K S.Numerical solution of initial boundary value problems involving Maxwell's equation in isotropic media[J].IEEE Transactions on Antennas and Propagation，1966，14(5)：302-307.

[11] TAFLOVE A，HAGNESS S C.Computational electrodynamics：the finite-difference time-domain method 3nd[M].Norwood，MA：Artech House，2005.

[12] TAFLOVE A.Advances in computational electrodynamics：the finite-difference time-domain[M].Boston：Artech House，1998.

[13] TAFLOVE A.Review of the formulation and applications of the finite-difference time-domain method for numerical modeling of electromagnetic wave interactions with arbitrary structures[J].Wave Motion，1988，10(6)：547-582.

[14] HARRINGTON R F，MAUTZ J R.Theory of characteristic modes for conducting bodies[J].IEEE Transactions on Antennas and Propagation，1971，19(6)：622-628.

[15] HARRINGTON R F.Field computation by moment methods[M].New York：McGraw-Hill，1968.

[16] 许稼，彭应宁，夏香根，等.空时频检测前聚焦雷达信号处理方法[J].雷达学报，2014，3(2)：129-141.

[17] 牛立强，谢拥军，张春刚，等.对抗环境下宙斯盾系统探测弹道导弹的仿真[J/OL].系统工程与电子技术[2019-05-16].http：//kns.cnki.net/kcms/detail/11.2422.TN.20190305.1146.006.html.

[18] Niu Liqiang，Xie Yongjun.A radar simulation system based on the path files[C].2016 IEEE International Conference on Ubiquitous Wireless Broadband.Nanjing，China，2016：16-19.

文献[19]-[57]略

作者信息:

向  敏1，牛立强2，武沛羽2，谢拥军2，石宋华1，严  杰1

(1.航空工业成都飞机工业(集团)有限责任公司，四川 成都610000；2.北京航空航天大学 电子信息工程学院，北京100083)