0 引言

    超材料，一种新型的三维周期性人工电磁材料，通常由金属/介质或全介质构成，在微波、太赫兹波段，由于其比拟波长的单元结构与电磁波的电场或磁场的共振效应，这种操控电磁波的特殊能力在过去十年中得到了广泛的研究，如完美吸收器^[1-3]、隐身^[4-6]、散射减少^[7]等。然而，在微纳米尺度下，超材料的应用由于高损耗和三维制造的困难受到阻碍和限制。超表面是具有亚波长厚度的二维平面超材料，与三维超材料相比，超表面具有物理尺寸更小、易制造、损耗更低等优势，因此，在很多应用领域下，超表面可以代替更大体积的三维超材料结构。近些年，超表面巨大的应用潜力受到全世界研究人员的关注，包括偏振转换器^[8-9]、平面透镜^[10]、涡旋相位板^[11]、数字编码超表面^[12]和全息成像^[13]等。

    电磁波波前的可调性在于其相位的调控，根据费马原理，电磁波的跃迁是相位沿传播路径的积累效应。因此，用于控制波前的传统光学元件需要空间变化的折射率或其整体几何形状的改变来实现相位积累。然而，由于自然材料的介电常数有限性，通常采用弯曲表面来实现(由于其体积大、重量大、设计过程复杂)，这已经成为现代电光系统集成和小型化需求日益增长的障碍。因此，在微纳米尺度上实现电磁波的相位控制已成为现代光学和微纳米光学发展的关键。

    梯度超表面指的是一种能够使入射电磁波与厚度可忽略的周期性元胞阵列产生共振响应，并能使其入射波相位发生突变的亚波长结构。这种基于相位梯度变化的超表面，可以使得在超表面分界面上的反射波或者透射波的传播方向发生异常折射或者偏转。在2011年，哈佛大学CAPASSO F等人在研究相位不连续性在对电磁波的调控能力上，提出了广义斯涅尔定律并给出了相应的理论推导^[14]，发表在了《Science》期刊上。早些年，在光波段异常的折射和反射，无法用传统的斯涅尔折射反射定律加以解释。CAPASSO F教授团队从概念和应用的角度出发，对传统的斯涅尔定律进行扩展后，这一扩展后的定律不仅对电磁波的异常出射能够作出完美的解释，并且为电磁波波前调控领域提供了新的思维方式，对电磁波调控器件和平面太赫兹光学器件的应用开辟了一条新的道路。

    本文概述了几种典型的梯度超表面领域的重要器件，从超表面的相位调控设计方法出发，总结了其各自的原理和应用，继而对下一步超表面的发展及应用展望。

1 原理简介

1.1 广义斯涅耳定律

    2011年，CAPASSO F教授团队首次在两种介质界面处引入了突变相移，从一维角度出发，给出了基于费马原理异常折射和反射的推导，提出了广义的斯涅尔定律^[14]。在两个介质交界面构成的超薄的超表面，它会给入射波提供线性梯度的相位突变，从而引入与位置相关的相移Φ(x)，如图1所示。       

    考虑电磁波入射角度θ_i，两种异常反射和折射定律可写为：

1.2 Pancharatnam-Berry相位

    超表面的相位或幅值可以基于单元结构的几何形状的变化而改变，Pancharatnam-Berry相位(P-B相位)指的是通过调整具有相同几何形状的单元结构的方向角来实现相位控制^[15-16]，如图2所示。在电磁波正入射下，圆极化波（CP）偏振方向沿微结构两个主轴方向时，以x轴作为起始轴，当微结构以θ旋转一个角度时，出射波会有一个相位增量(±i·2^θ)，并且该出射波的手性与原入射波的手性相反。因此，这种绕微结构中心旋转的方法能够有效地满足2π相移的全覆盖，该相位调制方法能够有效实现对电磁波的调控。

2 超表面器件与应用

2.1 可编程数字超表面

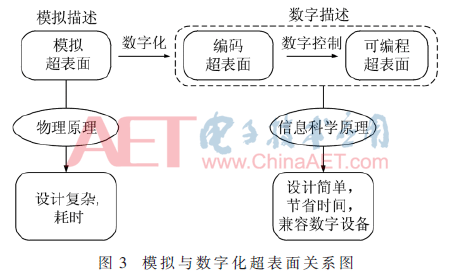
    现阶段对信息超表面的研究主要包括3类，如表1所示。连续的媒质参数可用来描述传统的超表面（模拟超表面），这种宏观均匀的描述方式不能很好地完全等效。2014年，“编码超表面”、“可编程超表面”等新颖的概念相继提出^[12]，崔铁军教授团队通过采用数字化控制的手段，0°相位响应的微单元模拟“0”二进制数字态，而180°对应“1”数字态，实现对电磁波的数字化调控。

    相比与传统的超表面，数字编码式超表面在设计上具有巨大的优势，如图3所示。在电磁波调控领域，其设计简单，操作灵活。

2.1.1 各向同性编码超表面

    超表面在编码上的调控与相控阵理论相近^[12]：对超表面进行单元格划分(M×M)，表征“0”或“1”的数字码填充到每一个单元格，阵列的方向性系数可写成：

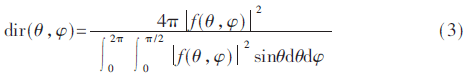
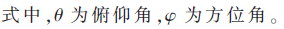
    目前，二进制两种状态的编码方式在设计上最为简单，而且多为反射式，由于各向同性超表面偏振不敏感性，在降低散射上应用广泛^[17]。2015年，崔铁军教授课题组提出了基于圆环型结构1-bit反射式编码超表面^[18]，如图4(a)所示。图4(b)展示了在0.4～1.8 THz宽频带下，可以实现编码“1”和“0”反射相位差近似180°。

    此种1-bit反射式编码超表面在0.80~1.4 THz的宽频率范围内，反射率小于-10 dB，且对入射波的偏振不敏感，在太赫兹波宽频率范围内实现空间漫反射，在降低领域发挥巨大作用。

    在太赫兹波段，范围广多角度的电磁波束的调控需要多bit的编码形式，图5（a）为一种新颖的方形环凹口状结构的2-bit反射式的编码超表面^[17]，同样由于结构具有对称性，能够使不同极化方向上的入射波向空间各处位置反射，这种多bit编码方式的多种选择，能够有效地分散能量分布，为有效控制太赫兹波漫反射提供有效途径。

2.1.2 各向异性编码超表面

    2016年，另外一种各向异性编码的电磁波调控方式继而提出^[19]，不同的偏振方向产生不同的相位分布，即有不同功能的波束调控模式，如图6所示。

    微单元由哑铃型和方片型结构组成，对于不同的偏振，表面的相位分布呈现方格和光栅条纹排布，x偏振下，入射波反射为四个对称外朝向的对称波束，而在y方向上，反射为两个对称朝外的铅笔波束^[12，20]。

    此种多bit各向异性编码超表面在多功能器件上有很好的应用前景，双极化特性可以将波形偏转和分束有效结合起来实现对电磁波的有效控制；在太赫兹波通信领域，多极化调制的太赫兹波信号可以增加信息容量，有效提高传输通信速率；此外，双极化图像编码在数字化全息成像领域拥有巨大发展潜力。

2.2 涡旋波束

    涡旋波束是一种具有环形剖面强度和螺旋式相位波前并且携带轨道角动量(OAM)的波束^[21]。θ可用表达式exp（ilφ）表示，即有相位因子θ=ilφ，其中φ为与传播方向垂直平面的旋转方位角，拓扑电荷数l为在一个波长内扭转的次数。轨道角动量L可用方程L=lh，h是普朗克常数。

    在太赫兹波频率范围，尺寸的急剧小型化使得传统的大尺寸阶梯型螺旋相位板不再适用；天线阵列馈电网络的复杂性也限制了涡旋波束的应用。而在人工电磁超表面旋转方位的剖面上附加共振^[22]或P-B变化的相位^[23]，通过灵活的调控相位方式，有效地实现涡旋波束的产生。

    目前在人工超表面激发涡旋波束的方式主要分为3类，如表2所示。

2.2.1 线极化波激发涡旋波束

    2011年，哈佛大学Yu Nanfang和GENEVET P等人在广义斯涅尔定律基础上利用V型微结构相位共振特性在超表面上划分8个相位差为π/4区域，实现了±1阶涡旋波束，发表在《Science》期刊上^[14]，如图7所示。之后基于各种结构(包括C型、U型、L型等)的超表面产生涡旋波束的研究得到了迅猛的发展^[24]。

    V型微结构在线性极化波的激励下，可以产生对称与非对称两种共振模式，如图8所示。由于两种共振方式的耦合能够有效地覆盖0~2π的相移，有利于电磁波相位调控。

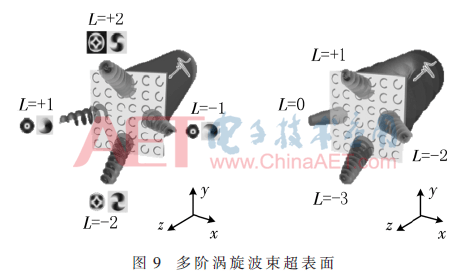
    此种按照环形区域划分相位的设计方法简单，易于加工，图9为多阶涡旋波束产生方式^[25]，涡旋波束各个模式彼此正交，对于无线通信中提高频谱利用率增大信息容量具有重要意义。

2.2.2 圆极化波激发涡旋波束

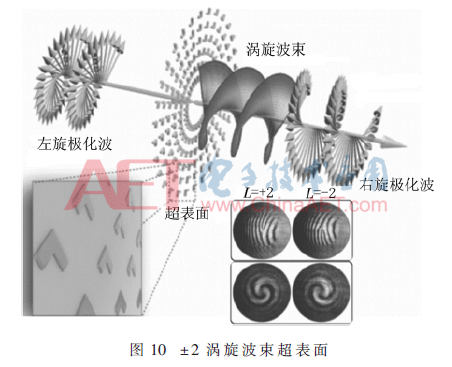
    基于P-B相位原理的高阶涡旋波束产生方法相对于共振形式而言，设计上更为简单，通过旋转单元结构方向角即可实现。图10展示了一种±2阶涡旋波束产生方法^[11]，超表面阵列按照环形旋转单元结构方位角覆盖2π，方向角相位覆盖4π，在左右旋圆极化波入射下可实现拓扑电荷数L为±2涡旋波束。

2.2.3 等离子体表面波激发涡旋波束

    2018年，上海理工大学庄松林院士团队和澳大利亚墨尔本大学合作利用表面等离子波在太赫兹涡旋波束轨道角动量的调控取得了突破性的进展^[26]，如图11所示。

    在金属薄膜上刻蚀矩形狭缝结构，并且按照圆环形方式排列，通过调整空气狭缝的几何相位，实现了圆极化波入射下任意轨道角动量拓扑电荷数的调控，这种方法在未来太赫兹通信、轨道角动量调控等应用拥有巨大的潜力。

2.3 平面超透镜

    传统的透镜是通过空间相位的积累实现对入射波的聚焦，因而表面不同相位分布需要靠材料的厚度来调节，呈现出非均匀且有一定厚度的特性。相比之下，基于超表面的透镜可以在厚度可忽略不计平面上实现入射波的相位调制，从而大大减小透镜的尺寸。为了实现聚焦，超表面通常将入射平面波前重塑为球面波前^[27]。平面透镜上各点的相移与其位置之间的关系为：

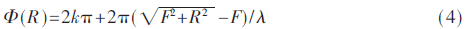
式中，Φ是突变相位，F是透镜焦距，R为透镜的径向向外分布的距离。目前，平面超透镜根据材料可调谐性可以分为两类，如表3所示。

2.3.1 静态平面超透镜

    静态平面超透镜一般由单层或多层微结构阵列构成。2015年，天津大学张伟力教授团队提出的一种带宽0.4 THz平面超透镜^[28]，如图12所示。基于共振相位的C型单层金属结构，能够有效地覆盖2π相移，并且阵列单元结构透射率能稳定在0.5左右。

    这种基于单层或多层金属的平面超透镜在可以在满足相位调制的前提下，可实现波束的宽带聚焦^[29]等多种功能。这些静态平面透镜在可以在激光显微镜、成像和光谱学中得到广泛的应用。

    图13展示了多焦点平面透镜^[30]。基于几何相位调控的自旋选择平面透镜，采用的是狭缝天线作为单元结构，可将不同自旋态的入射波聚焦到宽频带范围内的两个分离焦斑上，实现多焦点聚焦。这种多焦点平面镜在为开发紧凑型成像系统和光电子设备提供前景。

2.3.2 可调谐平面超透镜

    可调谐平面超透镜主要是通过二维材料、相变特性材料来实现平面超透镜的功能调谐^[31-33]。石墨烯超透镜是通过将活性石墨烯与金属或介电质超表面相结合，或直接利用石墨烯结构作为超表面的材料来控制波前。

    图14(a)展示了一种基于石墨烯的可调谐反射聚焦透镜^[31]，该透镜由矩形孔径阵列构成。通过调节石墨烯费米能级，继而动态地调节其表面离子体激元的光学性质，从而导致反射光的相位突变。其可以实现太赫兹圆极化波的焦点强度或焦距的动态调控，焦点动态范围可达44 μm。

    基于二氧化钒(VO₂)的相变材料可通过光控实现金属态和介质态的转换，采用VO₂的动态全息表面^[32]和采用介质硅设计的偏振开关^[33]都很容易地扩展基于超表面的有源平面光学组件，在光敏自动对焦相机的超快变焦平面透镜应用中具有巨大的潜力。

2.4 全息成像

    1948年，全息成像技术是由GABOR E D提出的，通过照射在全息图(一种光学记录的干涉图样)后的散射波束，重建物体的三维成像^[34]。此后,全息成像在计算机可重构的帮助下获得广泛应用，例如可重构调节的空间光调制器(SLMs)^[35]。而超表面对相位的灵活操控使得全息成像技术进一步得到发展，结合Gerchberg-Saxton迭代算法的太赫兹全息相位板^[36]在3D数字成像、记忆存储、太赫兹光学信息传输、半导体载流子输运等应用上具有非凡的应用价值。

3 总结与展望

    超表面是替代传统电磁元件的最有前途的选择之一，更适用于高集成度的微型化光电器件。在太赫兹波段下，效率作为关键性能因素之一，现有超表面的效率还需要进一步提高。由于半导体或高折射率介质在较长的波长内损耗较小，特别是全介质硅超表面应用广泛，为了实现有源超表面，如采用相变材料、二维材料、液晶等来实现可调性能。此外，从实际应用的角度来看，在柔性衬底上制备的超表面具有广泛的应用价值。

    在过去的几年里，超表面器件发展迅速，但是在器件集成和进一步减小损耗上要找到一个令人满意的、完整的解决方案仍然有很长的路要走。在可预期的未来，超表面器件将会发挥更大的实际应用价值，这也将推动着太赫兹光学系统的集成的发展。

参考文献

[1] LANDY N I，SAJUYIGBE S，MOCK J J，et al.Perfect metamaterial absorber[J].Physical Review Letters，2008，100(20)：207402. 

[2] LI W，VALENTINE J.Metamaterial perfect absorber based hot electron photodetection[J].Nano Letters，2014，14(6)：3510-3514.

[3] HAO J，WANG J，LIU X，et al.High performance optical absorber based on a plasmonic metamaterial[J].Applled Physics Letters，2010，96(25)：251104.

[4] SCHURIG D，MOCK J J，JUSTICE B J，et al.Metamaterial electromagnetic cloak at microwave frequencies[J].Science，2006，314(5801)：977-980.

[5] ALU A，ENGHETA N.Achieving transparency with plasmonic and metamaterial coatings[J].Physical Review E，2005，72(1)：016623.

[6] CAI W，CHETTIAR U K，KILDISHEV A V，et al.Optical cloaking with metamaterials[J].Nature Photonics，2007，1(4)：224-227.

[7] MODI A Y，BALANIS C A，BIRTCHER C R，et al.Novel design of ultra-broadband radar cross section reduction surfaces using artificial magnetic conductors[J].IEEE Transaction on Antennas & Propagation，2017，65(10)：5406-5417.

[8] ZHOU L，ZHAO G Z，LI Y H.Broadband terahertz polarization converter based on l-shaped metamaterial[J].Laser & Optoelectronics Progress，2018，55(4)：041602.

[9] CAO J G，ZHOU Y X.Polarization modulation of terahertz wave by graphene metamaterial with grating structure[J].Laser & Optoelec，Tronics Progress，2018，55(9)：092501.

[10] FANG N，LEE H，SUN C，et al.Sub-diffraction-limited optical imaging with a silver superlens[J].Science，2005，308(5721)：534-537.

[11] KARIMI E，SCHULZ S A，DE LEON I，et al.Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface[J].Light：Science & Applications，2014，3：e167.

[12] CUI T J，QI M Q，WAN X，et al.Coding metamaterials，digital metamaterials and programmable metamaterials[J].Light：Science ＆ Application，2014，3：e218.

[13] WEN D，YUE F，LI G，et al.Helicity multiplexed broad-band metasurface holograms[J].Nature Communications，2015，6：8241.

[14] Yu Nanfang，GENEVET P，KATS M A，et al.Light propagation with phase discontinuities：generalized laws of reflection and refraction[J].Science，2011，334(6054)：333-337.

[15] HUANG L，CHEN X，MUHLENBERND H，et al.Dispersionless phase discontinuities for controlling light propagation[J].Nano Letters，2012，12(11)：5750-5755.

[16] JIANG S C，XIONG X，HU Y S，et al.High-efficiency generation of circularly polarized light via symmetry-induced anomalous reflection[J].Physical Review B，2015，91(12)：125421.

[17] GAO L H，CHENG Q，YANG J，et al.Broadband diffusion of terahertz waves by multi-bit coding metasurface[J].Light：Science ＆ Application，2015，4(9)：e324.

[18] LIANG L J，QI M Q，CUI T J，et al.Anomalous Terahertz reflection and scattering by flexible and conformal coding metamaterials[J].Advanced Optical Materials，2015，3(10)：1374-1380.

[19] LIU S，CUI T J，XU Q，et al.Anisotropic coding metama-terials and their powerful manipulation to differently polarized terahertz waves[J].Light: Science ＆ Application，2015，5(5)：e16076.

[20] PAQUAY M，IRIARTE J C，EDERRA I，et al.Thin AMC structure for radar cross-section reduction[J].IEEE Transactions on Antennas and Propagation，2007，55(12)：3630-3638.

[21] ALLEN L，BEIJERSBERGEN M W，SPREEUW R J，et al.Orbital angular momentum of light and transformation of laguerre gaussian laser modes[J].Physical Review A，1992，45(11)：8185-8189.

[22] GENEVET P，YU N，AIETA F，et al.Ultra-thin plasmonic optical vortex plate based on phase discontinuities[J].Applied Physics Letters，2012，100(1)：013101.

[23] YUE F，WEN D，XIN J，et al.Vector vortex beam generation with a single plasmonic metasurface[J].ACS Photonics，2016，3(9)：1558-1563.

[24] KARIMI E，SCHULZ S A.Generating optical orbital angular momentum at visible wavelengths using a plasmonic meta-surface[J].Light：Science & Applications，2014，3：e167.

[25] ZHAO H，QUAN B G.Demonstration of orbital angular momentum multiplexing and demultiplexing based on a metasurface in the terahertz band[J].ACS Photonics，2017，5(5)：1726-1732.

[26] ZANG X F，ZHU Y M，MAO C X，et al.Manipulating terahertz plasmonic vortex based on geometric and dynamic phase[J].Advanced Optical Materials，2018，7(3)：1801328.

[27] SUN J，WANG X，XU T，et al.Spinning light on the nanoscale[J].Nano Letters，2014，14(5)：2726-2729.

[28] WANG Q，ZHANG X，XU Y，et al.A broadband metasur-face-based terahertz flat-lens array[J].Advanced Optical Materials，2015，3(6)：779-785.

[29] YANG Q，GU J，XU Y，et al.Broadband and robust metalens with nonlinear phase profiles for efficient terahertz wave control[J].Advanced Optical Materials，2017，5(10)：1601084.

[30] WANG S，WANG X，KAN Q，et al.Spin-selected focusing and imaging based on metasurface lens[J].Optics Express，2015，23(20)：26434-26441.

[31] DING P，LI Y，SHAO L，et al.Graphene aperture-based metalens for dynamic focusing of terahertz waves[J].Optics Express，2018，26(21)：28038-28050.

[32] LIU X B，WANG Q，ZHANG X Q，et al.Thermally dependent dynamic meta-holography using a vanadium dioxide integrated metasurface[J].Advanced Optical Materials，2019(4)：1-7.

[33] LONGQING C，KUMAR S Y，HUIFANG Z，et al.Alloptical active THz metasurfaces for ultrafast polarization switching and dynamic beam splitting[J].Light：Science & Applications，2018，7：28.

[34] GABOR E D.Character recognition by holography[J].Nature，1948，208：422-423.

[35] LAZAREV G，HERMERSCHMIDT A，KRUGER S，et al.Optical imaging and metrology：advaneed technologies[M].Wiley-VCH，Weinheim，Germany，2012.

[36] HU D，WANG K X.Ultrathin terahertz planar elements[J].Advanced Optical Materials，2013，1(2)：186-191.

作者信息：

寇  伟1，陈  婷1，杨梓强1，梁士雄2

(1.电子科技大学 电子科学与工程学院，四川 成都610054；

2.中国电子科技集团公司第十三研究所 专用集成电路重点实验室，河北 石家庄050051)