文献标识码: A
DOI:10.16157/j.issn.0258-7998.2018.S1.016
0 引言
随着电网的发展以及电力系统规模的扩大以及分布式电源的兴起,电网运行越来越接近于极限状态,重载运行的电网出现越来越多的快速或慢速的电压跌落现象,严重的导致电压崩溃,因此电压稳定问题已成为电力系统规划、运行的重点[1]。由电压失稳发展成电压崩溃并扩大为全网性事故的风险也随着电压稳定问题的日益严重而增加,从而影响到电力系统的安全稳定和经济运行。电力系统运行的实践与理论研究已证明,通过向电力系统的重要枢纽点提供快速的动态无功电压支撑,能有效解决电力系统安全稳定问题。在电力系统中的电压水平由无功功率的平衡决定,使用静止无功补偿器可以快速提供所需的动态无功功率,稳定系统电压,防止系统电压崩溃[2]。
静止无功补偿器(Static Var Compensator, SVC)是灵活交流输电系统的重要组成部分,能够提供连续可调的感性或容性无功,对电网中的无功负荷实时跟踪补偿,维持平稳的电压控制,提升远距离传输容量。SVC不仅可以改善电力系统的静态、暂态稳定[3],降低瞬时过电压,还可以通过附加控制抑制电力系统的功率振荡,阻尼电力系统的次同步谐振/振荡,从而改善提高电力系统的稳定运行范围[4]。由于静止无功补偿器具有快速平滑调节、运行可靠、可分相调节,利用静止无功补偿器改善系统电压质量和提高电力系统在小干扰和大干扰下的稳定性已获得较为广泛的应用[5]。
1 电压稳定机理
电压稳定性是指电力系统在正常运行情况下或遭受扰动后,电力系统维持负荷点母线电压或恢复到允许的范围内,不发生电压崩溃的能力。
如果发生了某些干扰,如负荷增加或系统状态变化过大,引起电压不可控地增高或下降时,系统会脱离平衡点,进入电压失稳状态。导致电压失稳的主要原因通常是电力系统缺少无功功率调节能力。
假设有功功率恒定,对应的电压-无功功率特性曲线上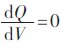 位置是系统电压稳定的临界点,也可称为电压失稳点,而当
位置是系统电压稳定的临界点,也可称为电压失稳点,而当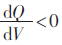 时,在此位置附近受到小的扰动后系统电压能自动恢复稳定平衡。
时,在此位置附近受到小的扰动后系统电压能自动恢复稳定平衡。
假如在某个全局或局部的重大扰动作用下,系统电压在短时间内不可逆地持续下降,系统电压稳定性破坏,最终导致大面积停电,电力系统负荷节点的电压失去稳定后急剧下降的后果就是电压崩溃。系统电压失稳后可能导致电压崩溃,电压崩溃可以是局部的或全局的。
有功功率和无功功率二者同时对电压稳定有重要的作用。在交流网中,电抗线路占主导,电压控制和无功功率有密切的关系。缺少无功功率不仅会引起电压降低,还影响到电压稳定,甚至可能引起电压崩溃。
对于以电抗线路占主导的电网,在正常运行情况下,可以近似认为随着注入该母线的无功功率的增加,母线电压的幅值升高。如果系统中有至少一个母线电压的幅值随着注入该母线的无功功率的增加而降低,则整个系统是电压不稳定的。这显然和通常对于提高母线电压所采取的无功补偿控制措施是相一致的。
按采用的模型,电压稳定性研究可划分为两大类:基于微分方程的动态研究和基于潮流方程的静态研究。本质上电力系统运行过程是动态的,所有的动态元件都对系统电压稳定有影响。一般通过电压失稳不同的表现形式分析:
(1)静态电压稳定
静态问题一般是指电力系统传输功率达到最大时的稳定极限电压的临界点问题。在电网正常运行时,负荷缓慢增加导致负荷端母线电压缓慢下降,在到达运行极限之前,电压仍能维持稳定。而在到达电力系统承受负荷增加能力的临界值或接近临界值时,如果有扰动使系统状态越出临界值,如继续增加负荷、系统故障、甚至系统运行的正常操作,都将使负荷母线电压发生不可逆的突降。由于在不可逆的电压跌落之前电压并无明显变化,这种电压稳定丧失不易被运行人员觉察。
(2)动态电压稳定
电力系统是一个动态系统,并不总是单独地发生电压崩溃。电力系统动态稳定研究的是系统受到干扰后,不发生振幅不断增大的振荡而失步。电力系统发生故障后,为保证其功角暂态稳定及维持系统频率,常进行自动切机切负荷等操作。因为此时系统结构变得脆弱及系统电源支持负荷的能力变弱,在故障后的发电机快速启动、再同步并列、输电线重新带电、负荷再供电、电力系统解列部分再同步运行的恢复过程有可能导致电压失稳。
(3)暂态电压稳定
电力系统暂态稳定一般指的是受到大干扰后,各发电机保持同步运行并恢复到原先的或过渡到新的稳定运行状态的能力,通常是指第一摆或第二摆不失步。电力系统发生故障或受到其他类型的大扰动后,有可能出现某些负荷母线电压不可逆的突然下降,而此时发电机之间的相对摇摆可能未达到使电力系统功角失稳的程度。
目前电压崩溃机理没有统一的结论,对于电压崩溃现象主要有P-U 曲线、无功功率平衡、有载调压开关OLTC负调压作用和同步电机等多种解释。
为了便于研究分析,与功角稳定性类似,常将电压稳定性细分为小干扰电压稳定性和大干扰电压稳定性:
(1)小干扰电压稳定性,是指在遭受小干扰后,不发生自发振荡或非周期性失步,自动恢复到起始运行状态的能力,反应了系统控制电压的能力。这种稳定性主要取决于系统的负荷特性、各种连续控制和指定时刻的离散控制。
通常情况下,系统中的每个母线电压幅值随着注入该母线无功功率的增加而升高,假如有至少一个母线电压幅值随着注入该母线的无功功率的增加而降低,则认为该系统是电压不稳定的。即如果所有母线的V-Q灵敏度为正,则系统是电压稳定的;而如果有至少一个母线的V-Q灵敏度为负,则该系统是电压不稳定的。
(2)大干扰电压稳定性是指系统遭受大扰动(例如故障、线路跳闸等)后维持稳态电压的能力。对于给定的干扰和随后的系统控制措施,如果系统中所有母线的电压能够保持在可以接受的水平,我们就说系统是大干扰电压稳定的。系统在遭受大干扰后的电压失稳,既可以是由于快速动态负荷变动引起的短期电压失稳,也可以是慢速设备如有载调压、发电机励磁限制等引起的长过程电压失稳。
2 静止无功补偿器的工作原理
SVC在电力系统中可以发挥多种作用: SVC应用在系统侧能够提升稳态输送容量、电压稳定极限、暂态稳定性,还可以通过附加控制增强系统阻尼从而抑制同步振荡及提高高压直流输电系统的动态性能;SVC在用户侧可抑制电压波动和闪变、补偿三相不平衡、提高功率因数。
SVC有多种结构,常见的TCR装置的组成和工作原理如图1所示。
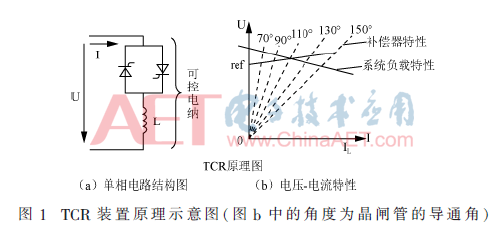
TCR装置的基本结构原理是晶闸管反并联后与电抗器串联,利用晶闸管的导通与关断来控制电抗器是否投入。在电源电压的正负半周,反并联的晶闸管轮流工作导通,当晶闸管的控制角α在90°~180°之间调节时,晶闸管受控导通(控制角为90°时完全导通,180°时完全截止关断)。若电网电压基本不变,在此范围内增大控制角将减少电抗器在一个周期内投入的时间,减少TCR支路的等效电流,从而减小感性无功功率;反之,减小控制角将增加电抗器在一个周期内投入的时间,增大TCR支路的等效电流,从而增大感性无功。其电压-电流特性曲线如图1(b)所示,图中每条曲线对应在导通角为某一特定角度下的伏安特性。如果仅考虑电流的基波分量,晶闸管反并联后与电抗器串联相当于一个可调电纳。其等效电纳为:

其中α为晶闸管触发角,L为电抗器电感值,ω为电网电压的角频率。
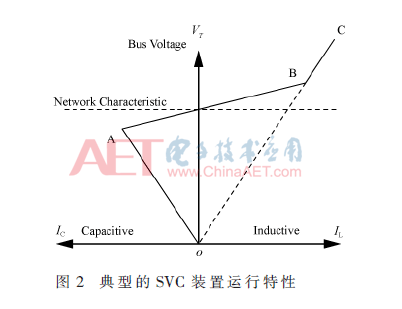
典型的SVC装置可以用固定电容器(FC)与可变电抗器的并联支路来表示,其V-I特性曲线如附图2所示,OA段对应电抗器取最小值,SVC相当于一固定电容器;BC段对应电抗器取最大值,SVC相当于一固定电抗器;AB段属于电抗器的调节区,SVC相当于一可变电纳,其斜率取决于控制系统。A点对应SVC的容性无功功率额定值,B点对应SVC的感性无功功率额定值。
3 含SVC的小扰动稳定性分析
近来电力系统运行日益接近稳定极限的情况下小干扰对电力系统影响越来越不可忽视。小扰动稳定性是指系统运行于某一稳态时,经受小扰动后能恢复到原状态,或接近扰动前可接受的稳定运行状态的能力。小扰动稳定分析用线性化的方法来研究,主要内容包括稳定性分析方法、稳定极限和特征值灵敏度分析等。
对于一个运行在稳态的网络,写成分块矩阵的形式


显然,如果存在一个或更多个实部为正的特征值,系统电压将会失稳。
与这些特征值对应的节点就是系统的薄弱点,在相应的节点上加入SVC后,向系统注入无功功率,则有可能将特征值的实部变为负的,从而使系统变为稳定。
4 结论
(1)SVC通过向系统注入动态无功,可以提高系统的小扰动电压稳定性。
(2)在小扰动稳定性分析中可以推导出系统中某些节点是电压稳定的薄弱点。
(3)系统中局部电压失稳对应的节点的特征值含有正实部,在相应节点安装SVC后,注入动态无功功率,有可能将对应的特征值实部变为负的,从而使系统变为稳定。
(4)推导出了一种选择电网局部薄弱点安装SVC的选择方法。
参考文献
[1] LI Peng,YU Yixin,JIA Hongjie,et a1.A study on boundary of small disturbance stability region[C].IEEE International Conference on Power System Technology,Kunming,China,2002.
[2] CANIZARES C A , FAUR Z T. Analysis of SVC and TCSC Controllers in voltage collapse[J]. IEEE Transactions on Power Systems, 1999, 14 (1) : 158-165.
[3] HISKENS IA , MCLEAN C B. SVC behavior under voltage collapse conditions[J]. IEEE Transactions on Power Systems, 1992, 7 (3) : 1078-1087.
[4] CIGRE Task Force 38. 05. 04, “Analysis and optimization of SVC use in transmission systems”. CIGRE Technical Brochure , No. 77 , 1993.
[5] VASCONCELOS A. N, RAMOS A. J . P, MONTEIRO J . S., et al. Detailed modeling of an actual static var compensator for electromagnetic transient studies[J]. IEEE Transaction on Power Systems, 1992, 7(1): 11 - 19.
作者信息:
喻 寻,顾 健,王映祥
(贵州电网有限责任公司毕节供电局,贵州 毕节 551700)

