0 引言

    短波频段由于电离层极化效应，使得阵列接收站可以同时接收水平和垂直极化2种分量，水平极化定向天线具有更好的灵敏度与更强的指向性，同时利用水平极化定向天线对常用垂直极化干扰具有较好的极化隔离作用，使得接收整体底噪较低。单个定向天线视角范围较小，将定向天线组成圆形天线阵，实现水平360°视角内信号的有效接收^[1]。目前还存在一些难题：(1)接收交叉极化会干扰甚至破坏接收信号中包含的来波方向信息^[2]；(2)短波对数周期天线、鱼骨天线等不存在固定的相位中心；(3)短波水平极化天线空间架设时水平展开出现了严重互耦现象。这些原因都使得阵列流型复杂多变，无法确定建模。基于水平极化定向天线阵列的短波测向算法虽然也采用了各种极化阵列自适应处理方法^[3-4]，但还是存在着测向游动较大的突出缺点，基于定向天线阵先测向再波束合成的算法在实际应用中有较大局限性，需要重点考虑自适应数字波束形成算法。

    对于经典自适应数字波束形成算法而言，非盲数字波束形成算法主要有最小均方误差算法(Minimum Mean Square Error，MMSE)、采样协方差求逆算法(Stimulate Matrix Inversing，SMI)、最小方差无失真响应算法(Minimum Variance Distorionless Response，MVDR)、线性约束最小方差算法(Linearly Constrained Minimum Variance，LCMV)、对角加载算法(Diagonal Loading，DL)、特征结构类算法(Eigenspace-Based，ESB)、零点预处理算法等。盲数字波束形成算法主要有循环自适应波束形成类(Cyclic Adaptive Beamforming，CAB)、最小二乘恒模算法(Least Square Constant Modulus Algorithm，CMA)、基于高阶累积量的联合近似特征矩阵对角化算法(Joint Approximate Diagonalization of Eigenmatrix，JADE)、基于独立分量分析的快速分离算法(FastICA)等^[5-6]。

    由于短波水平极化定向天线阵列流型未知，通常考虑应用盲数字波束形成算法。恒模算法由于具有较强的干扰抑制能力、对阵列幅相误差不敏感等优点，迭代运算不破坏相位信息，对后续的数字解调具有重要意义。恒模算法对于强信号的合成效果好，但是弱信号的合成效果较差，会出现错误捕获现象，需要进一步寻找有效方法提高算法的稳健性^[7-9]。如针对对数周期天线阵的一种盲波束形成算法，在最小二乘恒模算法基础上构造对角加载的初始权值来提高算法稳健性，算法主要考虑单个对数周期天线阵列流型的失配情况，未考虑大型方向性天线阵的交叉极化和互耦的实际影响。

    可以考虑跳出估计准确阵列流型的思路，建设2个异构阵列，1个垂直极化全向天线阵先用于测向，测向后可有效提取期望信号；1个水平极化定向天线阵直接用于高增益数字波束形成，相互协同更好地接收处理信号。同时考虑实际通信中常见的多径效应，如果处理不好会严重影响接收效果。另一个角度来看其实各径信号也包含了发射信号的波形信息，最佳接收端处理应充分利用各径的能量合并，相关文献提出了基于矩阵重构的多径接收鲁棒波束形成算法，但在定向天线阵中应用受限。

1 窄带多径环境下短波定向天线阵的数字模型

    短波M阵元接收阵列，假设空间中存在一组P个不同来向的多径信号，空间中还存在Q个独立或者多径的干扰信号，接收信号可写为：

    如果多径时延τ_p比较小或者信号带宽比较窄，记为窄带多径模型接收信号X(t)表示为：

    MMSE波束形成器无需知道信号阵列流型，关键问题就是如何获取期望信号波形。

2 自适应加载投影反馈的多径增强波束形成算法

    针对获取预知期望信号波形的问题，本文设计了短波多极化异构阵列协同处理方案，如图1所示，异构阵列流型不同，接收期望信号波形是相同的。

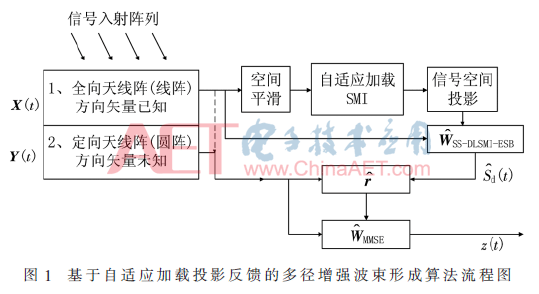
    由于全向天线阵接收信号也包括多径信号，需要首先进行去相关处理。下面以空间平滑(spatial smoothing)^[10]为例，均匀线阵的流型矢量可表示为：

    估计的期望信号含有噪声分量会影响最终波束形成效果，可以采用信号加干扰子空间来抑制噪声影响，即特征空间类算法[11]。

    各种非理想环境下得到波形信息后就可以利用MMSE波束形成器，具体又分2种情况：

    (1)短波同构阵列(即短波垂直极化全向天线阵)MMSE波束形成器的权值为：

    (2)短波异构阵列(即短波水平极化定向天线阵)MMSE波束形成器的权值为：

    当然，具体实现过程中也可以研究算法和速率损失较小情况下的低复杂度波束合成算法^[12]。

3 算法仿真与性能分析

3.1 实验1：自适应数字波束形成算法的方向图

    20元均匀直线阵，间距波长比为0.5，1个期望信号2条多径，角度为[80°，50°]，信噪比为0 dB；1个干扰2条多径，角度为[120，150°]，信噪比为10 dB；快拍数为1 000点。主径与反射径之间的复包络向量默认为[1，-0.5+0.5j]，空间平滑子阵数量为10。

    结论1：MMSE算法是已知期望信号波形信息，实现2径能量合并。如图2所示，SS-SMI-MMSE算法没有任何幅相差情况下只形成一个准确80°主瓣，主瓣比较宽，50°没有形成主瓣；如图3所示，有一定幅相差情况下，主瓣方向还发生偏离，算法性能下降。SS-DLSMI-ESB-MMSE算法在有无幅相差情况下都能很好地逼近理想MMSE算法。

3.2 实验2：同构阵列输出SINR与输入SNR关系

    阵列仿真条件与实验1相同，信噪比从-20 dB～30 dB变化，进行100次Monte-Carlo统计实验。

    结论2：在没有幅相差的情况下，各算法性能相当，同构阵列时ESB投影抑制了噪声分量，所以输出信干噪比更高；如图4所示，在有幅相差的情况下，SS-SMI-MMSE算法和SS-SMI-ESB-MMSE算法由于期望信号分量较大使得出现信号对消现象，输出性能下降；对角加载SS-DLSMI-ESB-MMSE算法克服了这个问题，但是自适应对角加载之后整体输出信干噪比略低于理想MMSE值；本文算法自适应设计加载量，保证性能与稳健性的平衡处理。

3.3 实验3：同构阵列输出SINR与角度误差关系

    阵列仿真条件与实验1相同，期望信号角度误差3°以内，进行100次Monte-Carlo统计实验。

    结论3：如图5所示，SS-SMI-MMSE算法、SS-SMI-ESB-MMSE算法和SS-DLSMI-ESB-MMSE算法的输出信干噪比都随着期望角度误差变大而降低，理想MMSE与角度估计精度无关，但是SS-DLSMI-ESB-MMSE算法的抗角度误差能力强。

3.4 实验4：异构阵列输出SINR与输入SNR关系

    阵列仿真条件与实验1相同，信噪比从-20 dB～30 dB变化，进行100次Monte-Carlo统计实验。

    结论4：如图6所示，有幅相差情况下，SS-SMI-MMSE算法与SS-SMI-ESB-MMSE算法性能一致，因为异构阵列的噪声本身也不相关，ESB投影抗噪处理不影响算法性能；但是SS-DLSMI-ESB-MMSE算法因为自适应加载，使得协方差矩阵减少了期望信号分量，输出信干噪比逼近理想MMSE性能。

3.5 实验5：异构阵列输出SINR与角度误差关系

    阵列仿真条件与实验1相同，期望信号角度误差3°以内，进行100次Monte-Carlo统计实验。

    结论5：如图7所示，SS-SMI-MMSE算法、SS-SMI-ESB-MMSE算法和SS-DLSMI-ESB-MMSE算法的输出信干噪比都随着期望角度误差变大而降低，理想MMSE与角度估计精度无关，SS-SMI-ESB-MMSE算法和SS-DLSMI-ESB-MMSE算法的性能相当，比SS-SMI-MMSE算法性能好，原因在于ESB处理还改善了期望角度误差。

3.6 实验6：算法在短波某实际系统中的应用验证

    短波24元水平对数周期天线组成圆阵接收实际信号，选取实际某天波信号进行应用验证，信号取大致来波方向的相邻7~10幅天线，通过观察可知多副天线的接收信号差异波动较大。

    结论6：如图8～图10所示，单个定向天线接收时两个信号时频混叠，基于自适应加载投影的多径增强波束形成算法可以稳健地分离出多信号，验证了算法的有效性。

4 结论

    本文分析了垂直极化全向天线阵与水平极化天线阵的优缺点及其应用场合，设计了一种短波多极化异构阵列协同处理方案，提出了基于自适应加载投影反馈的多径增强波束形成算法。该算法在已知期望信号大致度角的前提下，综合利用空间平滑、采样协方差矩阵求逆和空间投影等方法来估计波形，同时针对弱信号性能差的问题，通过自适应加载进一步提高波形估计的稳健性，算法计算简便，所需先验信息少，非理想条件适应性强。后续研究应该继续考虑水平极化定向天线向垂直极化全向天线的引导协同处理，提高微弱信号的测向问题。

参考文献

[1] 吴世龙.短波对数周期天线及其阵列的方向性[J].舰船电子工程，2004，142(4)：95-98.

[2] 曹倩，金元松.短波水平极化测向中的交叉极化波[J].电波科学学报，2009，24(4)：672-675.

[3] 胡显智，王宁，戴旭初.基于流行分离技术的DOA和极化参数联合估计方法[J].测试技术学报，2018，32(5)：72-79.

[4] 任晓飞，龚书喜，何绍林.水平对数周期天线空域极化[J].电波科学学报，2018，33(4)：429-435.

[5] TREICHLER J R，AGEE B G.A new approach to multipath correction of constant modulus signal[J].IEEE Transactions on ASSP，1983，31(4)：459-472.

[6] SHYNK J J，GOOCH R P.The constant modulus array for cochannel signal copy and direction finding[J].IEEE Transactions on SP，1996，44(3)：652-660.

[7] SIMANAPALLI S，KAVEH M.Broadband focusing for partially adaptive beamforming[J].IEEE Transactions on Aerospace and Electronic Systems，1994，30(1)：68-80.

[8] 张琦，唐斌.一种稳健自适应多波束形成算法[J].信号处理，2018，34(1)：13-19.

[9] 方玉河，李哲，曹永兴.基于导向矢量扩维的稳健波束形成方法[J].南京理工大学学报，2018，42(6)：722-726.

[10] 任全会，陈享成.低信噪比下相干信号DOA估计算法研究[J].电子技术应用，2018，44(11)：59-62.

[11] Wang Cheng，Tang Jun.Feedback beamforming technique for receiving multipath coherent signal[J].Multidimentional Systems and Signal Processing，2017，29(4)：1449-1457.

[12] 周应超，黄琼，申滨.基于内波束干扰消除的大规模MIMO低复杂度波束成形[J].电子技术应用，2017，43(8)：16-20.

作者信息:

唐  涛1，马  欢2，吴志东1

(1.信息工程大学，河南 郑州450001；2.同方电子科技有限公司，江西 九江332007)