0 引言

    众所周知，人们需要对数字图像中的隐私信息进行保护或加密，由于混沌系统具有拓扑传递性、正的李雅普诺夫指数并且对初始条件高度敏感，在数字图像混沌加密中获得了广泛的应用^[1-3]。例如，文献[4]利用Arnold映射置乱图像像素位置，文献[5]给出了一种基于DNA序列的加密算法，文献[6]介绍了一种基于Logistic映射的混沌加密算法，文献[7]给出了基于通信编码序列与多混沌图像加密算法，文献[8]给出了复合级联混沌的彩色图像加密算法，文献[9]给出了图像全息数字水印算法，文献[10]给出了基于DNA序列操作的新型混沌图像加密方案。还有最新的图像加密算法，如文献[11]给出的基于并行计算系统的快速图像加密算法。在这些算法中，例如文献[5]的密文直方图不均匀，文献[6]存在混沌范围小的特点等，此外部分算法存在混沌系统和加密算法与明文无关、用于生成混沌序列的混沌系统结构相对简单的不足。

    为解决上述问题，本文提出了一种基于三维Logistic-Sine级联映射(3D-LSCM)的图像混沌加密算法，将Logistic映射的输出作为Sine映射的输入，构造一种三维Logistic-Sine级联映射，在此基础上，利用3D-LSCM设计图像混沌加密算法。该算法的主要特点是采用两轮置乱和双向扩散的方法，并且将明文信息作为初始条件的一部分，增强等价密钥破译难度，最后给出了等价密钥分析、差分分析、相关性测试、密钥敏感性测试、密钥空间大小的结果。

1 3D-LSCM混沌映射的构造

    Logistic映射的数学表达式为：

    由于Logistic映射范围较小，只有当μ∈4时才出现单位区间[0，1]上的满映射；而Sine映射存在与Logistic映射一样的缺点，即具有有限的混沌映射范围和分布不均匀性。但如果将Logistic映射与Sine映射进行级联，则能扩大混沌映射的范围。基于上述考虑，本文在文献[12]的基础上，提出一种3D-LSCM映射，其迭代方程的数学表达式为：

    在式(3)中，Logistic映射的输出作为Sine映射的输入，进而由一维扩展到三维。与单独的Logistic映射和Sine映射相比，由于Logistic映射和Sine映射相互嵌套和耦合，因而具有更好的统计性能^[13]。李氏指数(Lipschitz Exponent，LE)计算结果如图1所示，可知3D-LSCM在整个控制参数区间内具有3个正的李氏指数(λ₁、λ₂、λ₃)。

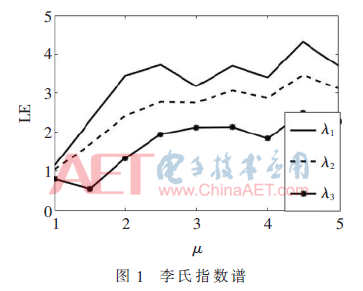
2 图像混沌加密算法

2.1 混沌加密流程图

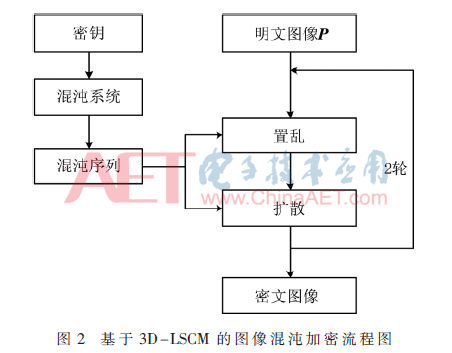
    本文设计了一种基于3D-LSCM的图像混沌加密算法，其流程图如图2所示。由图2可知，该算法采用了两轮置乱-双向扩散结构，密钥由x₀、y₀、z₀、μ组成，其中x₀、y₀、z₀为3D-LSCM的初始值，并且与明文相关；μ为3D-LSCM的控制参数。混沌序列则由3D-LSCM产生，主要用于两轮置乱-双向扩散中。设明文图像P的尺寸为M×N，对其混沌加密的流程图如图2所示。

2.2 初始值设置与混沌序列的生成

    为了抵御选择明文攻击，混沌系统的初始条件需要对明文有高度敏感性。为了解决这个问题，在本算法中，对初始值设置的数学表达式为：

其中，x、y、z是混沌系统产生的随机混沌序列，S是量化后的混沌序列，mod为取模运算。在本文中共用到3个混沌序列，即S₁、S₂、S₃。

2.3 加密与解密过程

    在本节中，图像混沌加密算法包括两轮置乱加密和双向扩散加密。其中双向扩散保证在密钥数量少的情况下仍然具有较好的安全性^[14]，解密过程为加密过程的逆运算。

2.3.1 第1轮置乱

    在置乱阶段利用Arnold Cat映射，其迭代方程的数学表达式为：

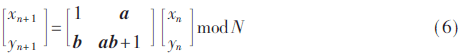
式中，a、b是猫映射的两个参数，其中a=S₁，b=S₂，(x_n+1，y_n+1)为坐标(x_n，y_n)处的像素被置乱后的位置。通过此轮置乱得到置乱图像，将其按照光栅方式扫描转换为一维序列R。

2.3.2 第1轮扩散

    本轮扩散环节采用异或双向扩散，即正向和逆向各一次。明文、密文和密钥三者相互异或，得正向扩散加密算法的数学表达式为：

2.3.3 第2轮置乱

    首先将第一轮扩散得到的一维扩散序列C_i转化为二维灰度图像，再通过Arnold Cat映射进行第二次置乱，将置乱后的图像按照光栅方式扫描转换为第二轮置乱后的一维序列E_i。

2.3.4 第2轮扩散

    本轮扩散通过采用取模双向扩散来改变像素值，得正向扩散加密的数学表达式为：

3 图像混沌加密数值仿真实验及安全性能分析

3.1 图像混沌加密数值仿真实验

    采用标准测试图像进行混沌加密数值仿真实验。实验平台主要包括 Windows 10操作系统、Intel Core^TM i7-5500U 2.4 GHz处理器、8 GB内存、1T硬盘、MATLAB 2015b。设密钥参数为x₀=0.01，y₀=0.2，z₀=0.16，μ=0.08。下面分别以图像大小为M×N=256×256的Lena、Baboon、Pepeers为例，进行图像混沌加密数值仿真实验，结果如图3所示。

3.2 密钥空间分析

    一个良好的图像加密系统必须具备足够大的密钥空间来抵御针对密钥的穷举攻击，当密钥空间大于2¹⁰⁰才能为加密系统提高安全可靠的保障^[15]。加密算法的密钥x₀、y₀、z₀、μ为双精度浮点数，计算精度为10^-14，密钥空间可达到10¹⁴×10¹⁴×10¹⁴×10¹⁴≈2¹⁸⁶>>2¹⁰⁰。

3.3 敏感性分析 

    一个好的加密算法要对密钥敏感。由加密算法可知，密钥参数为x₀、y₀、z₀、μ。保持其中3个不变，将x₀改变为x₀+10^-17时，可以解密出明文图像，而将x₀改变为x₀+10^-16时，无法解密出明文图像。对其余密钥参数的敏感性测试也有相似的结果。这都说明了该算法具有良好的密钥敏感性。

3.4 直方图分析

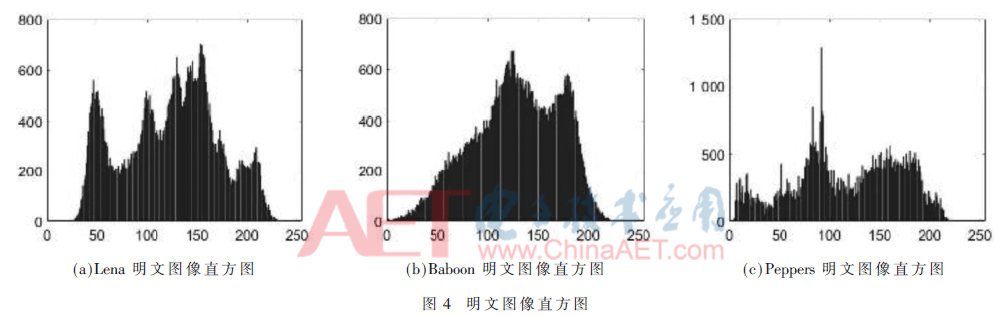
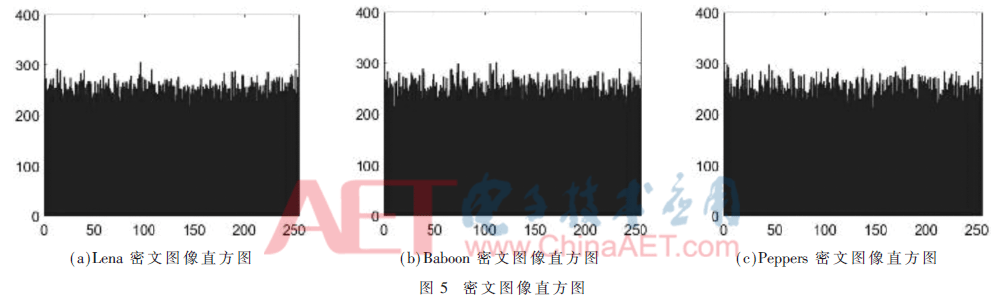
    一个好的加密算法得到的密文，其统计特性必须尽可能接近均匀分布，攻击者无法从密文统计特性中得到任何关于明文的有效信息，因而可以抵抗唯密文攻击。下面从明密文图像的统计直方图分析。

    由图4和图5可知，明文图像像素值的分布不均匀，密文图像像素值分布均匀，其中横坐标表示像素值，纵坐标表示相对应的出现频数。 

3.5 相邻像素相关性测试

    相邻像素的相关性一般从水平、垂直、对角线3个方向来体现。相关系数表示相邻像素之间的关系，相邻像素相关性越大，相关系数则越大^[16]。通过加密算法对像素进行置乱和扩散，破坏了像素之间的相关性，使得密文图像的相关系数接近0。相邻像素相关性测试的数学表达式为：

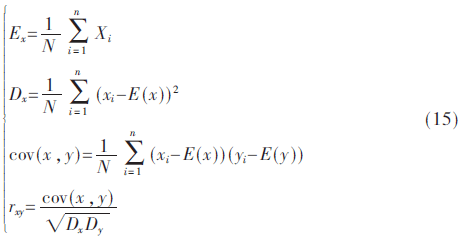
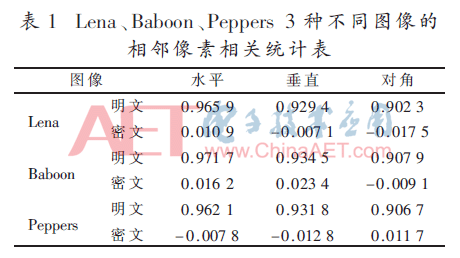
式中，x、y表示随机像素对的像素值，r_xy为随机像素对的相关系数。相邻像素相关统计的结果如表1所示，可知明文的相关系数都接近于1，说明明文像素之间有很高的相关性，而加密后的相关系数接近于0，说明密文之间不相关，能抵御统计攻击。表2还给出了与文献[8]和文献[15]的对比。由表2可知，本算法的密文图像相邻像素相关性更接近于0。

    Lena的明文和密文图像在不同方向上的相关性分布情况如图6所示，图6(a)、图6(b)、图6(c)(图6(d)、图6(e)、图6(f))横坐标都表示明文(密文)图像(x，y)处像素的灰度值，纵坐标分别表示明文(密文)图像(x+1，y)、(x，y+1)、(x+1，y+1)处像素的灰度值。由图可知Lena明文像素分布比较密集，基本都集中于y=x直线上，说明其相关性较强，而Lena密文图像像素分布于整个空间，说明密文不具有相关性。

3.6 差分分析

    差分分析主要是用来检验加密系统是否能够抵御差分攻击。差分攻击是指通过分析给定的明文与密文之间的差分关系，从而获得尽可能多的密钥，它能够用来攻击迭代次数少的密码^[17]。当两个明文图像仅存在一个像素不同时，假设密文图像第(i，j)点的像素值分别为C(i，j)和C′(i，j)，当满足C(i，j)=C′(i，j)时，D(i，j)=0；当C(i，j)≠C′(i，j)时，D(i，j)=1。其中C(i，j)、D(i，j)、C′(i，j)的定义分别为：

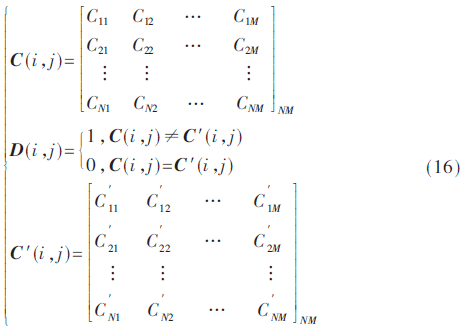
式中，M和N分别为图像的宽度和高度。

    通过引入图像像素值变化率(NPCR)和归一化像素值平均改变强度(UACI)两个指标来判断加密算法抵御差分攻击的能力。NPCR和UACI的定义为：

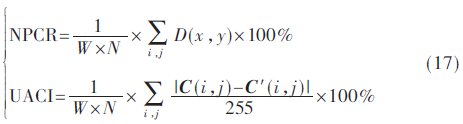
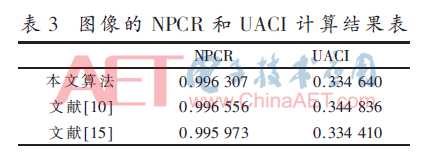
    通过测试，得到本文加密算法中NPCR=99.630 7%，UACI=33.464 0%。而已知NPCR和UACI的理想期望值为NPCR=99.609 4%和UACI=33.463 5%，表3是不同文献所对应的NPCR与UACI计算结果比较。从结果很明显可以看到本文测试数据与理想值非常接近，说明该混沌加密系统对明文变化非常敏感，明文对于密文存在雪崩效应，细小的明文变化会对密文产生较大的影响。

3.7 NIST测试

    一个序列是否达到信息加密的安全标准，需要对序列进行随机性测试。目前，大部分使用的是根据美国国家标准与技术研究院(NIST)提供的测试软件与标准。衡量随机性的方法是P-value方法，P-value是一个序列比真随机序列的随机性要好的概率。若被测试的100组106 bit序列的值满足，则通过测试，否则不通过。按照NIST测试软件的要求，选取100组长度为106 bit的加密序列进行测试，测试结果如表4所示。

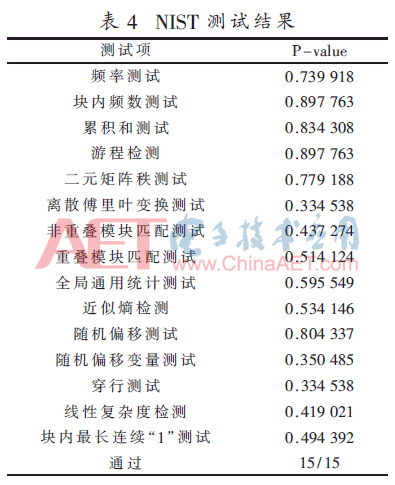
    由表4可知，加密序列通过了NIST全部测试，表明具有良好的随机特性。

3.8 选择明文攻击

    选择明文攻击：密码破译者不仅能够获得一定数量的明—密文对，还可以用他选择的任何明文，在同一未知密钥的情况下能加密得到相应的密文^[18]。

    对于“置乱—扩散”结构的图像混沌加密算法，选择明文攻击通常选择所有像素值相同的特殊明文图像使置乱操作失效，获取扩散等效密钥，进而获取置乱等效密钥，最终完成破译^[19]。为了抵御选择明文攻击，本文在加密过程中，使用式(4)将明文信息与初始值相结合，即使攻击者利用像素值全部相同的图像，也仅可以使第一轮的置乱过程无效，而第二轮置乱加密对于经过第一轮扩散的中间密文图像依旧有效。因此，攻击者无法通过选择的明文图像恢复未知随机序列。此外，即使攻击者得到对应某一像素值之和的所有等效密钥，也仅有1/(M×N×2⁸)的概率适用于待破译密文，故无法还原对应明文图像。

4 结论

    本文提出了一种基于3D-LSCM的图像混沌加密算法，该算法的主要特点是采用两轮置乱和双向扩散的方法，并且将明文信息作为初始条件的一部分，增强等价密钥破译难度，并给出了差分分析、相关性测试、密钥敏感性测试、密钥空间大小的结果。

参考文献

[1] 曹光辉，李春强.联合空域和小波域的图像加密[J].计算机应用，2017(2)：201-206.

[2] 禹思敏，吕金虎，李澄清.混沌密码及其在多媒体保密通信中应用的进展[J].电子与信息学报，2016，38(3)：735-752.

[3] 凌大旺，禹思敏.基于嵌入式系统的混沌数字图像加密研究[J].电子技术应用，2012，38(3)：20-22.

[4] GUAN Z H，HUANG F，GUAN W.Chaos-based image encryption algorithm[J].Physics Letters A，2005，346(1-3)：153-157.

[5] LIU H，WANG X，KADIR A.Image encryption using DNA complementary rule and chaotic maps[J].Applied Soft Computing，2012，12(5)：1457-1466.

[6] 洪媛，徐宁，涂兴华.基于Logistic混沌的图像实值加密[J].量子电子学报，2018，35(2)：149-155.

[7] 杨晓刚，刘国荣，毛彦斌.基于通信编码序列与多混沌图像加密算法[J].计算机应用与软件，2016(7)：304-307.

[8] 谢国波，朱润盈.复合级联混沌的彩色图像加密算法[J].计算机工程与应用，2018，54(8)：189-194.

[9] 胡广平，周华强.基于Lab空间的图像全息数字水印算法[J].电子技术应用，2014，40(4)：59-62.

[10] WANG X Y，ZHANG Y Q，BAO X M. A novel chaotic image encryption scheme using DNA sequence operations[J].Optics and Lasers in Engineering，2015，73：53-61.

[11] Wang Xingyuan，Feng Le，Zhao Hongyu.Fast image encryption algorithm based on parallel computing system[J].Information Sciences，2019，486：340-358.

[12] HUA Z，ZHOU Y.Image encryption using 2D Logistic-adjusted-Sine map[J].Information Sciences，2016，339：237-253.

[13] HUA Z，JIN F，XU B，et al.2D Logistic-Sine-coupling map for image encryption[J].Signal Processing，2018，149：148-161.

[14] 许爽，王伟，苏玉.基于双向扩散机制融合伪随机数同步生成器的快速图像加密算法研究[J].科学技术与工程，2014，14(7)：45-50.

[15] 徐扬，黄迎久，李海荣.一个切换Lorenz混沌系统在图像加密中的应用[J].包装工程，2018(5)：179-184.

[16] 张勇.混沌数字图像加密[M].北京：清华大学出版社，2016.

[17] OZKAYNAK F.Brief review on application of nonlinear dynamics in image encryption[J].Nonlinear Dynamics，2018，92(2)：305-313.

[18] 吴世忠，祝世雄，张文政.应用密码学：协议，算法与C源程序[M].北京：机械工业出版社，2014.

[19] ZHU C X，LIAO C L，DENG X H.Breaking and improving an image encryption scheme based on total shuffling scheme[J].Nonlinear Dynamics，2013，71(1-2)：25-34.

作者信息:

曾  珂，禹思敏，胡迎春，张泽清

(广东工业大学 自动化学院，广东 广州510006)