0 引言

    大数据处理项目中，资源消耗最为突出的是数据的收集和预处理，大约占项目资源支出的80%，其中数据预处理工作量就要占60%左右^[1]。究其原因，是因为实际应用系统收集数据时，由于数据源的区别、考虑因素不同及数据收集工具和数据传输问题等造成收集到的数据存在数据不完整、重要属性缺失、有噪声和数据不一致等问题。要得到高质量的决策，必然要求高质量的数据，所以数据预处理在数据分析工作量中占比最大，目的是给数据挖掘提供准确、一致、及时、权威的数据集。数据预处理工作包括缺失值（空值）处理、异常值处理、数据集成和数据规约，其中数据规约是影响大型数据集预处理效果的主要瓶颈。文献[2]中提出基于聚类方法实现数据分层；文献[3]-[4]中提出离群值检测进行异常值处理，进而数量规约；文献[5]-[6]中提出基于相似连接实现数据并行处理；文献[7]-[9]提出了选用二维离散小波进行维度规约的数据预处理；文献[10]-[11]提出了针对稀疏数据进行数量规约的方法。而针对存在相关性的多个变量，目前广泛使用主成分分析(Principal Component Analysis，PCA)方法进行降维，从而使用较少的综合指标来代表原变量中的各类信息，降低数据分析的复杂性。

1 主成分分析PCA

    PCA的思想是将n维特征映射到k维(k<n)全新的正交特征(即主成分)上^[12]。其算法描述为：

    (1)输入：n维特征数据集；

    (2)计算样本均值：

    (3)计算样本方差S²：

    (7)得到降序排列的前k个λ_i对应的特征向量z_i组成的矩阵；

    (8)输出：转换到k个特征向量构建的新空间数据集。

    由算法描述可知，PCA方法即通过基变换实现降维。为了保证最优变换，PCA采用最大方差来确保基保留信息量的最大化。

    使用PCA方法进行数据维规约时，计算易于实现，只需要考虑原数据集的协方差矩阵大小，且k个主成分各自独立^[13]。但PCA方法降维后，主成分的各个特征解释性有所降低，而且未被选择的非主成分也可能含有对样本差异的重要信息，从而造成新的数据不完整。

2 改进的PCA数据预处理方法

    使用PCA方法进行维规约时，首先需要对原数据集中的数据中心化，其后也没有人为设定参数或参照经验模型进行计算，从而保证结果和数据相关，且独立于用户^[14]。由于均值易受极端值影，简单地使用与均值相减实现数据中心化是造成映射所得主成分的特征解释性降低的原因之一。为了解决这一问题，在对数据中心化时，用加权规范化均值来代替均值实现数据中心化。加权规范化均值计算公式为：

其中，I_d为数据集中的元素，d为元素与均值差，w_d为每个元素对应d所分配的权值，满足∑w_d＝1。

    改进后的PCA算法描述为：

    (1)输入：n维数据集X={x₁，x₂，…，x_n}；

    (5)计算目标函数，其中v为单位向量：

    (6)得到max(f(v))的必要条件为Cv=λv，则v为协方差矩阵的特征向量，其保存的信息量为特征值λ；

    (7)将协方差矩阵C对角化，得到n个不同的特征值λ_i，降序排列；

    (8)while(k<=n){

    (9)输出：映射到新基集的数据集。

3 算法验证实验

3.1 原始数据集概况

    实验采用的数据集为长江流域夹江扬州三江营点位南水北调东线取水口断面2018年52期水质自动监测数据共364条，水质监测指标包括PH值、溶解氧DO、高锰酸钾指数CODMn、氨氮 NH3-N、总磷TP、总氮TN和总有机碳TOC共7个变量，数据集片段如图1所示。

3.2 数据中心化处理

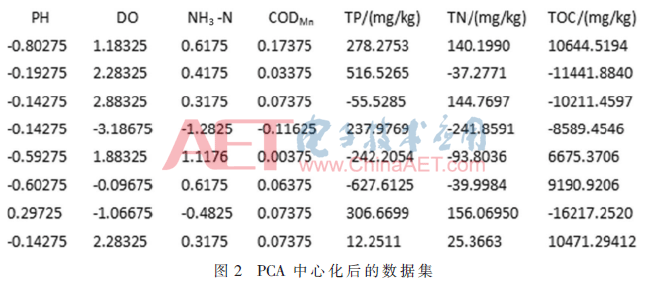
    PCA方法对每个特征变量求均值，即计算=xi-，得到中心化后的数据集片段如图2所示。

3.3 基于协方差矩阵的特征值确定主成分数量

    根据计算Rayleigh商和Cattell碎石检验原则，使用改进PCA方法前后，基于特征值对应的主成分选择如图4所示。

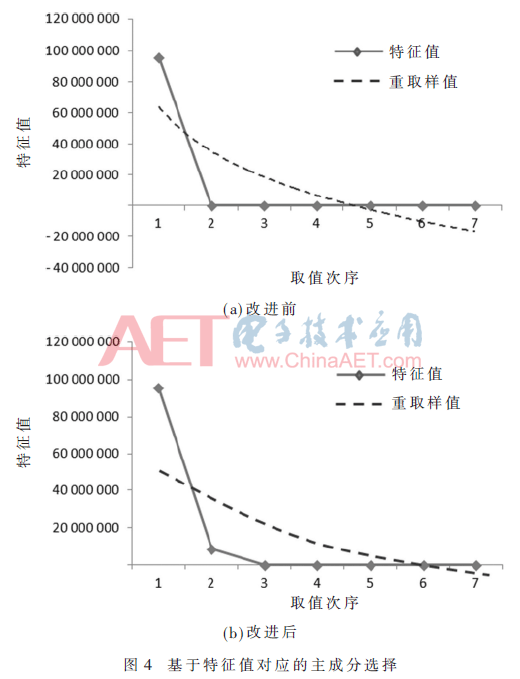
    由图4(a)可知，根据特征值对应选择第1、2、3和7个特征变量即可以表示数据集，数据集由346×7降为346×4，且变量TOC和CODMn、TN和NH3-N相关性较强，但注意到变量TP没有被解释。

    由图4(b)可知，根据特征值对应选择第1、2、3、4和7个特征变量即可以表示数据集，数据集由346×7降为346×5，且变量TOC和CODMn、TN和NH3-N相关性较强，可以进行合并，并且没有丢失变量TP的特征数据。

3.4 根据特征向量矩阵生成新数据集

    将特征值对应的特征向量构造矩阵，得到数据降维转换基，转换前后数据集特征值示意图如图5所示。

    由图5可知，使用PCA方法进行降维处理后，仍然可以保留原始数据集的大部分变量特征值，但实验证明改进后的PCA方法寻找主成分更为谨慎，对特征特征值描述更加清晰。

4 结论

    主成分分析(PCA)是通过正交变换将n个可能相关的变量转换为k个（k<n）不相关的变量，从而寻找到代表原数据集的主成分变量的一种统计方法，是目前使用最广泛的数据维规约算法。理想的PCA方法使用要求最大方差和最少非主成分数据丢失，故使用PCA方法时要关注生成的协方差矩阵质量和特征值的选取数量。中心化数据时将均值计算转变为加权规范平均值的计算，可以充分考虑各变量特征值的统计性能，保证生成的协方差矩阵质量。通过Rayleigh商和Cattell碎石检验原则可以选择更合理的特征值数目，尽可能避免出现非主成分含有对样本差异的重要信息丢失。实验结果表明，改进后的PCA算法更能保证数据完整性，虽然可能会降低维规约的效率，但数据完整是高质量的数据源首先应该考虑的。

参考文献

[1] 曾祥坤，张俊辉，石拓，等.基于主题提取模型的交通违法行为文本数据的挖掘[J].电子技术应用，2019，45(6)：41-45.

[2] 文若晴，马昂，潘晓.基于密度聚类的签到轨迹大数据分层预处理研究[J].计算机应用与软件，2019，36(3)：20-28.

[3] ZHANG Y，MERATNIA N，HAVINGA P.Outlier detection tech-niques for wireless sensor networks：a survey[J].IEEE Com-munications Surveys ＆ Tutorials，2010，12(2)：159-170.

[4] LEI P R.A framework for anomaly detection in maritime traj-ectory behavior[J].Knowledge and Information Systems，2016，47(1)：189-214.

[5] 郭方方，潮洛蒙，朱建文.基于相似连接的多源数据并行预处理方法[J].计算机应用，2019，39(1)：57-60.

[6] CHEN Y F，ZHAO X，HE P J，et al.BMGSJoin：a MapReduce based graph similarity join algorithm[J].Pattern Recognition & Artificial Intelligence，2015，28(5)：472-480.

[7] 张玺君，袁占亭，张红，等.交通轨迹大数据预处理方法研究[J].计算机工程，2019，45(6)：26-31.

[8] 崔光照，曹祥，张华.基于小波变换的基因表达数据去噪聚类分析[J].信号处理，2005，21(s1)：463-466.

[9] SU H，ZHENG K，WANG H，et al.Calibrating trajectory data for similarity-based analysis[C].ACM SIGMOD International Conference on Management of Data.ACM，2013：833-844.

[10] 李志平，付冬梅，穆志纯.基于稀疏数据规约的CMAC大气腐蚀数据补偿方法[J].计算机应用研究，2016，33(9)：2645-2647.

[11] TAGHAVIPOUR A，FOUMANI M S，BOROUSHAKI M.Implementation of an optimal control strategy for a hydraulic hybrid vehicle using CMAC and RBF networks[J].Scientia Iranica，2012，19(2):327-334.

[12] 范叶平，李玉，杨德胜，等.基于深度集成学习的人脸智能反馈认知方法[J].电子技术应用，2019，45(5)：5-8，13.

[13] 谢霖铨，徐浩，陈希邦，等.基于PCA的决策树优化算法[J].软件导刊，2019，18(9)：69-71，76.

[14] 张云龙.基于PCA的高维流式数据聚类算法[J].电子技术与软件工程，2019(8)：175-176.

作者信息:

陈  燕1，陈亚林2，郑  军1

(1.贵阳学院 数学与信息科学学院，贵州 贵阳550002；2.南京财经大学 管理科学与工程学院，江苏 南京210046)