文献标识码: A
DOI:10.16157/j.issn.0258-7998.191074
中文引用格式: 胡金艳,宋绍京. VPx帧内压缩的快速算法[J].电子技术应用,2020,46(4):75-78,88.
英文引用格式: Hu Jinyan,Song Shaojing. Fast algorithm for VPx intra-frame compression[J]. Application of Electronic Technique,2020,46(4):75-78,88.
0 引言
目前主流的视频编码标准包括3个体系:国际联合视频工作组(Joint Video Team,JVT)的H.26x、国内数字音视频编解码技术标准工作组(Audio Video Coding Standard,AVS)的AVSx和Google公司的VPx[1-4]。其中,VPx编解码器(COder/DECoder,CODEC)凭借开源和免专利费的优势,在全球范围内各种网络浏览器的支持率已经超过92%[5]。
视频编码标准中的帧内压缩是决定最终编码效率的关键,但由于该过程的算法复杂度高而导致非常耗时,因此对帧内压缩快速算法的研究显得尤为必要。近年来这方面的研究主要集中在H.264和H.265/高性能视频编码(High Efficiency Video Coding,HEVC)[6-9]。文献[6]通过统计方法与阈值法,文献[7]基于纹理方向检测,文献[8]利用时间与时空相关性,分别对HEVC帧内预测进行加速,实现将编码时间减少24~30%。文献[9]提出梯度法加快确定帧内模式,将编码时间减少15%,再结合支持向量机(Support Vector Machine,SVM)加快确定HEVC编码单元划分,使编码时间进一步减少到50%以上。文献[10]对HEVC和VP9两种标准的帧内压缩算法及其对编码效率的影响进行了比较。本文针对VPx的帧内压缩提出了加速算法,并通过实验验证了算法的效果。
1 VPx帧内压缩
帧内压缩是基于相邻像素之间的相关性,通过当前块的相邻块对其进行预测,并对预测值与实际值之间的残差进行一系列变换、量化和熵编码,以消除空间冗余达到压缩的目的。图1所示为VPx帧内压缩框图。VPx帧内压缩以宏块/超级块为单位,其中VP8标准的宏块大小为16×16,VP9标准的超级块大小为64×64。VP8采用4×4的子块划分方式将宏块划分为4×4大小的子块,其变换包括离散余弦变换(Discrete Cosine Transform,DCT)和沃尔什-哈达玛变换(Walsh-Hadmard Transform,WHT)。VP9采用四叉树子块划分方式将超级块划分为4×4~64×64大小的子块,其变换包括非对称离散正弦变换(Asymmetric Discrete Sine Transform,ADST)和DCT。
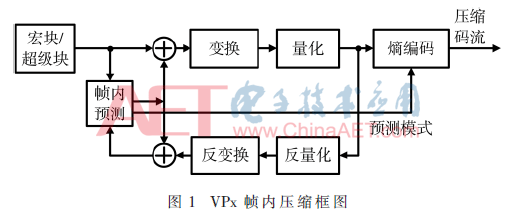
VPx帧内预测分为亮度块预测和色度块预测。亮度块预测包括以下10种预测模式:

其中,DC和TM分别为直流和真运动预测模式,另外8种为角度预测模式,图2中以4×4的亮度块预测为例说明。HE和VE分别为水平和垂直预测模式,LD和RD分别为45°和135°预测模式,VL和VR分别为63°和117°预测模式,HD和HU分别为153°和207°预测模式。

在帧内压缩过程中,要从上述10种预测模式中选择一种,使码率在不超过某最大码率的情况下失真最小。VPx采用率失真优化(Rate Distortion Optimization,RDO)方法来寻找码率和失真之间的平衡,其率失真代价函数表示为:

其中,Jmode为预测模式对应的率失真代价,Dmode为失真,λmode为拉格朗日系数,Bmode为所需比特数。通过计算预测残差的平方和(Sum Squared Error,SSE)得到失真Dmode。对于每个亮度子块,要进行10次变换、量化、反量化和反变换的重构过程,根据率失真代价Jmode最小的原则选取最终预测模式,进入熵编码。
假设帧内压缩图像宽度和高度分别为W和H,宏块/超级块大小为C×C,则总的宏块/超级块数为:

以1 280×720的图像为例,宏块大小为16×16,按4×4的子块划分方式,得到4×4的亮度子块,则RecCnt的理论值为576 000次,意味着如此大量次数的变换、量化、反量化、反变换和率失真计算代价。
2 快速算法
为减少帧内压缩的运算量,可以从两方面入手:一方面减少亮度子块的重构次数,另一方面优化帧内压缩的算法程序。下面主要讨论前者。
2.1 最近邻加速法
最近邻加速法利用当前子块与其最近邻子块的相关性,以最近邻子块的预测模式作为其最终预测模式,从而减少遍历预测模式带来的重构次数。
图3所示为将图像中一个16×16的宏块划分为16个4×4的亮度子块,虚线框表示当前子块,箭头所在子块表示其候选最近邻子块。

首先根据当前子块在宏块中的位置确定最邻近子块。设当前子块为Si,j,3个候选最近邻子块分别为Si-1,j、Si,j-1、Si-1,j-1。S1,1作为第一个子块,不存在最近邻子块。
将Si,j的最邻近子块定义为NBi,j,当候选最近邻子块仅存在于水平和垂直方向时,有:
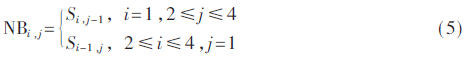
当候选最近邻子块存在水平、垂直和对角方向时,则先根据不同方向上子块的率失真代价从候选最近邻子块中确定最近邻子块:
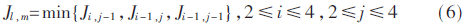
其中,Jl,m为3个方向率失真代价Ji,j-1、Ji-1,j、Ji-1,j-1中最小的,l和m代表最近邻子块的坐标。则有:

假设最近邻子块NBi,j的最佳预测模式为mode,对当前子块在该模式下进行重构和率失真Ji,j计算。当满足如下关系时,将模式mode作为当前子块的最终预测模式。

否则将对当前子块进行预测模式的遍历,得到最终预测模式。
在最近邻子块的判断过程中,要在当前宏块/超级块范围内,保存当前子块Si,j的前序子块的最佳预测模式和与其对应的率失真,用于与当前子块直接比较以简化率失真计算。 2.2 阈值加速法
对当前子块的率失真Ji,j设置阈值TH。当某一预测模式下的Ji,j满足如下关系时,终止对预测模式的遍历,将该预测模式作为当前子块的最终预测模式:

否则将继续进行下一个预测模式。如果所有预测模式对应的率失真均不满足式(9),则根据RDO原则选取最佳预测模式。
阈值的选取直接影响最终结果。阈值越大,越容易提前终止对预测模式的遍历,从而提高压缩速度,同时降低压缩质量;反之阈值越小,越难满足阈值要求,遍历的预测模式越多,从而保持压缩质量,但压缩速度提高少。式(10)给出了阈值选取公式:
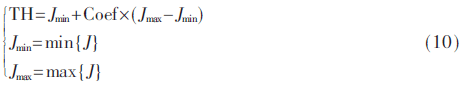
其中,J表示已有子块率失真的集合,Jmax和Jmin分别为J中的最大率失真和最小率失真,Coef取值0.062 5。
2.3 两级加速法
采用最近邻法加速时,如果当前子块存在最近邻子块,则能够减少子块重构运算量;否则仍需要对所有预测模式进行遍历。采用阈值加速法时,如果当前子块的率失真满足阈值条件,则能够减少子块重构运算量;否则仍需要对所有预测模式进行遍历。
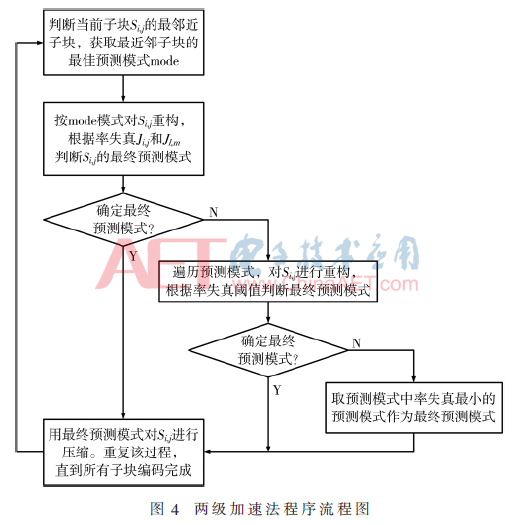
将上述两种加速方法结合,构成如图4所示的两级加速法,使帧内压缩速度进一步提高。两级加速法的第一级为最近邻加速,第二级为阈值加速。
3 实验结果与分析
为了验证算法的有效性,将本文算法在Google官方发布的libwebp-1.0.0上进行实现。该库利用VP8帧内压缩算法对WebP图像进行编解码。
实验的硬件环境:Inter-CoreTM i5-6200 CPU,主频为2.40 GHz,内存为4.00 GB,操作系统为64 位Windows 10。软件环境:Visual C++ 6.0。参数设置:品质因数(Quality factor)为80。选用源自Wikipedia的6张测试图像,如图5所示。这些图像涵盖不同的分辨率和内容复杂度。

对测试图像分别用原始方法、最近邻加速法、阈值加速法和两级加速法进行编码实验。表1所示为几种方法对应的单张图像子块重构数统计。可以看出,采用最近邻法和阈值法均使子块重构次数在一定程度上降低。对于图像Balloon,由于原图像较平坦,最近邻法得到的子块重构次数降低到原重构次数的1/3以下;而对于图像Boy,原图像具有较多细节,最近邻法得到的子块重构次数仅有少量降低。结合阈值法后,对于上述测试图像,通过两级法加速后得到的子块重构次数均大幅度减少。
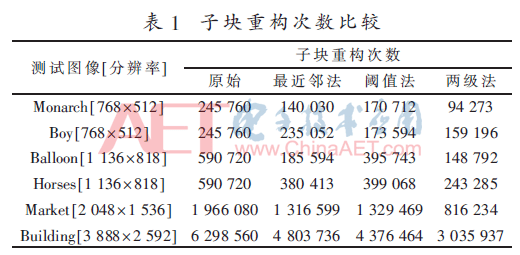
图6对几种加速方法从编码时间T、编码比特率BR和峰值信噪比PSNR 3个方面进行比较。可以看出对分辨率和内容不同的图像,帧内编码的时间都有大幅度降低,而BR和PSNR只有很小的变化。通过式(11)可以进一步得到上述算法的具体性能指标:

其中,ΔT表示所提出算法的编码时间减少的百分比,Torg和Tproposed分别为原始编码时间和所提出算法的编码时间;ΔPSNR表示PSNR减少的dB值,PSNRorg和PSNRproposed分别为原始编码的PSNR和所提出算法的PSNR;ΔBR表示BR增加的百分比,BRorg和BRproposed分别为原始编码的BR和所提出算法的BR。根据对测试图像的实验统计和计算结果,得到最近邻法的ΔT平均为37%,ΔBR平均为1%,ΔPSNR平均为0.06 dB;两级法的ΔT平均为49%,ΔBR平均为4%,ΔPSNR平均为0.14 dB。采用两级法加速时,图像Balloon加速最多,ΔT达到59%,对应编码质量ΔBR为6%,ΔPSNR为0.24;图像Boy加速最少,ΔT为41%,对应编码质量ΔBR为1%,ΔPSNR为0.07。
4 结论
为了降低VPx帧内压缩的计算复杂度,减少编码时间,本文提出了一种快速算法。实验结果表明:对于不同内容复杂度的图像,所提出的最近邻法在编码时间明显减少平均37%的情况下,对图像质量影响极小;基于最近邻法进一步提出的两级加速法在对图像质量影响很小的情况下,编码时间大幅度减少平均49%。进一步的优化工作包括子块划分、帧内压缩算法的软件优化和硬件加速。
参考文献
[1] SULLIVAN G J,OHM J,HAN W J,et al.Overview of the high efficiency video coding(HEVC) standard [J].IEEE Transactions on Circuits & Systems for Video Technology, 2012, 22(12): 1649-1668.
[2] 黄铁军.AVS2标准及未来展望[J].电视技术,2014,38(22):7-10.
[3] BANKOSKI J,WILKINS P,XU Y W.Technical overview of VP8,an open source video codec for the web[C].2011 IEEE International Conference on Multimedia and Expo,ICME′11.IEEE,2011:1-6.
[4] SRINIVASAN M.VP9 Encoder and decoders for next generation online video platforms and services[C].SMPTE 2016 Annual Technical Conference and Exhibition,SMPTE,2016:1-14.
[5] LI Z R,DUANMU ZH F,LIU W T,et al.AVC,HEVC,VP9,AVS2 or AV1?-A comparative study of state-of-the-art video encoders on 4K videos[C].Image Analysis and Recognition ICIAR 2019,Springer,2019,11662:162-173.
[6] 李伟,王让定,王家骥.一种HEVC帧内预测模式快速选择算法[J].计算机工程与应用,2016,52(14):161-166.
[7] RUIZ D,ESCRIBANO G F,MARTINEZ J L,et al.Fast intra mode decision algorithm based on texture orientation detection in HEVC[J].Signal Processing: Image Communication,2016,44:12-28.
[8] 谌博,顾梅花,马蒙蒙.一种改进的HEVC帧内预测算法[J].计算机与数字工程,2017,45(1):131-134.
[9] ZHANG T,SUN M T,ZHAO D,et al.Fast intra mode and CU size decision for HEVC[J].IEEE Transactions on Circuits & Systems for Video Technology,2017,27(8):1714-1726.
[10] SHARABAYKO M P,PONOMAREV O G,CHERNYAK R I.Intra compression effciency in VP9 and HEVC[J].Applied Mathematical Sciences, 2013, 7(137): 6803-6824.
作者信息:
胡金艳,宋绍京
(上海第二工业大学 计算机与信息工程学院,上海201209)

